Some non-convex quadratic models I
The new version of Gurobi v 9 introduced support for non-convex quadratic models. Cplex already supported some classes of such models (such as non-convex QPs). Here are just some models we can now try to solve with these solvers.
It is noted that you need to specify a solver option for Cplex and Gurobi to accept most non-convex models, Some models can be reformulated by the solver, but "real" con-convex models require the option OptimalityTarget 3 (Cplex) or NonConvex 2 (Gurobi).
It is noted that you need to specify a solver option for Cplex and Gurobi to accept most non-convex models, Some models can be reformulated by the solver, but "real" con-convex models require the option OptimalityTarget 3 (Cplex) or NonConvex 2 (Gurobi).
1a. Largest Empty Rectangle
Given is an area with \(n\) points:
The problem is to find the largest empty rectangle, i.e., without any points inside. The solution looks like:
The idea behind the model below, it that a data point \(p_i\) must be either left, right, below or above the rectangle. So it the coordinates of the rectangle are denoted by \(r_{x,lo},r_{x,up},r_{y_lo},r_{y_up}\), then at least one of the following constraints must hold: \[\begin{align} & p_{i,x} \le r_{x,lo} \\& p_{i,y} \le r_{y,lo} \\ & p_{i,x} \ge r_{x,up} \\& p_{i,y} \ge r_{y,up}\end{align}\] The complete mathematical model to find this rectangle can be stated as:
For the 2d case, the objective can be written as \[\min\> \mathit{area} = (r_{x,up}-r_{x,lo})\cdot (r_{y,up}-r_{y,lo})\] The outer area is a given rectangle with limits \(L_x, U_x, L_y, U_x\). I used here the unit box: \(L_x=L_y = 0\) and \(U_x=U_y = 1\). The big-M constants \(M_x, M_y\) need tight values. We can use the area dimensions for that. For a formulation without big-M constraints, we can implement implications using indicator constraints: \[\begin{align} & \delta_{i,c,lo}=1 \implies p_{i,c} \le r_{i,c,lo} \\ &\delta_{i,c,up}=1 \implies p_{i,c} \ge r_{i,c,up}\end{align}\]
The problem is not convex because of the objective. It is noted that we can simplify the objective a bit by writing \[\begin{align}\max\>&\mathit{area} = \mathit{side}_x \cdot \mathit{side}_y\\ & \mathit{side}_c = r_{c,up} - r_{c,lo}\end{align}\] This is a small problem with just 4 continuous quadratic variables and \(n\times 4\) binary variables. Gurobi or Cplex solve this model very quickly.
This problem can also be solved with available global solvers. Both Antigone and Baron have no problems with it. The optimal solution looks like:
I also tried the open-source solver Couenne. That was a surprise:
This is obviously a bad and non-optimal solution. I don't know what is going on here, but this looks like a bug.
It is easy to make a 3d version of the model above. Just replace \(c = \{x,y\}\) by \(c = \{x,y,z\}\). Unfortunately, there is one complication: now the model has an objective that is no longer quadratic. However, this can be fixed by chaining: \[\begin{align} \max\>&\mathit{volume} = \mathit{area}\cdot \mathit{side}_{z}\\ & \mathit{area} = \mathit{side}_{x} \cdot \mathit{side}_{y} \\ & \mathit{side}_c = r_{c,up}-r_{c,lo} && \forall c \end{align}\]
A solution can look like:
Note that Cplex can not handle this problem: Cplex allows non-convexities in the objective only (apart for some cases where it can reformulate things).
Here \(i\) indicates the point, \(i \in \{1,\dots,n\}\) and \(c\) is the coordinate. For a 2D problem, we have \(c \in \{x,y\}\).
When we use \(n=50\) random points, Gurobi is not able to even come close to proven optimality, I used a time limit of 2 hours, and the final gap is enormous:
Summary:
The big gap is partly due to the small best-found solution (0.01935). But mainly: this is a very difficult job for Gurobi. Even when the problem is relatively small: just 100 continuous variables,
By inspecting the solution, we see this solution is not very good at all:
I expect a much more regular pattern.
We can try to improve performance by noticing there is much symmetry in the model. The same solution can be obtained by just renumbering the points. To break symmetry, I added the constraint: \[\sum_c x_{i,c} \ge \sum_c x_{i-1,c}\] This was not very successful:
 |
| n=50 random points |
The problem is to find the largest empty rectangle, i.e., without any points inside. The solution looks like:
 |
| Largest empty rectangle |
The idea behind the model below, it that a data point \(p_i\) must be either left, right, below or above the rectangle. So it the coordinates of the rectangle are denoted by \(r_{x,lo},r_{x,up},r_{y_lo},r_{y_up}\), then at least one of the following constraints must hold: \[\begin{align} & p_{i,x} \le r_{x,lo} \\& p_{i,y} \le r_{y,lo} \\ & p_{i,x} \ge r_{x,up} \\& p_{i,y} \ge r_{y,up}\end{align}\] The complete mathematical model to find this rectangle can be stated as:
| Smallest empty rectangle |
|---|
| \[\begin{align} \max\> & \color{darkred}{\mathit{area}} = \prod_c (\color{darkred}r_{c,up}-\color{darkred}r_{c,lo}) \\ & \color{darkblue}p_{i,c} \le \color{darkred}r_{c,lo}+\color{darkblue}M_c(1-\color{darkred}\delta_{i,c,lo}) && \forall i,c\\ & \color{darkblue}p_{i,c} \ge \color{darkred}r_{c,up}-\color{darkblue}M_c(1-\color{darkred}\delta_{i,c,up}) && \forall i,c\\ & \sum_{c,s} \color{darkred}\delta_{i,c,s} \ge 1 && \forall i \\ & \color{darkblue} L_c \le \color{darkred}r_{c,lo} \le \color{darkred}r_{c,up}\le \color{darkblue} U_c \\ & \color{darkred}\delta_{i,c,s} \in \{0,1\} \end{align} \] |
| \[\begin{align} & i = \{1,\dots,n\}\\ & c = \{x,y\}\\ & s = \{lo,up\} \\ & \color{darkblue} L_c = 0 \\ & \color{darkblue} U_c = 1 \\ & \color{darkblue} M_c = \color{darkblue}U_c-\color{darkblue}L_c \end{align}\] |
For the 2d case, the objective can be written as \[\min\> \mathit{area} = (r_{x,up}-r_{x,lo})\cdot (r_{y,up}-r_{y,lo})\] The outer area is a given rectangle with limits \(L_x, U_x, L_y, U_x\). I used here the unit box: \(L_x=L_y = 0\) and \(U_x=U_y = 1\). The big-M constants \(M_x, M_y\) need tight values. We can use the area dimensions for that. For a formulation without big-M constraints, we can implement implications using indicator constraints: \[\begin{align} & \delta_{i,c,lo}=1 \implies p_{i,c} \le r_{i,c,lo} \\ &\delta_{i,c,up}=1 \implies p_{i,c} \ge r_{i,c,up}\end{align}\]
The problem is not convex because of the objective. It is noted that we can simplify the objective a bit by writing \[\begin{align}\max\>&\mathit{area} = \mathit{side}_x \cdot \mathit{side}_y\\ & \mathit{side}_c = r_{c,up} - r_{c,lo}\end{align}\] This is a small problem with just 4 continuous quadratic variables and \(n\times 4\) binary variables. Gurobi or Cplex solve this model very quickly.
This problem can also be solved with available global solvers. Both Antigone and Baron have no problems with it. The optimal solution looks like:
---- 50 VARIABLE area.L = 0.113 ---- 50 VARIABLE r.L coordinates of rectangle lo up x 0.403 0.792 y 0.285 0.575
I also tried the open-source solver Couenne. That was a surprise:
S O L V E S U M M A R Y
MODEL m OBJECTIVE area
TYPE MIQCP DIRECTION MAXIMIZE
SOLVER COUENNE FROM LINE 49
**** SOLVER STATUS 1 Normal Completion
**** MODEL STATUS 1 Optimal
**** OBJECTIVE VALUE 0.0121
---- 50 VARIABLE area.L = 0.012
---- 50 VARIABLE r.L coordinates of rectangle
lo up
x 0.939 0.982
y 0.720 1.000
This is obviously a bad and non-optimal solution. I don't know what is going on here, but this looks like a bug.
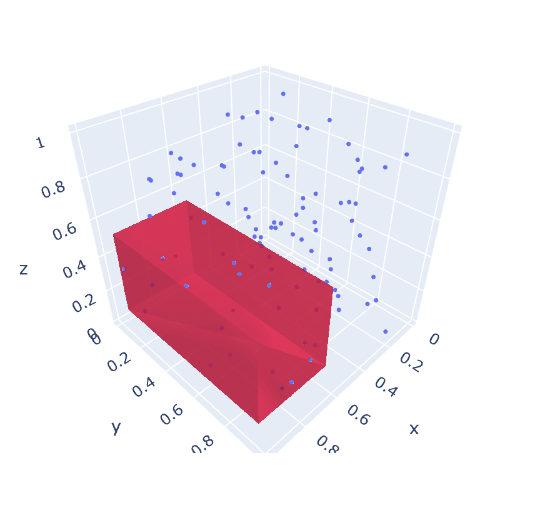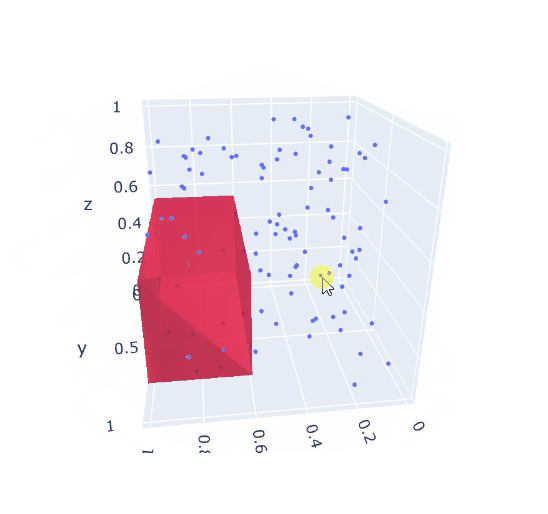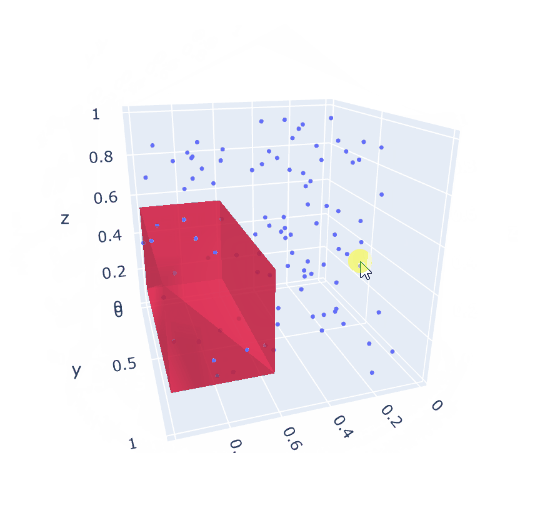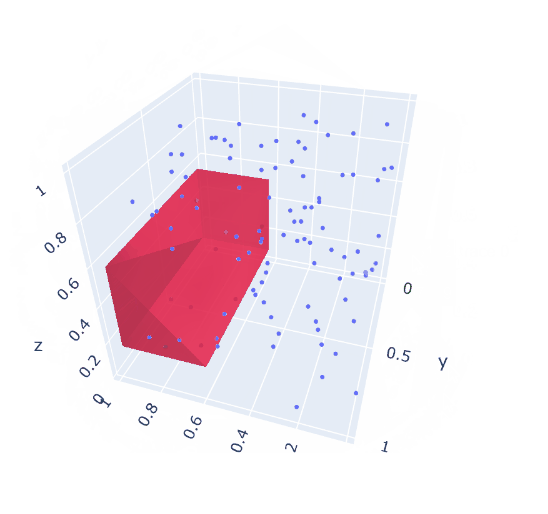
1b. 3d largest box
It is easy to make a 3d version of the model above. Just replace \(c = \{x,y\}\) by \(c = \{x,y,z\}\). Unfortunately, there is one complication: now the model has an objective that is no longer quadratic. However, this can be fixed by chaining: \[\begin{align} \max\>&\mathit{volume} = \mathit{area}\cdot \mathit{side}_{z}\\ & \mathit{area} = \mathit{side}_{x} \cdot \mathit{side}_{y} \\ & \mathit{side}_c = r_{c,up}-r_{c,lo} && \forall c \end{align}\]
A solution can look like:
---- 52 VARIABLE area.L = 0.340 VARIABLE volume.L = 0.146 ---- 52 VARIABLE r.L coordinates of 3D box lo up x 0.608 0.998 y 0.091 0.963 z 0.140 0.571
Note that Cplex can not handle this problem: Cplex allows non-convexities in the objective only (apart for some cases where it can reformulate things).
 |
| 3d version: largest box not clashing with given points |
2. Hostile Brothers Problem
A father is facing the following problem. He has has a plot of land. And he has \(n\) sons, who don't get along at all. In order to minimize friction, he wants to build a house for each of his sons, such that the minimum distance between them is maximized. The mathematical model can look like:
| Hostile Brothers Problem |
|---|
| \[\begin{align} \max\> & \color{darkred}z \\ & \color{darkred}z \le \sum_{c} (\color{darkred}x_{i,c}-\color{darkred}x_{j,c})^2&& \forall i\lt j\\ & \color{darkred}x_{i,c} \in [\color{darkblue}L,\color{darkblue}U]\end{align} \] |
Here \(i\) indicates the point, \(i \in \{1,\dots,n\}\) and \(c\) is the coordinate. For a 2D problem, we have \(c \in \{x,y\}\).
When we use \(n=50\) random points, Gurobi is not able to even come close to proven optimality, I used a time limit of 2 hours, and the final gap is enormous:
1560307 1354785 0.40487 42 1653 0.01935 0.67173 3371% 332 7171s 1562085 1356368 cutoff 283 0.01935 0.67173 3371% 332 7177s 1563023 1356980 cutoff 285 0.01935 0.67173 3371% 332 7180s 1564565 1358071 0.01937 248 930 0.01935 0.67173 3371% 332 7190s 1565720 1359205 0.60071 48 1510 0.01935 0.67173 3371% 332 7196s 1567335 1359826 cutoff 272 0.01935 0.67173 3371% 332 7200s Cutting planes: RLT: 1312 Explored 1567341 nodes (520860935 simplex iterations) in 7200.00 seconds Thread count was 8 (of 16 available processors)
Summary:
- Best found solution: 0.01935
- Best possible objective value: 0.6173
- Relative gap: 3371%
The big gap is partly due to the small best-found solution (0.01935). But mainly: this is a very difficult job for Gurobi. Even when the problem is relatively small: just 100 continuous variables,
By inspecting the solution, we see this solution is not very good at all:
 |
| Solution found by Gurobi after 2 hours (obj=0.01935) |
I expect a much more regular pattern.
We can try to improve performance by noticing there is much symmetry in the model. The same solution can be obtained by just renumbering the points. To break symmetry, I added the constraint: \[\sum_c x_{i,c} \ge \sum_c x_{i-1,c}\] This was not very successful:
2978972 2407171 0.01708 130 813 0.00885 0.64271 7159% 222 7180s 2981109 2409232 0.52720 64 2378 0.00885 0.64271 7159% 222 7185s 2984648 2411500 0.20399 107 2156 0.00885 0.64271 7159% 222 7191s 2986302 2412811 0.12220 127 1721 0.00885 0.64271 7159% 222 7195s 2987852 2413879 0.06942 175 1728 0.00885 0.64271 7159% 222 7200s Explored 2988184 nodes (662244035 simplex iterations) in 7200.01 seconds Thread count was 8 (of 16 available processors)
So we see:
- The best-found solution (0.00885) is worse than before (0.01935)
- The best possible solution (0.64271) is worse than before (0.6173)
- The relative gap is worse (7159% vs 3371%)
As an alternative, let's try Baron on this model. I dropped the symmetry breaking constraint here (adding this constraint was not beneficial, at least not during the initial period of the search). We see in the first few minutes:
Iteration Open nodes Time (s) Lower bound Upper bound * 1 1 5.51 0.257746E-01 2.00000 * 1 1 7.22 0.274782E-01 2.00000 1 1 7.41 0.274782E-01 2.00000 12 7 49.51 0.274782E-01 1.72727 31 16 80.03 0.274782E-01 1.72727 46 24 111.27 0.274782E-01 1.72727
I.e. Baron finds a much better solution very quickly (but is far from getting the gap close to zero).
Another approach is to use a multi-start approach with a local NLP solver. Generate a random starting point, solve, and repeat. When I do this 20, I see when I use the CONOPT NLP solver:
Another approach is to use a multi-start approach with a local NLP solver. Generate a random starting point, solve, and repeat. When I do this 20, I see when I use the CONOPT NLP solver:
---- 57 PARAMETER objs objective values of NLP solver cycle1 0.02751, cycle2 0.02669, cycle3 0.02705, cycle4 0.02041, cycle5 0.02620, cycle6 0.01235 cycle7 0.02675, cycle8 0.02590, cycle9 0.02660, cycle10 0.02679, cycle11 0.02558, cycle12 0.02644 cycle13 0.02622, cycle14 0.02625, cycle15 0.02620, cycle16 0.02749, cycle17 0.02742, cycle18 0.02692 cycle19 0.02675, cycle20 0.02688, best 0.02751
This is the best we have seen so far. By accident, the best results were found in the first cycle. The results look like:
 |
| Best solution with Multi-start Conopt (obj=0.02751) |
This solution looks much better than the one Gurobi found. In addition, CONOPT needs only 30 seconds to solve these 20 problems.
Conclusion:
- Cplex cannot solve this problem
- Gurobi finds a solution with objective 0.01935 (time limit: 2 hours)
- Baron finds a solution of 0.02748 in 100 seconds
- Conopt finds a solution of 0.02751 in a loop of 20 solves that takes 30 seconds
- Increasing this to 200 solves gives an objective of 0.02771
- Remember that we are maximizing
Even though this is a non-convex quadratic problem, it makes sense to look beyond quadratic solvers.
SAS NLP multistart yields 0.027723 in 100 seconds.
ReplyDeleteproc optmodel;
ReplyDeletenum n = 50;
var X {1..n} >= 0 <= 1;
var Y {1..n} >= 0 <= 1;
var Z;
max Objective = Z;
con MaxMin {i in 1..n, j in i+1..n}:
Z <= (X[i] - X[j])^2 + (Y[i] - Y[j])^2;
solve with nlp / ms=(maxtime=100);
create data outdata from [i] X Y;
quit;
For an amusing application of this model to U.S. flag design, see https://blogs.sas.com/content/operations/2017/07/03/fun-with-flags-optimizing-arrangements-of-stars-with-sas/
ReplyDeleteThe sentence "Cplex can not handle this problem" is far too strong since within CPLEX you also have a Constraint Programming engine CPOptimizer that works quite well on those 3 problems.
ReplyDeleteLargest empty rectangle : Gives optimal solution in less than 1 s
Largest empty box : Gives 0.18 in 2 s
Hostile brothers : Gives 0.0244 with a 60 s time limit
I posted the 3 OPL models in https://www.linkedin.com/pulse/tips-tricks-opl-cplex-alex-fleischer/
Is there any benefit to limiting the comparison of z? If you add the symmetry constraints AND also reduce the number of constraints for which z is constrained, will that help? For example, we know that the constraint given for z between points 1 and 50 (lower left and upper right) is not going to constrain the value of z. In the above problem there are a limited number of points that are closest. Is there a way to determine a-priori which of the points are supposed to be closest to point i?
ReplyDelete