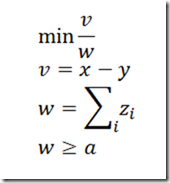In a fairly complex model, we ended up trying a nonlinear objective:

where the rest of the model was linear (after applying some reformulations). As the model contains both integer and binary variables, this now has become an MINLP.
For several reasons this is actually not a very good expression:
- this expression generates a lot of non-linear variables and non-linear non-zero elements in the matrix
- as some z(i)’s can be zero it is difficult to protect this against division-by-zero (although the way we ran it had a linear model in front of this model, so our starting point was reasonable and no division-by-zero occurred)
A better formulation would be:
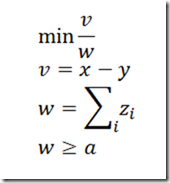
Here we only have two non-linear variables: the rest of the variables is now appearing linearly in the constraints. In addition, although we cannot bound each z(i) away from zero, we could introduce a nonzero lower bound on w.
Although we are adding extra constraints and variables to the MINLP model, this actually makes the model easier to solve and more robust.
PS1. The model is now becoming somewhat complex as we try to deal with different types of decisions in the same model. We call this an “integrated model” rather than just messy!
PS2. In some cases fractions can be reformulated using a “fractional programming” technique. In practice for larger models this often turns out to be a difficult reformulation to implement.
Question: it is suggested in a comment below to use (2d?) bisection. Is that really a good idea? Any references for such an approach applied in a similar situation?