| $ontext
Olafur P. Pallson, Hans F. Ravn
Scenario Analysis and the Progressive Hedging Algorithm
- Simple Numerical Examples
The Technical University of Denmark, 1993
$offtext
set
iter 'iteration number' /it0*it20/
n 'nodes' /I,II,III,IV, s1*s6/
s(n) 'scenarios: leaf nodes' /s1*s6/
t 'levels: dimension of x' /t1*t3/
dp(n) 'decision points in tree' /I,II,III,IV/
tt(t) "subset of t's used in current scenario"
;
alias(n,nn,nnn);
table tree(n,nn,*)
value prob
I.II 5 0.3
II.s1 6 0.2
II.s2 5 0.5
II.s3 2 0.3
I.III 2 0.7
III.s4 4 0.6
III.IV 7 0.4
IV.s5 6 0.1
IV.s6 4 0.9
;
display tree;
*
* do some tree manipulations here
*
set paths(s,n,nn) 'links on path to leaf node';
paths(s,n,s)$tree(n,s,'prob')=yes;
scalar cnt;
* repeat augment paths until no more change
repeat
cnt = card(paths);
paths(s,nnn,n)$(sum(nn,paths(s,n,nn)) and tree(nnn,n,'prob')) = yes;
until cnt=card(paths);
option paths:0:0:1;
display paths;
set top(n) 'top of tree';
top(n)$(sum((s,nn)$paths(s,nn,n),1)=0) = yes;
display top;
parameter level(n) 'level of each node in tree';
level(top)=1;
repeat
cnt = card(level);
loop(paths(s,n,nn)$level(n),
level(nn) = level(n)+1;
);
until cnt=card(level);
display level;
alias(t,tdown,tup);
parameters
sprob0(s,t) 'single probabilities'
sprob1(s,t) 'accumulated probabilities'
sval(s,t) 'values'
;
sval(s,t) = sum(paths(s,n,nn)$(level(n)=ord(t)), tree(n,nn,'value'));
display sval;
sprob0(s,t) = sum(paths(s,n,nn)$(level(n)=ord(t)), tree(n,nn,'prob'));
display sprob0;
* accumulate probabilities backwards to get conditional probabilities
sprob1(s,t)$sprob0(s,t) = prod(tdown$(ord(tdown)>=ord(t) and sprob0(s,tdown)), sprob0(s,tdown));
display "table 4a",sprob1;
set stdp(s,t,dp) 'mapping to decision points';
stdp(s,t,dp)$sum(paths(s,dp,nn)$(level(dp)=ord(t)), 1) = yes;
option stdp:0:1:2;
display stdp;
set tdp(t,dp) 'extracted from stdp for a given scenario';
parameter
Xs(s,t)
Ws(s,t) 'price'
W(t)
d(t)
xhat(dp) 'conditional expectation'
report(iter,*,*) 'table 1: results from iterations'
x0(t) /t1 4/
;
Ws(s,t) = 0;
w(t) = 0;
xhat(dp) = 0;
scalars
iterno
continue /1/
r 'penalty parameter'/0/
;
variables
x(t) 'for submodel'
z 'for submodel'
;
equations
obj
;
obj.. z =e= sum(tt(t),0.5*sqr(x(t)-x(t-1)-x0(t))+sqr(x(t)-d(t)))
+ sum(tt(t),w(t)*x(t)) + 0.5*r*sum(tt(t),sqr(x(t)-sum(tdp(t,dp),xhat(dp))));
x.lo(t)=3;
x.up(t)=6;
model m /obj/;
* reduce output and increase speed in loop
m.solprint = 2;
m.solvelink = %Solvelink.LoadLibrary%;
option xhat:2;
display xhat;
set report_iter(iter) /it0*it5,it10,it15,it20/;
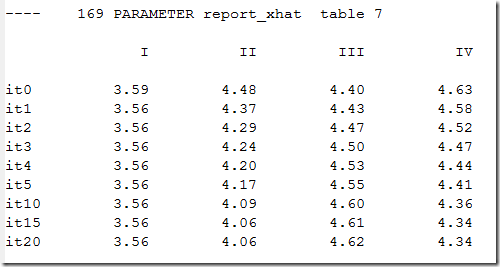
parameter report_xhat(iter,dp) 'table 7';
loop(iter$continue,
iterno = ord(iter);
display '***** iteration ******',iterno;
* r = 0 in first iteration (it0)
r = 1$(iterno>1);
* step 1
* solve each scenario
Xs(s,t)=0;
loop(s,
d(t) = sval(s,t);
tdp(t,dp) = stdp(s,t,dp);
tt(t) = sum(tdp(t,dp),1);
w(t) = ws(s,t);
solve m minimizing z using nlp;
Xs(s,tt(t)) = x.l(t);
);
display Xs;
* step 2
* Calculate policy Xhat
xhat(dp) = sum(stdp(s,t,dp), Xs(s,t)*sprob1(s,t));
display Xhat;
* step 3
* Update W
Ws(s,t) = Ws(s,t) + r*(xs(s,t) - sum(stdp(s,t,dp),xhat(dp)));
display Ws;
report_xhat(iter,dp)$report_iter(iter) = xhat(dp);
);
display report_xhat; |