Unit Loss Function

A standard normal unit loss function can be described as:

  

where f(x) is the standard normal density function and F(x) is the standard normal CDF. See: http://planetmath.org/unitnormallossfunction.

Often we want to solve UNL(x)=c for x.

GAMS Version

$ontext    Standard Normal Unit Loss Function (UNL)    solve UNL(x)=c    for a given c    Method: solve f(x) - x * (1-F(x)) = c    where f is standard normal density function and F is the standard    normal CDF. $offtext scalar c /0.0331/; variable x; equation e; e..  1/sqrt(2*pi)*exp(-0.5*sqr(x)) - x * (1-errorf(x)) =e= c; * initial value x.l = 1; model m /e/; solve m using cns; display x.l;

This solves with CONOPT very quickly, we get:

Note: the GAMS math expressions can be inspected with a new tool. This is a nice test example:

Wolfram Alpha

The input is easy:

The output is unfortunately:

Mathematica

The above approach is not really suited for Mathematica. This looks better:

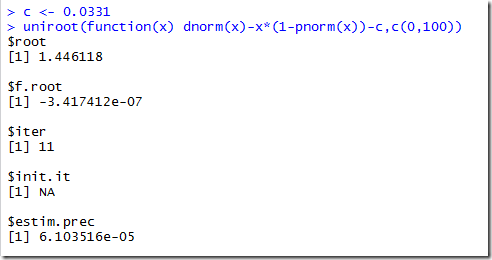
R

Super easy input, due to predefined functions for normal pdf and cdf. We give an interval of [0,100] to search:

Excel

Its root finder is called Goal Seek.

It is a little bit sloppy by default. We can make Goal Seek more precise by multiplying the UNC-c cell by a 1000:

  

Note: the tolerance can also be set in the Excel options (under formulas, Maximum Change). Looks like Excel is using an absolute tolerance on Δx and Δf (i.e. it could stop prematurely if the algorithm chooses a very small Δx).

Python

Quite nice: