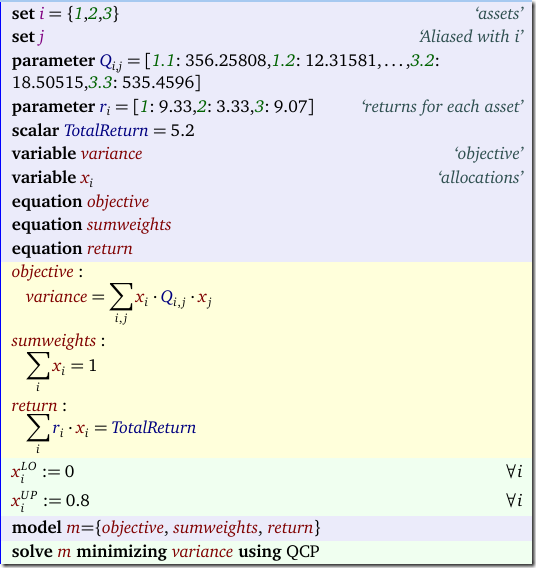
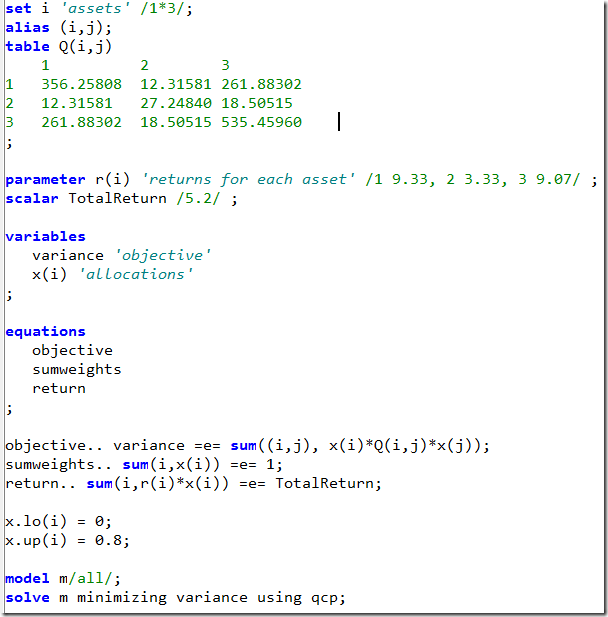
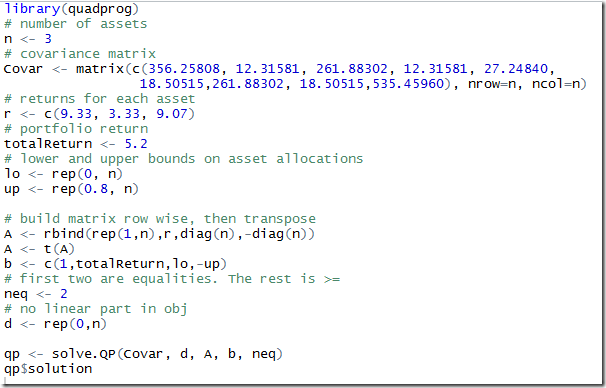
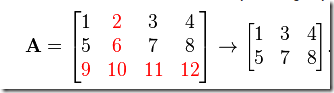
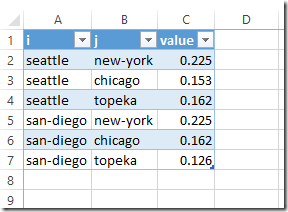
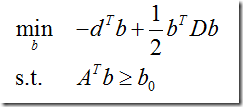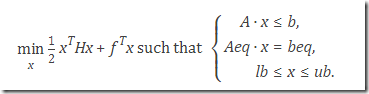Given a set of numbers with mean μ0 find a subset of at most K numbers that has a mean μ that is as close as possible to μ0.Of course we try immediately to cast this as an optimization problem. The obvious MINLP formulation would be:

There are a number of interesting aspects. Not all of them are completely trivial.
We added a lowerbound of 1 to cnt (the size of the subset). This way we can safely divide by cnt. We could replace the division by a multiplication (this is the usual approach to protect against 'division by zero'), but in this case this is not needed anymore. Also note that a mean or average of zero numbers is not really defined, so this lowerbound really makes sense.
This model contains two non-linearities: (1) the objective is quadratic and (2) we have this division in constraint avg. Note that if we would only consider subsets of exactly size K our problem becomes much simpler. In that case cnt would not be a variable but rather a constant parameter and the avg constraint would become automatically linear.
An obvious but interesting question is whether we can linearize this model. The quadratic objective can be approximated by using an absolute value measure. Actually there is some monotic transformation between the quadratic and absolute value criterion. This mans we will reach the same optimal solution using the absolution value method as using the quadratic objective.
The division is more complicated. However we can note that we can rewrite equations count and avg as follows:
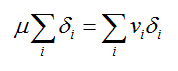
This can be linearized as follows:

As usual it is important to find good, tight values for the big-M's. In this case we can find reasonably good values:

where μLO and μUP are bounds on μ, e.g. μLO=min{vi}, μUP=max{vi}.
Now lets put everything together:


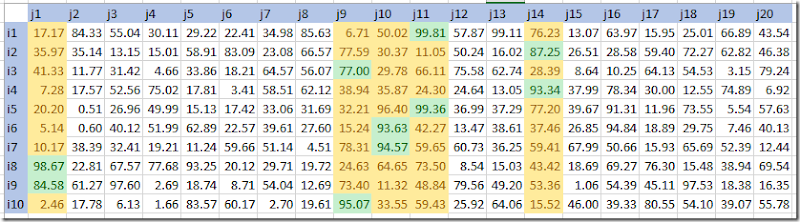
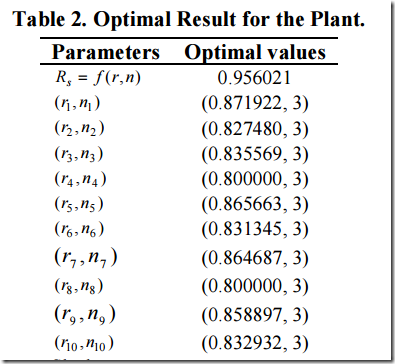
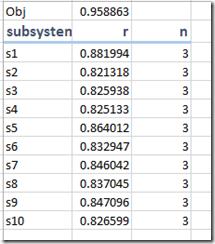
Here are some results:

We see that for K=5 we actually just use 4 numbers.









![image_thumb[1] image_thumb[1]](https://lh3.googleusercontent.com/--TCUXltruyo/VnwVToRL4iI/AAAAAAAAEjs/EEQ8b0KWLsE/image_thumb%25255B1%25255D_thumb%25255B1%25255D.png?imgmax=800)
![image_thumb[3] image_thumb[3]](https://lh3.googleusercontent.com/-n8OOgjOgO1s/VnwVUlJnWpI/AAAAAAAAEj8/u8aoIMDFBhs/image_thumb%25255B3%25255D_thumb%25255B1%25255D.png?imgmax=800)
![image_thumb[5] image_thumb[5]](https://lh3.googleusercontent.com/-ZY2_LvIJmgc/VnwVWekY1DI/AAAAAAAAEkg/er20bLcerjk/image_thumb%25255B5%25255D_thumb%25255B1%25255D.png?imgmax=800)