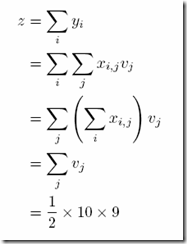In http://www-cs-faculty.stanford.edu/~knuth/fasc2b.ps.gz we find the huge alphametic (I like the term cryptarithm mentioned as alternative even better):
| | | | | | | | | | A | N |
| A | C | C | E | L | E | R | A | T | I | N | G |
| I | N | F | E | R | E | N | T | I | A | L |
| E | N | G | I | N | E | E | R | I | N | G |
| | | | | | | | T | A | L | E |
| | | | | | | E | L | I | T | E |
| | | | | | | G | R | A | N | T |
| | | | | | | | | F | E | E |
| | | | | | | | | | E | T |
| | | | | | C | E | T | E | R | A |
|
| | A | R | T | I | F | I | C | I | A | L |
| I | N | T | E | L | L | I | G | E | N | C | E |
The simple formulation from this posting leads to problems even for Cplex. The stable formulation from this posting is a winner here: it yields a quick solution that is correct.
Simple formulation
$ontext
Alphametics, Simple formulation
This does not work very well.
Erwin Kalvelagen
AN
+ ACCELERATING
+ INFERENTIAL
+ ENGINEERING
+ TALE
+ ELITE
+ GRANT
+ FEE
+ ET
+ CETERA =
-------------
ARTIFICIAL
+ INTELLIGENCE
$offtext
set i /A,N,C,E,L,R,T,I,G,F/;
alias (i,j);
set leading(i) /A,I,E,T,G,F,C/;
abort$(card(i) <> 10) "set i should have 10 elements";
parameter v(i); v(i) = ord(i)-1;
variables
y(i) 'decision variables'
x(i,j) 'auxiliary variables for uniqueness'
z 'dummy objective variable'
;
binary variable x;
equation
addition 'the actual problem'
ydef(i) 'calculate y'
xrow(i) 'row sums'
xcol(j) 'column sums'
dummy_objective
;
addition..
10*y('A')+y('N')+
1e11*y('A')+1e10*y('C')+1e9*y('C')+1e8*y('E')+1e7*y('L')+1e6*y('E')+1e5*y('R')+1e4*y('A')+1e3*y('T')+100*y('I')+10*y('N')+y('G')+
1e10*y('I')+1e9*y('N')+1e8*y('F')+1e7*y('E')+1e6*y('R')+1e5*y('E')+1e4*y('N')+1e3*y('T')+100*y('I')+10*y('A')+y('L')+
1e10*y('E')+1e9*y('N')+1e8*y('G')+1e7*y('I')+1e6*y('N')+1e5*y('E')+1e4*y('E')+1e3*y('R')+100*y('I')+10*y('N')+y('G')+
1e3*y('T')+100*y('A')+10*y('L')+y('E')+
1e4*y('E')+1e3*y('L')+100*y('I')+10*y('T')+y('E')+
1e4*y('G')+1e3*y('R')+100*y('A')+10*y('N')+y('T')+
100*y('F')+10*y('E')+y('E')+
10*y('E')+y('T')+
1e5*y('C')+1e4*y('E')+1e3*y('T')+100*y('E')+10*y('R')+y('A') =e=
1e9*y('A')+1e8*y('R')+1e7*y('T')+1e6*y('I')+1e5*y('F')+1e4*y('I')+1e3*y('C')+100*y('I')+10*y('A')+y('L')+
1e11*y('I')+1e10*y('N')+1e9*y('T')+1e8*y('E')+1e7*y('L')+1e6*y('L')+1e5*y('I')+1e4*y('G')+1e3*y('E')+100*y('N')+10*y('C')+y('E');
ydef(i).. y(i) =e= sum(j, x(i,j)*v(j));
xrow(i).. sum(j, x(i,j)) =e= 1;
xcol(j).. sum(i, x(i,j)) =e= 1;
*
* bounds on leading digits: they can not be 0
*
y.lo(leading) = 1;
dummy_objective.. z =e= sum(i, y(i));
model m /all/;
m.optfile=1;
solve m using mip minimizing z;
option y:0;
display y.l;
The numbers in the addition equation are really become too big for comfort. It is surprising that some solvers such as Gurobi can deliver a good solution for this model, but as expected some others can not. The poor scaling can create severe havoc. The model can be downloaded from here.
Stable formulation
$ontext
Alphametics, stable formulation
AN
+ ACCELERATING
+ INFERENTIAL
+ ENGINEERING
+ TALE
+ ELITE
+ GRANT
+ FEE
+ ET
+ CETERA =
-------------
ARTIFICIAL
+ INTELLIGENCE
Erwin Kalvelagen, 2009
$offtext
set
i 'letters' /A,N,C,E,L,R,T,I,G,F/
w 'words' /an,accelerating,inferential,engineering,tale,elite,grant,fee,et,cetera,
artificial,intelligence/
w1(w) /an,accelerating,inferential,engineering,tale,elite,grant,fee,et,cetera/
w2(w) /artificial,intelligence/
;
alias (i,j);
abort$(card(i) <> 10) "set i should have 10 elements";
set
k 'slices (slice1 if rightmost slice)' /slice1*slice12/
lead(i) 'leading letters' /A,I,E,T,G,F,C/
;
set letters(w,i,k) /
an.(a.slice2, n.slice1)
accelerating.(a.slice12, c.slice11, c.slice10, e.slice9, l.slice8, e.slice7,
r.slice6, a.slice5, t.slice4, i.slice3, n.slice2, g.slice1)
inferential.(i.slice11, n.slice10, f.slice9, e.slice8, r.slice7, e.slice6,
n.slice5, t.slice4, i.slice3, a.slice2, l.slice1)
engineering.(e.slice11, n.slice10, g.slice9, i.slice8, n.slice7, e.slice6,
e.slice5, r.slice4, i.slice3, n.slice2, g.slice1)
tale.(t.slice4, a.slice3, l.slice2, e.slice1)
elite.(e.slice5, l.slice4, i.slice3, t.slice2, e.slice1)
grant.(g.slice5, r.slice4, a.slice3, n.slice2, t.slice1)
fee.(f.slice3, e.slice2, e.slice1)
et.(e.slice2, t.slice1)
cetera.(c.slice6, e.slice5, t.slice4, e.slice3, r.slice2, a.slice1)
artificial.(a.slice10, r.slice9, t.slice8, i.slice7,
f.slice6, i.slice5, c.slice4, i.slice3, a.slice2, l.slice1)
intelligence.(i.slice12, n.slice11, t.slice10, e.slice9, l.slice8, l.slice7,
i.slice6, g.slice5, e.slice4, n.slice3, c.slice2, e.slice1)
/;
parameter lhs(k,i), rhs(k,i);
lhs(k,i) = sum(letters(w1,i,k),1);
rhs(k,i) = sum(letters(w2,i,k),1);
parameter v(i); v(i) = ord(i)-1;
variables
y(i) 'decision variables'
x(i,j) 'auxiliary variables for uniqueness'
carry(k)
z 'dummy objective variable'
;
binary variable x;
integer variable carry;
equation
addition(k) 'the actual problem'
ydef(i) 'calculate y'
xrow(i) 'row sums'
xcol(j) 'column sums'
dummy_objective
;
addition(k)..
carry(k-1) + sum(i, lhs(k,i)*y(i)) =e=
sum(i, rhs(k,i)*y(i)) + 10*carry(k);
carry.fx('slice12')=0;
ydef(i).. y(i) =e= sum(j, x(i,j)*v(j));
xrow(i).. sum(j, x(i,j)) =e= 1;
xcol(j).. sum(i, x(i,j)) =e= 1;
*
* bounds on leading digits: they can not be 0
*
y.lo(lead) = 1;
dummy_objective.. z =e= sum(i, y(i));
model m /all/;
solve m using mip minimizing z;
option y:0;
display y.l;
The solution I get is:
---- 106 VARIABLE y.L decision variables
A 5, N 9, C 7, E 4, R 2, T 1, I 6, G 8, F 3 |
where y(‘L’)=0 is implied. This formulation is stable: it yields correct solutions for all MIP solvers. The model can be downloaded here.