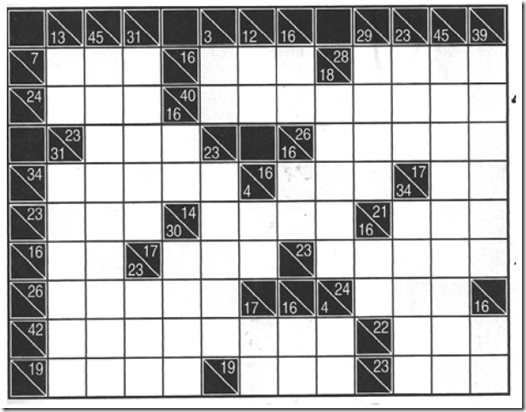
I see a lot of GAMS models. Some of them are really beautifully done. Others, I would like to suggest some edits. Here we compare two different models that solve a Kakuro puzzle. The problem from (1) is here:
We need to fill in the white cells with numbers \(1,…,9\). Each horizontal or vertical region of consecutive white cells has to add up to the number in the black cell just above to to the left. Furthermore each number in each region has to be unique. The solution of the above puzzle is (again from (1)):
We have the following two models:
- MODEL A: taken from (1). The appendix has a GAMS model.
- MODEL B: developed independently by me, discussed in (2)
In the following I try to show things next to each other: MODEL A (1) at the left and MODEL B (2) to the right.
The differences between the models vary between mundane syntax or style issues, and more substantial differences in the underlying optimization model. In some cases I do things differently because of taste and customs, in others I may have a good reason to write things down differently.
| MODEL A | MODEL B |
 | sets |
Instead of using numbers as set elements, I prefer to prefix them by a distinguishing (short) name. This is especially useful when displaying and viewing high-dimensional data. Of course we add some explanatory text. I prefer to put them in quotes to create a visual barrier between the set name and the explanatory text and because things like a comma can unexpectedly end an explanatory text without quotes. Many GAMS models create spurious sets, parameters etc. because there is a comma in the explanatory text.
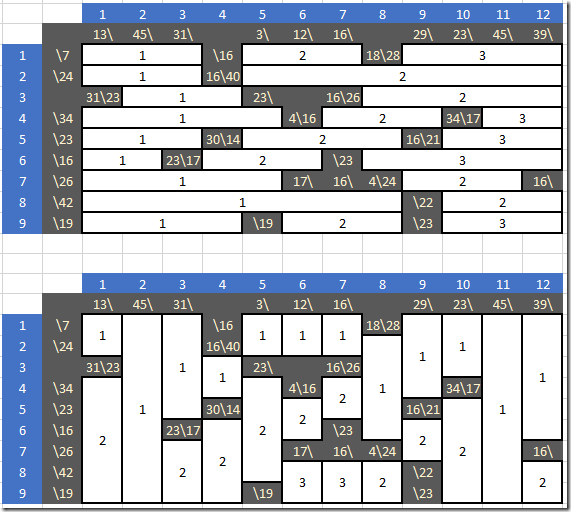
The blocks or segments have a different numbering scheme. In model A we number them as follows:
The maximum number of segments in a row or column is three, which explains the set seg in model A.
In model B the numbering scheme is global:
Here we have 47 different blocks. Somehow model A calls regions “segments” and in model B they are called “blocks”.
| MODEL A | MODEL B |
I tend to keep variables together and put them after data entry and data manipulation. You will see the variable declarations in model B further down.
 |
The data structures in model A indicate the number of segments in each row (and column), their starting and end-position and the required summation value. This gives rise to eight different parameters.
The left model A has a lot of individual assignment statements. That is not the most compact way to initialize data. GAMS has parameter initialization syntax for this. E.g. we could have written the initialization of n_segs_l as:
parameter n_segs_l(i) /
(2,3,7,8) 2
(1,4,5,6,9) 3
/;
The right model B has just one parameter block that has all the needed information. This approach has just one mapping between block number \(k\) and a bunch of cells with coordinates \((i,j)\) and also has the summation value. In the derived data we extract data in a form that is easier to use in the rest of the model.
 |
This looks like a somewhat unusual approach. I will discuss this further down at the spot where these equations are defined.
| MODEL A | MODEL B |
| binary variable x(i,j,k) 'assignment'; |
Remember that Model A had binary variable a_bin(i,j,v) declared earlier. Model B has an extra variable \(v\) which will help us keeping the equations simpler and also to reduce the number of non-zero elements in the LP matrix \(A\).
The naming of identifiers (names of sets, parameters, variables and equations) is somewhat a matter of taste. Admittedly, \(x\) is not the most self-descriptive name, but I like it if there is a single central variable that really plays a dominating role the model. Often I like to use a naming scheme where I use very short names for identifiers that are used a lot, and longer, more descriptive names for identifiers less often used in the model. That would imply, my equation names are longer:
| equation declarations are not listed | equations |
The equations are defined below:
 | oneval(ij(i,j)).. |
Model A is putting this constraint on each black and white cell. Hence it is a \(\le\) constraint. This is somewhat of a disadvantage as the solution is no longer unique, and we need an objective to help us preventing zero values in the white cells. A better formulation is in model B where we run only over the white cells and thus can use a \(=\) constraint. This will yield a stronger MIP formulation.
 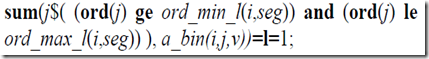 | unique(b,k).. |
Model A has a complex equation, because it tries to find all line segments in a row \(i\). In Model B we have a much simpler equation that is actually more powerful: it handles both the row and column blocks in one swoop. I like to make the equations as simple as possible as equations are more difficult to debug. The set sblock helps us to simplify this constraint. By definition sblock only refers to white cells.
| MODEL A | MODEL B |
 | defval(ij(i,j)).. v(i,j) =e= sum(k, ord(k)*x(i,j,k)); sumblock(b).. sum(sblock(b,i,j), v(i,j)) =e= bval(b); |
On the left we have again a very complicated equation for the row segments. On the right we split the logic in two parts: the first equation calculates the integer value \(v_{i,j}\) of a cell \((i,j)\). The second equation sums up the values in a block \(b\) and make sure this sum has the correct value. This equation handles both row-wise blocks and column-wise blocks. Note again that we only operate on the white cells.
Each white cell \((i,j)\) is part of two blocks (row and column). By introducing an intermediate variable \(v_{i,j}\) I prevent duplication of the expression \(\sum_k k\cdot x_{i,j,k}\). This formulation makes the model larger but sparser.
 |
Here the model A introduces a lot of equations to force the “black” cells to zero.
First, this is not my preferred way to do this. We can make a subset black(i,j) (containing the coordinates of all black cells) and then just say:
undefined_value(black(i,j),v).. a_bin(i,j,v) =e= 0;
Of course we can do this more compactly by setting bounds instead of using a full-blown equation:
a_bin.fx(black(i,j),v) = 0;
Even better is just not generate any variable with \((i,j)\) outside the white cells. In model B we have created a convenient set for that: \(IJ(i,j)\): this subset has only the “white” cells. I make sure all equations only operate on the white cells and never touch the black cells. This requires a little bit more thought and discipline but I prefer this approach.
 |
In model B we handled these constraints already as we dealt with row and column-wise blocks in one single constraint.
| MODEL A | MODEL B |
 | edummy..
model m /all/; |
On the left we have a real objective to prevent zeroes in the white cells. Probably we should add
option optcr=0;
to force the MIP solver to find the global optimum with a gap of zero. Note that MODEL B does not need any optcr as we only look for a feasible integer solution.
The display of a_bin.l is not very convenient to view. It looks like:
A better display can be achieved by:
parameter w(i,j);
w(i,j) = sum(v,ord(v)*a_bin.l(i,j,v));
option w:0;
display w;
That would lead to a similar output as produced by model on the right:
| ---- 119 VARIABLE v.L cell values c1 c2 c3 c4 c5 c6 c7 c8 c9 r1 4 2 1 1 8 7 8 + c10 c11 c12 r1 9 4 7 |
The final question is: how do these models perform? I ran the problem with the open source solver CBC (1 thread):
| MODEL A | MODEL B |
| Search completed - best objective -88, took 32349 iterations and 854 nodes (14.82 seconds) | Search completed - best objective 0, took 215 iterations and 0 nodes (0.68 seconds) |
As expected a MIP solver prefers the tighter formulation of MODEL B.
Notes
- Model B is much more compact. We can quantify this as follows: Model A has about 432 lines, Model B 119 lines. This includes data entry.
- Model A uses the ord(.) function 12 times, Model B only uses the ord(.) function once. Often models with lots of ord()’s are more likely to be messy models.
References
- José Barahona da Fonseca, A novel linear MILP model to solve Kakuro puzzles, 2012. http://www.apca.pt/publicacoes/6/paper56.pdf (This is referred to as MODEL A)
- MODEL B is: http://yetanothermathprogrammingconsultant.blogspot.com/2017/02/solving-kakuro-puzzles-as-mip.html