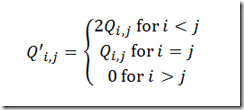Symmetry

From http://groups.google.com/group/ampl/browse_thread/thread/7c849e1de871b22b:

Dear all, I would like to know how to model the property of symmetry in AMPL. For example, how can I tell AMPL that  x [1,3] and x [3,1] is the same thing in my model and script? Best Regards

If x is a variable, something like the following: set N; # index set var x{N,N}; s.t. Symmetry {i in N, j in N : i <> j}: x[i,j] = x[j,i]; Paul

I would like to add that anytime I see something like this, there is a possibility to exploit such a feature.

If x[i,j] is symmetric we can reduce the size of x by only considering the (lower or upper) triangular part of x. This is the case both when x is a variable or when x is a parameter. An example for exploiting this in a variable is documented here: http://yetanothermathprogrammingconsultant.blogspot.com/2012/02/weddings-and-optimal-seating.html. The set gt(g1,g2) is used many times here to reduce the size of variable meet(g1,g2).

A well known example of symmetric data is the portfolio optimization problem. If the variance-covariance matrix is large and dense it certainly helps to consider only half of it. Here is a way to exploit a symmetric Q matrix which can be used in many QP models with x’Qx in the objective:

Even if Q is not symmetric we can make it symmetric by something like q(i,j) =  0.5(q(i,j)+q(j,i)).

Of course one could argue that MIP solvers and their presolvers are getting smarter and we don’t need this anymore. This is indeed sometimes the case for the better solvers. However, for larger instances we should not only consider the solver but also time spent in generating the model. Often these tricks can make a significant impact on overall performance and total turnaround time of jobs.

Some computational evidence is here regarding a large portfolio QP model (synthetic dataset with 2K instruments):

As you can see Cplex does not really care whether QP is full or triangular (the small difference in time is related to reading the Q data: there is more data when Q is full). However GAMS is twice as fast when we use a triangular Q. Aside from this it is noted that GAMS is not very fast compared to Cplex on these models. The processing of the nonlinear terms is relatively expensive.

For completeness I want to mention that for this portfolio optimization problem there is an alternative formulation using the mean adjusted returns directly. This formulation leads to a QP with a diagonal Q matrix. The timings for the same data set are:

GAMS benefits greatly from this easier formulation, but also Cplex is faster.

Interesting Methodology Paper

 

http://papers.ssrn.com/sol3/papers.cfm?abstract_id=1850704

False-Positive Psychology: Undisclosed Flexibility in Data Collection and Analysis Allows Presenting Anything as Significant

• Joseph P. Simmons: University of Pennsylvania - Operations & Information Management Department
• Leif D. Nelson: University of California, Berkeley - Haas School of Business
• Uri Simonsohn: University of Pennsylvania - The Wharton School

Psychological Science, 2011

Abstract:
In this article, we accomplish two things. First, we show that despite empirical psychologists’ nominal endorsement of a low rate of false-positive findings (≤ .05), flexibility in data collection, analysis, and reporting dramatically increases actual false-positive rates. In many cases, a researcher is more likely to falsely find evidence that an effect exists than to correctly find evidence that it does not. We present computer simulations and a pair of actual experiments that demonstrate how unacceptably easy it is to accumulate (and report) statistically significant evidence for a false hypothesis. Second, we suggest a simple, low-cost, and straightforwardly effective disclosure-based solution to this problem. The solution involves six concrete requirements for authors and four guidelines for reviewers, all of which impose a minimal burden on the publication process.

max tricks

The following condition

can be easily written as

 

However when we have:

 

then we need more sophistication. Something like:

Here we introduced a variable y that assumes the value of the maximum of the x’s. The following expression will give a good big-M value:

See also: http://orinanobworld.blogspot.com/2012/01/maxmin-bounds.html

A slightly more direct formulation would be:

If we are really want to show off, we can only generate this if

and use the simpler adjustment of bounds

otherwise.

How to import big GAMS result data into SQL Server

Recently I was involved a few models where GAMS was generating a lot of results, exceeding what we could easily store in Excel or Access. Here is an alternative: store the results in SQL server.

Here is a small two-liner example script that shows how we can efficiently import a very large parameter with 8 million records residing in a GDX file into a SQL server table.

$call gdx2txt.exe in=x.gdx id=p out=p2.txt tab $call bcp testdb.dbo.result in p2.txt -c -S .\SQLEXPRESS –T -h "ROWS_PER_BATCH=8000000,TABLOCK"

The first line exports the parameter from a GDX file to a tab delimited text file. The tool gdx2txt is a little bit more convenient than using GAMS PUT statements and it is also faster (using the same precision more than 5 times as fast).

The second line calls the BCP utility to import this text file.  The hints setting the batch size and requesting a table lock increase the performance.

The log looks like:

--- Job gdx2txt3.gms Start 02/24/12 23:09:02 WEX-WEI 23.7.3 x86_64/MS Windows     GAMS Rev 237  Copyright (C) 1987-2011 GAMS Development. All rights reserved Licensee: Erwin Kalvelagen                               G100803/0001CV-WIN           Amsterdam Optimization Modeling Group                      DC4572 --- Starting compilation --- gdx2txt3.gms(1) 2 Mb --- call gdx2txt.exe in=x.gdx id=p out=p2.txt tab GDX2TXT:Opening "x.gdx" GDX2TXT:Symbol:p Uels:200 GDX2TXT: 100000 records (elapsed 172 millisec) GDX2TXT: 200000 records (elapsed 320 millisec) … GDX2TXT: 7800000 records (elapsed 11201 millisec) GDX2TXT: 7900000 records (elapsed 11343 millisec) GDX2TXT: total records: 8000000 (elapsed 11484 millisec) --- gdx2txt3.gms(2) 2 Mb --- call bcp testdb.dbo.result in p2.txt -c -S .\SQLEXPRESS -T -h "ROWS_PER_BATCH=8000000,TABLOCK" Starting copy... 1000 rows sent to SQL Server. Total sent: 1000 1000 rows sent to SQL Server. Total sent: 2000 1000 rows sent to SQL Server. Total sent: 3000 … 1000 rows sent to SQL Server. Total sent: 7998000 1000 rows sent to SQL Server. Total sent: 7999000 1000 rows sent to SQL Server. Total sent: 8000000 8000000 rows copied. Network packet size (bytes): 4096 Clock Time (ms.) Total     : 24055  Average : (332571.19 rows per sec.) --- Starting execution - empty program *** Status: Normal completion --- Job gdx2txt3.gms Stop 02/24/12 23:09:38 elapsed 0:00:35.736

The total turn around time for this test data was 35 seconds. About 11 seconds for GDX2TXT and 24 seconds for BCP. So the database import is only 2.5 times as slow compared to my time to generate the CSV file. That is very fast indeed. The table had four columns: three GAMS indices (converted to type NCHAR(4)) and a value (type REAL). No (SQL) indices or keys were used against the table so the inserts could be done at optimal speed. Also the db file sizes were extended so they did not need to grow during the inserts. As a result,  in practice the BCP timings may be a bit slower than shown here.

Note: dropping all rows by “DELETE FROM testdb.dbo.result” can take a long time (1.5 minutes on my machine). Much faster is “TRUNCATE TABLE testdb.dbo.result”.

Usage:

C:\projects\gdx2txt>gdx2txt Usage:   gdx2txt in=gdxfile [id=name] [out=txtfile] [csv|tab] Write identifier from GDX file to an ascii file Parameters:    in=gdxfile  name of GDX file, required    id=name     name of identifier, optional if gdx has only one id    out=txtfile name of outputfile, optional, stdout is used otherwise    csv         write ascii file in CSV format    tab         write ascii file in tab delimited format Example:   > gamslib trnsport   > gams trnsport gdx=trnsport   > gdx2txt in=trnsport.gdx id=x   > gdx2txt in=trnsport.gdx id=x out=x.csv csv C:\projects\gdx2txt>bcp usage: bcp {dbtable | query} {in | out | queryout | format} datafile   [-m maxerrors]            [-f formatfile]          [-e errfile]   [-F firstrow]             [-L lastrow]             [-b batchsize]   [-n native type]          [-c character type]      [-w wide character type]   [-N keep non-text native] [-V file format version] [-q quoted identifier]   [-C code page specifier]  [-t field terminator]    [-r row terminator]   [-i inputfile]            [-o outfile]             [-a packetsize]   [-S server name]          [-U username]            [-P password]   [-T trusted connection]   [-v version]             [-R regional enable]   [-k keep null values]     [-E keep identity values]   [-h "load hints"]         [-x generate xml format file]   [-d database name] C:\projects\gdx2txt>

Weddings and optimal seating

In http://www.improbable.com/2012/02/12/finding-an-optimal-seating-chart-for-a-wedding/ an interesting model is proposed about optimal seating arrangements for a wedding. Basically their model looks like (I hope I transcribed the mathematical model correctly):

$ontext   Table assignment   This is the original formulation used in   Meghan L. Bellows   and J. D. Luc Peterson      Finding an optimal seating chart      http://www.improbable.com/2012/02/12/finding-an-optimal-seating-chart-for-a-wedding/   See also:   http://www.hakank.org/constraint_programming_blog/     2011/03/a_matching_problem_a_related_seating_problem_and_some_other_seating_pr.html $offtext set   i 'tables' /table1*table5/   j 'guests' /g1*g17/ ; alias (j,k); table c(j,k)     g1 g2 g3 g4 g5 g6 g7 g8 g9 g10 g11 g12 g13 g14 g15 g16 g17 g1   1 50  1  1  1  1  1  1  1 g2  50  1  1  1  1  1  1  1  1 g3   1  1  1 50  1  1  1  1 10 g4   1  1 50  1  1  1  1  1  1 g5   1  1  1  1  1 50  1  1  1 g6   1  1  1  1 50  1  1  1  1 g7   1  1  1  1  1  1  1 50  1 g8   1  1  1  1  1  1 50  1  1 g9   1  1 10  1  1  1  1  1  1 g10                              1  50   1   1   1   1   1   1 g11                             50   1   1   1   1   1   1   1 g12                              1   1   1   1   1   1   1   1 g13                              1   1   1   1   1   1   1   1 g14                              1   1   1   1   1   1   1   1 g15                              1   1   1   1   1   1   1   1 g16                              1   1   1   1   1   1   1   1 g17                              1   1   1   1   1   1   1   1 ; scalars   a 'max guests at a table' / 4 /   b 'min number of guests known at table' / 2 / variables    g(i,j) 'guest j at table i'    p(i,j,k) 'guest j and k at table i'    z ; binary variable g,p; equations    obj    onetable(j)    capacity(i)    minknown(i,k)    linearize1(i,k)    linearize2(i,j) ; set gt(j,k) 'upper triangle'; gt(j,k)$(ord(k)>ord(j)) = yes; obj..  z =e= sum((i,gt(j,k)), c(j,k)*p(i,j,k)); onetable(j).. sum(i, g(i,j)) =e= 1; capacity(i).. sum(j, g(i,j)) =l= a; minknown(i,k).. sum(j$c(j,k), p(i,j,k)) =g= (b+1)*g(i,k); linearize1(i,k).. sum(j, p(i,j,k)) =l= a*g(i,k); linearize2(i,j).. sum(k, p(i,j,k)) =l= a*g(i,j); model m /all/; option optcr = 0; solve m maximizing z using mip; option g:0; display g.l;

I would probably formulate this slightly different. A linearization

is often formulated as:

Here the last condition can be dropped as we are maximizing the p’s anyway. In general I use these disaggregated versions directly instead of the aggregated versions used in model above.

So how would I write this down? Here is my attempt:

$ontext   Table assignment   This is a reformulation of the original model   Meghan L. Bellows   and J. D. Luc Peterson      Finding an optimal seating chart      http://www.improbable.com/2012/02/12/finding-an-optimal-seating-chart-for-a-wedding/   See also:   http://www.hakank.org/constraint_programming_blog/2011     /03/a_matching_problem_a_related_seating_problem_and_some_other_seating_pr.html $offtext set   t 'tables' /table1*table5/   g 'guests' /g1*g17/ ; alias (g,g1,g2); table c(g1,g2)     g1 g2 g3 g4 g5 g6 g7 g8 g9 g10 g11 g12 g13 g14 g15 g16 g17 g1   1 50  1  1  1  1  1  1  1 g2  50  1  1  1  1  1  1  1  1 g3   1  1  1 50  1  1  1  1 10 g4   1  1 50  1  1  1  1  1  1 g5   1  1  1  1  1 50  1  1  1 g6   1  1  1  1 50  1  1  1  1 g7   1  1  1  1  1  1  1 50  1 g8   1  1  1  1  1  1 50  1  1 g9   1  1 10  1  1  1  1  1  1 g10                              1  50   1   1   1   1   1   1 g11                             50   1   1   1   1   1   1   1 g12                              1   1   1   1   1   1   1   1 g13                              1   1   1   1   1   1   1   1 g14                              1   1   1   1   1   1   1   1 g15                              1   1   1   1   1   1   1   1 g16                              1   1   1   1   1   1   1   1 g17                              1   1   1   1   1   1   1   1 ; scalars   a 'max guests at a table' / 4 /   b 'min number of guests known at table' / 2 / variables    x(g,t)    'guest at table '    meet(g1,g2)  'guests g1 and g2'    meetex(g1,g2,t)  'guests g1 and g2 at table t'    z ; binary variable x,meet,meetex; set gt(g1,g2) 'upper triangle'; gt(g1,g2)$(ord(g2)>ord(g1)) = yes; meet.prior(gt(g1,g2)) = INF; meetex.prior(gt(g1,g2),t) = INF; equations    obj    onetable(g)    capacity(t)    minknown(g)    defmeet(g,g)    linearize1(g,g,t)    linearize2(g,g,t) ; obj..  z =e= sum(gt(g1,g2), c(g1,g2)*meet(g1,g2)); onetable(g).. sum(t, x(g,t)) =e= 1; capacity(t).. sum(g, x(g,t)) =l= a; minknown(g1).. sum(gt(g1,g2)$c(g1,g2), meet(g1,g2)) + sum(gt(g2,g1)$c(g2,g1), meet(g2,g1)) =g= b; defmeet(gt(g1,g2)).. meet(g1,g2) =e= sum(t, meetex(g1,g2,t)); linearize1(gt(g1,g2),t).. meetex(g1,g2,t) =l= x(g1,t); linearize2(gt(g1,g2),t).. meetex(g1,g2,t) =l= x(g2,t); x.fx('g1','table1') = 1; model m /all/; option optcr = 0; solve m maximizing z using mip; option x:0; display x.l;

I renamed some of the sets and variables.

A further improvement is that we fix guest 1 to table 1. This reduces the symmetry in the model.

So which model performs better? Of course this is only one data set, so we need to be careful not to read to much into this, but here are the results with GAMS and Cplex 12.3:

	original model	reformulation
equations	278	1536
variables	1531	902
binary variables	1530	84
optimal objective	226	226
solution time	216 seconds (reported in paper: 2 seconds)	0.4 seconds
iterations/nodes	3502605 iterations, 93385 nodes	6943 iterations, 180 nodes

It looks like the performance of the original model is much slower than reported in the paper. I don’t know the reason for that, may be the GAMS model contained a few tricks not mentioned in the description of the mathematical model (may be related to symmetry when comparing guest j against guest k). Another reason may be that in the paper it is mentioned that some serious server hardware is used while I am running on one thread on a laptop.

Of course this model can also be formulated as a Constraint Programming model. In http://hakank.org/minizinc/wedding_optimal_chart.mzn a single integer variable Tables[guest] for each guest is used indicating the table number. Furthermore using CP constructs one can reduce the model to basically one block of equations:

forall(i in 1..n) ( sum(j in 1..m) (bool2int(tables[j] = i)) >= b /\ sum(j in 1..m) (bool2int(tables[j] = i)) <= a )

In the MIP model we have to do a little bit more work!

Note that the CP formulation is probably incorrect w.r.t. to the minimum number of known people at a table (parameter b).

Update: The CP model is fixed. The advantage of using modeling languages is that other people can read the model. If this would be some C++ code I would not have bothered to try to understand it. Also it is often argued that a modeling language helps in maintaining models as fixes are easier to identify and implement than in a traditional programming language.

xor

It is not often that I can use a XOR in a GAMS model. But here we are..

I am working on some tools for a randomized algorithm for a multi-criteria 0-1 problem. As the algorithm can produce duplicate points we want a simple way to filter these out.

loop(pmax, * generate new solution (dummy solution for now) * assume rounded to 0 or 1     x.l(i) = 1$(uniform(0,1)<0.25); * is this a new solution or a duplicate     dup(p) = not sum(i, x.l(i) xor solpool(p,i));     abort$(card(dup)>1) "Error: solpool contains duplicates"; * if new: add to list * if old: update counter     if(card(dup),         solpool(dup,'count') = solpool(dup,'count') + 1;     else         solpool(pmax,'count') = 1;         solpool(pmax,i) = x.l(i);         p(pmax) = yes;     ); );

The results look like:

----     54 PARAMETER solpool  solution pool of unique solutions               i1          i2          i3          i4          i5       count p1            1                                                           4 p2            1                                   1                       2 p3                                                            1           2 p4                        1                                               2 p5                                    1           1                       1 p7            1                       1                                   1 p8                                                                        2 p9                        1                       1                       2 p13           1           1                                   1           2 p15           1           1           1                                   1 p16                                   1                       1           1

Of course instead of the XOR we could have written:

dup(p) = not sum(i$(x.l(i)<>solpool(p,i)),1);

Difference between parameters and variables

Hi ampl users, I got a new question. Since AMPL does not allow command like "if.... then...", my question is : how to convert the following sentence into a constrain which is acceptable by AMPL. For example, set i set j param a (i,j) var b (i,j) #constrain if b (i,j) > 0, then a (i,j) < 30

If you are using a modeling systems such as AMPL, one of the first concepts you need to understand is the role of parameters and variables. As long as you don’t understand this, there is probably very little you can actually write down correctly.

Here is another example: http://social.msdn.microsoft.com/Forums/en-US/solverfoundation/thread/e5aeecb0-b411-41c9-b2d1-30926290b9ff