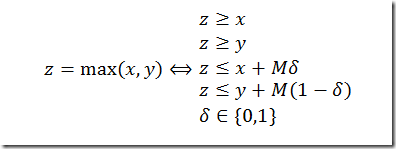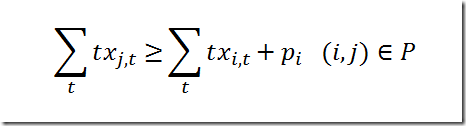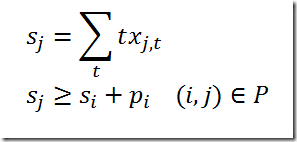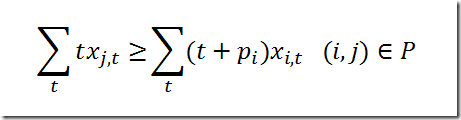Longest flow shop (2)

Permutations in GAMS

This is a follow up to http://yetanothermathprogrammingconsultant.blogspot.com/2012/04/longest-flow-shop.html.

We consider again the small data set:

table proctime(m,j) 'processing times'             job1  job2  job3  job4  job5  job6  job7  job8  job9  job10   machine1   4     2     1     5     4     3     5     2     1     8   machine2   2     5     8     6     7     4     7     3     6     2   machine3   2     8     6     2     2     4     2     7     1     8 ;

This data set comes from:

The first approach to find the permutation with the longest schedule is to enumerate all permutations. GAMS has a built-in option to generate permutations of a set. It is not completely intuitive, in part because the way GAMS stores sets. All sets have fixed ordering with respect to a pool of set elements (the universe). To create a different ordering, an extra index is used. E.g. for 3 jobs we have:

$set n 3 $eval k fact(%n%) set    j           'jobs'                    /job1*job%n%/    p           'permutations'            /p1*p%k%/    allp(p,j,j) 'store all permutations'    m           'processing stage'        /machine1*machine3/ ; option allp>j; option allp:0:1:1; display allp;

The option > creates the permutations. Of course the syntax is not very readable: one would expect a function with a name somehow related to ‘permutation’. One of the major goals when using a modeling system is to produce readable models, and that is certainly not achieved with this syntax.

The result is:

----     13 SET allp  store all permutations INDEX 1 = p1             job1        job2        job3 job1         YES job2                     YES job3                                 YES INDEX 1 = p2             job1        job2        job3 job1         YES job2                                 YES job3                     YES INDEX 1 = p3             job1        job2        job3 job1                     YES job2         YES job3                                 YES INDEX 1 = p4             job1        job2        job3 job1                     YES job2                                 YES job3         YES INDEX 1 = p5             job1        job2        job3 job1                                 YES job2         YES job3                     YES INDEX 1 = p6             job1        job2        job3 job1                                 YES job2                     YES job3         YES

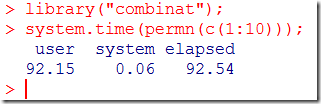
Although I don’t like the syntax, it is actually quite fast. If we set n to 10 and disable the display statement – it would take a long time to print all these permutations – we can generate all 10!=3,628,800 permutations in less than 2.5 seconds. This compares quite good to the following R session:

We can create and evaluate the schedules as follows:

loop(p,    putclose$(mod(ord(p),1000) = 0) "iteration " ord(p):0:0/;    completion(m,j) = 0;    loop((m,allp(p,jj,j)),       completion(m,jj) = max(completion(m,jj-1),completion(m-1,jj)) + proctime(m,j);    );    obj(p) = smax((m,j),completion(m,j)); );

Unfortunately this loop is very slow, it took almost 7 hours on my machine.

Results

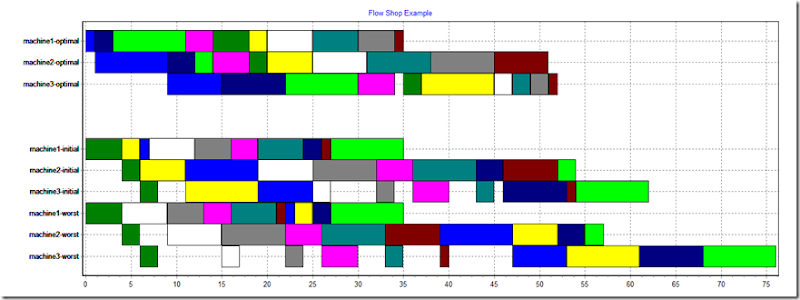
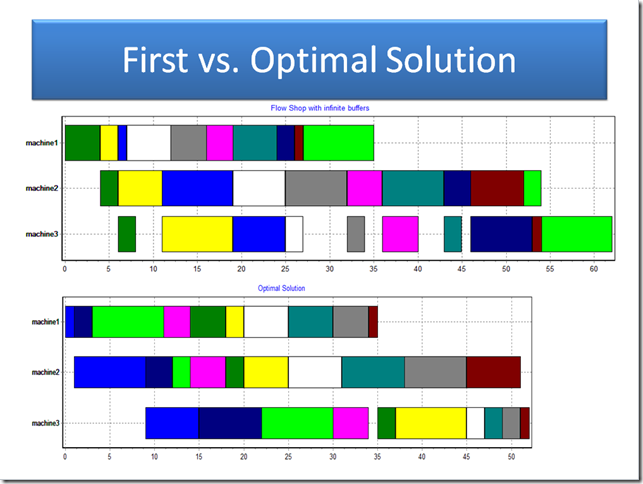
The following picture shows the three schedules we discussed:

• optimal
• initial schedule: formed by sequence job1,job2,job3,…
• a longest schedule

A MIP Formulation

Of course with a little thought we can improve on this solution technique and write a MIP model:

* * assignment constraints * assign1(j).. sum(jj, position(j,jj)) =e= 1; assign2(j).. sum(jj, position(jj,j)) =e= 1; processing(m,j).. completion(m,j) =e= start(m,j) + sum(jj,position(jj,j)*proctime(m,jj)); * * start(m,j) = max(completion(m,j-1),completion(m-1,j)) * max1(m,j)$(ord(j)>1).. start(m,j) =g= completion(m,j-1); max2(m,j)$(ord(m)>1).. start(m,j) =g= completion(m-1,j); max3(m,j)..            start(m,j) =l= completion(m,j-1)+H*b(m,j); max4(m,j)..            start(m,j) =l= completion(m-1,j)+H*(1-b(m,j)); start.fx('machine1','job1')=0; cmaxdef.. cmax =e= completion('machine3','job10'); model flowshop /all/; option optcr=0; solve flowshop maximizing cmax using mip;

It is not 100% trivial as we need to make sure the max is attained exactly. We use the following set of inequalities:

In the case of minimization as formulated in http://yetanothermathprogrammingconsultant.blogspot.com/2012/04/longest-flow-shop.html we just could use bounds as the minimization would make sure that

start(m,j) = max(completion(m,j-1),completion(m-1,j))

would hold exactly (for the places where it matters – if there is slack in some machine this relation may not hold).

This model would look much simpler with a constraint programming formulation. There we could have used constructs like all-different and max to simplify things. Many modern modeling languages support constraint programming (unfortunately GAMS does not). Also note that AMPL using Cplex indicator variables allows this to be formulated quite elegantly (see http://yetanothermathprogrammingconsultant.blogspot.com/2009/07/formulation-ciminaibi.html). GAMS does not directly support indicator variables in the language, but instead some option files must be used.

The above MIP model solves in 0.2 seconds, clearly beating our brute force method.

Longest flow shop

I was trying to demonstrate some simple scheduling models. The permutation flow shop has an obvious first solution: run jobs in the order given in the problem data: job1,job2,job3,…. We compared that with the optimal solution:

The model I presented is fairly simple:

Someone came up with the question: “what would the picture look like for the worst permutation?”.

I think this is actually more difficult to model. We assume in several places that jobs are automatically pushed to the left and if we just start to maximize this won’t work anymore.

Of course just trying all solutions would be feasible in this case. We have 10 jobs so 10! = 3,628,800 permutations (just type 10! in google).

Model is infeasible or unbounded

My favorite return code from an LP/MIP solver is:

MIP status(4): Model was proven to be either infeasible or unbounded.

Come on guys, you really can do better than this! OK, what to do as a user? My simplest suggestion – using GAMS – is to add a bound on the objective variable and solve again:

z.lo=−1e10;
solve m minimizing z using mip;

Now at least we see:

MIP status(3): Model was proven to be infeasible.

If the model was actually unbounded you would have seen large numbers in the solution, making it easy to find out what was wrong.

Note: Please don’t tell me “dual infeasible” is a good return code. That is just another name for the same thing, and just as useless for a modeler. If you are working on a model you really want to know if the model is infeasible or unbounded. I understand it is an easy way out for the algorithm-developer to return something like “dual infeasible” (I have heard some users saying that is just laziness, and I understand that sentiment). The return code should really relate to the model and not what is the easiest for the algorithm-developer to implement.

Not everyone agrees with these opinions (see the comments).

The model was fairly small. If we compare the time both the user needed to email me the question and the model, for me to look at it and respond (say in total half an hour) and the time the solver would need to spend to get a better diagnostic (let’s say 0.1 seconds) then we can say a huge efficiency gain is possible here.

Parallel GAMS jobs (2)

In http://yetanothermathprogrammingconsultant.blogspot.com/2012/04/parallel-gams-jobs.html I described a simple approach I suggested to a client allowing to run multiple scenarios in parallel.

For a different client we needed to run a randomized algorithm that solves many small MIP models. They are so small that using multiple threads inside the MIP solver does not give much performance boost (much of the time is spent outside the pure Branch & Bound part – such as preprocessing etc.). However as the MIP problems are independent of each other we could generate all the necessary data in advance and then call the scenario solver (http://www.gams.com/modlib/adddocs/gusspaper.pdf). This will keep the generated problem in memory, and does in-core updates, so we don’t regenerate the model all the time.

When running the algorithm with n=100,000 MIP models we see the following performance. Note that besides the MIP models there is also a substantial piece of GAMS code that implements other parts of the algorithm.

Implementation	number of MIP models	solve time	rest of algorithm	total time
Traditional GAMS loop (call solver as DLL)	100,000	1068 sec	169 sec	1237 sec
Scenario Solver	100,000	293 sec	166 sec	459 sec

To get more performance I tried to run the scenario solver in parallel. That is not completely trivial as the solver has a number glitches (e.g. scratch files with fixed, hard coded names). I also run parts of the GAMS algorithm in parallel, but some parts had to be done in the master model after merging the results.

Implementation	number of MIP models	Worker threads	parallel sub-problem time	rest of algorithm (serial)	total time
Parallel + Scenario Solver	100,000	4	116 sec	67 sec	183 sec

The implementation does not win the beauty contest, but it could be developed quickly. For these larger problems you always have to watch out for performance bottlenecks. One wrong line in the GAMS model and the performance drops to hours of computation time. In addition the GAMS tools here are not very refined, but if implemented correctly quite effective. As an example consider how I merge the results of the sub jobs. Each sub job writes a results file (GDX file) into its own directory and the master model will read those and merge them together so we have a single solution set for further processing:

* * read and merge the GDX files * loop(job,    put_utility 'gdxin' / 'jobdir',(jobinfo(job,"jobno")):0:0,"\results.gdx"/;    execute_loadpoint solpoollevel,solpoolobj,pp; ) ;

This is not exactly readable and intuitive code (caused by lack of design when these features were added to the GAMS language in a hurry), but it is quite fast. 

Precedence constraints

I often see precedence constraints for time indexed scheduling models formulated as:

Here x(j,t)=1 if job j starts in t (and 0 otherwise). p(i) are the processing times and P is the set of precedence relations.

I would probably write this as:

We add a few variables here but save hopefully some nonzero elements. In addition we may reuse s(j) in other parts of the model.

Now I encountered a formulation like:

I thought about this a little while but I don’t think there is any special advantage to this formulation. (Consider that sum(t,x(i,t))=1).

JavaScript and CMD

In some recent projects I used some JavaScript code. Not sure how useful this is in practice, but here is a neat trick to write and call JavaScript code inside a CMD file: http://blogs.msdn.com/b/joshpoley/archive/2008/01/15/running-jscript-in-a-cmd-file.aspx.

Parallel GAMS jobs

Although GAMS can be used from its IDE, it still has a command line interface. This can be used when calling GAMS from a batch (.cmd) file.

Recently I was asked to speed up running a number of scenarios by exploiting an 8 core machine. As the NLP (actually MCP) models used serial solvers we cannot just use THREADS=8 like when we use MIP solvers such as Cplex or Gurobi. One way to handle this is to write some batch files:

batch1.cmd gams nlpmodel.gms –scenario=1 o=m1.lst lo=2 lf=m1.log gams nlpmodel.gms –scenario=2 o=m2.lst lo=2 lf=m2.log gams nlpmodel.gms –scenario=3 o=m3.lst lo=2 lf=m3.log

Then call these batch files from another batch file:

runall.cmd start batch1.cmd start batch2.cmd start batch3.cmd start batch4.cmd

The START command will start the batch file specified and returns immediately. As a result the batch files batch1.cmd, batch2.cmd, … will run in parallel.

To make this a little bit more configurable we can write a GAMS file that generates these files.

$ontext    course grained parallel solution of optimization jobs $offtext sets    cpu 'processors' /cpu1*cpu7/    j 'jobs' /job1*job60/    assign(cpu,j) /      cpu1.(job1*job8)      cpu2.(job9*job16)      cpu3.(job17*job24)      cpu4.(job25*job33)      cpu5.(job34*job42)      cpu6.(job43*job51)      cpu7.(job52*job60)    / ; abort$sum(j, abs(sum(assign(cpu,j),1)-1) ) "jobs not correctly assigned"; file f /' '/; file g /'runall.cmd'/; loop(cpu, * f = 'batch' + ord(cpu) + '.cmd'   put f;   put_utility 'ren'/ 'batch',ord(cpu):0:0,'.cmd';   loop(assign(cpu,j),       put "call runmodel.cmd ",ord(j):0:0/;   );   putclose "exit"/;   put g,'start batch',ord(cpu):0:0,'.cmd'/; ); putclose g; execute 'runall.cmd';

As we can see here the GAMS syntax around its PUT facility is very ugly (this is one of the parts of GAMS that really urgently needs some redesign). However, ignoring the ugly syntax, it actually generates batch files of the form:

batch2.cmd call runmodel.cmd 9 call runmodel.cmd 10 call runmodel.cmd 11 call runmodel.cmd 12 call runmodel.cmd 13 call runmodel.cmd 14 call runmodel.cmd 15 call runmodel.cmd 16 exit runall.cmd start batch1.cmd start batch2.cmd start batch3.cmd start batch4.cmd start batch5.cmd start batch6.cmd start batch7.cmd

We use 7 cpus and thus 7 parallel jobs here (the idea is to keep one cpu available for normal work).
We are left to implement RUNMODEL.CMD:

runmodel.cmd gams solve.gms r=save1 lo=2 lf=model%1.log o=model%1.lst --scenario=%1

Notes:

1. When running under the IDE you may get a message about the LST (listing) file being used by another process. This is under investigation.

2. GAMS has some new asynchronous calling mechanisms. This does not really improve the above code (adding another put_utility call is never going to look good). For completeness:

$ontext    course grained parallel solution of optimization jobs    using async execute $offtext sets    cpu 'processors' /cpu1*cpu7/    j 'jobs' /job1*job60/    assign(cpu,j) /      cpu1.(job1*job8)      cpu2.(job9*job16)      cpu3.(job17*job24)      cpu4.(job25*job33)      cpu5.(job34*job42)      cpu6.(job43*job51)      cpu7.(job52*job60)    / ; abort$sum(j, abs(sum(assign(cpu,j),1)-1) ) "jobs not correctly assigned"; file f /' '/; loop(cpu, * f = 'batch' + ord(cpu) + '.cmd'   put f;   put_utility 'ren'/ 'batch',ord(cpu):0:0,'.cmd';   put "@echo off"/;   loop(assign(cpu,j),       put "call runmodel.cmd ",ord(j):0:0/;   );   putclose "exit"/;   put_utility 'Exec.Async'/'batch',ord(cpu):0:0,'.cmd'; );