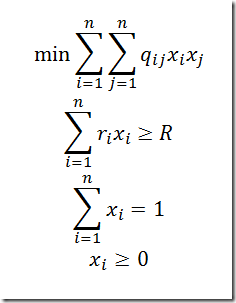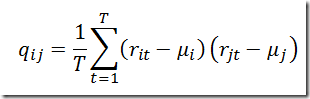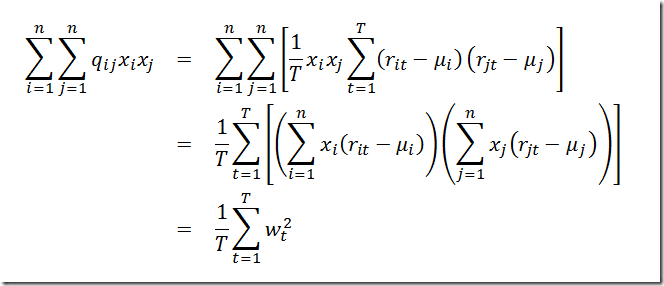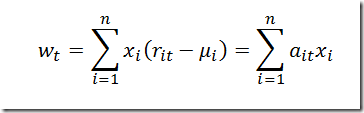This is a simple algorithm to enumerate all (or a subset) of the efficient solutions of an integer programming problem. This is a slightly different approach than used in http://yetanothermathprogrammingconsultant.blogspot.com/2010/02/generating-all-non-dominated-solutions.html. Basically the algorithm is as follows:
- Choose any weights λi > 0
- repeat
- solve problem with weighted obj
- if infeasible: STOP
- record the efficient solution
- add cut to prevent this solution to be found again
- add constraint such that dominated solutions are not accepted
As example we use a simple model from J. Shapiro, “Multiple Criteria Public Investment Decision Making by Mixed Integer Programming”, working paper, MIT, 1975:
max x1+10x2+9x3
max 10x1+x2+9x3
x1+x2+x3 ≤ 2
x1,x2,x3 ∈ {0,1}
The following GAMS model illustrates the algorithm on this small problem:
$ontext
Example (4) from
"Multiple Criteria Public Investment Decision Making by Mixed Integer
Programming", Jeremy F. Shapiro, WP 788-05, Alfred P. Sloan School of
Management, MIT, May 1975
erwin@amsterdamoptimization.com
$offtext
set j /v1,v2,v3/;
binary variables x(j);
set i /obj1,obj2/;
variables z(i),sz;
equations
objs(i)
e
scalobj
;
parameter lambda(i);
table objcoeff(i,j)
v1 v2 v3
obj1 1 10 9
obj2 10 1 9
;
scalobj.. sz =e= sum(i, lambda(i)*z(i));
objs(i).. z(i) =e= sum(j, objcoeff(i,j)*x(j));
e.. sum(j, x(j)) =L= 2;
*
* there are 7 feasible integer solutions
* here we calculate them all
*
equation edummy;
variable dummy;
edummy.. dummy=e=0;
set k/k1*k10/;
set dynk(k) 'dynamic set';
dynk(k) = no;
equation cut(k);
parameter sol(k,j),obj(k,i);
sol(k,j) = 0;
cut(dynk).. sum(j, x(j)$(sol(dynk,j)>0.5) - x(j)$(sol(dynk,j)<0.5)) =l= sum(j$(sol(dynk,j)>0.5),1) - 1;
model m0 /edummy,e,objs,cut/;
option limrow=0, limcol=0;
m0.solprint=2;
m0.solvelink=2;
scalar ok/1/;
loop(k$ok,
solve m0 using mip minimizing dummy;
ok = 1$(m0.modelstat=1 or m0.modelstat=8);
if (ok,
dynk(k) = yes;
sol(k,j) = x.l(j);
obj(k,i) = z.l(i);
);
);
display "----------------------------------------------------",
" All solutions",
"----------------------------------------------------",
sol,obj;
*
* calculate the min and max objectives
*
parameter minz(i), maxz(i);
model m1 /e,objs,scalobj/;
m1.solprint=2;
m1.solvelink=2;
alias (i,ii);
option optcr=0;
loop(ii,
lambda(i) = 0;
lambda(ii) = 1;
solve m1 using mip minimizing sz;
abort$(m1.modelstat<>1) "Not optimal";
minz(ii) = sz.l;
solve m1 using mip maximizing sz;
abort$(m1.modelstat<>1) "Not optimal";
maxz(ii) = sz.l;
);
display "----------------------------------------------------",
" Bounds for objectives",
"----------------------------------------------------",
minz,maxz;
*
* calculate all efficient solutions
* this is a variation on the above:
* a new solution must be better in at least one obj than all previous
* solutions.
*
binary variable y(k,i);
equation nondom(k,i),ysum(k);
nondom(dynk,i).. z(i) =g= obj(dynk,i) - (maxz(i)-minz(i))*(1-y(dynk,i));
ysum(dynk).. sum(i,y(dynk,i)) =g= 1;
model m2 /e,objs,scalobj,cut,nondom,ysum/;
m2.solprint=2;
m2.solvelink=2;
obj(k,i) = 0;
sol(k,j) = 0;
dynk(k) = no;
* any nonzero weight is ok.
lambda(i) = 1/card(i);
ok=1;
loop(k$ok,
solve m2 using mip maximizing sz;
ok = 1$(m2.modelstat=1 or m2.modelstat=8);
if (ok,
dynk(k) = yes;
sol(k,j) = x.l(j);
obj(k,i) = z.l(i);
);
);
display "----------------------------------------------------",
" Efficient/nondominated solutions",
"----------------------------------------------------",
sol,obj;
The first part is optional: we enumerate all feasible integer solutions. This is not possible for large problems, so in practice this step must be omitted. The results for this example:
| ---- 73 ----------------------------------------------------
All solutions
---------------------------------------------------- ---- 73 PARAMETER sol v1 v2 v3 k2 1.000
k3 1.000 1.000
k4 1.000
k5 1.000
k6 1.000 1.000
k7 1.000 1.000 ---- 73 PARAMETER obj obj1 obj2 k2 1.000 10.000
k3 11.000 11.000
k4 10.000 1.000
k5 9.000 9.000
k6 19.000 10.000
k7 10.000 19.000 |
So we have seven possible integer solutions. Note that solution k1 is v1=v2=v3=0, obj1=obj2=0. Many of them are dominated. E.g. solution k4 is dominated by solution k3 (note: we are maximizing).
In the model we need a big-M constant. To find good values for these constants we need to find the minimum and maximum values for each objective. That is done in part 2. The result is:
| ---- 98 ----------------------------------------------------
Bounds for objectives
---------------------------------------------------- ---- 98 PARAMETER minz ( ALL 0.000 ) ---- 98 PARAMETER maxz obj1 19.000, obj2 19.000 |
This means we can use 19 as big-M value.
In the last part we enumerate all efficient or non-dominated solutions:
| ---- 140 ----------------------------------------------------
Efficient/nondominated solutions
---------------------------------------------------- ---- 140 PARAMETER sol v1 v2 v3 k1 1.000 1.000
k2 1.000 1.000
k3 1.000 1.000 ---- 140 PARAMETER obj obj1 obj2 k1 10.000 19.000
k2 19.000 10.000
k3 11.000 11.000 |
For very large problems we can make the set k sufficiently small so that we collect k non-dominated solutions instead of all possible non-dominated solutions. Note that the problem becomes larger and larger. The number of constraints added to the problem in each cycle is:
- 1 cut to exclude this solution
- (K+1) constraints to find non dominated solutions (here K is the number of objectives).
In addition we add each cycle K binary variables.
It is noted that the weights are not very important when we are able to find all efficient solutions. Just any nonzero weights will do.