Finding a cluster of closest points

Problem statement

From [1]:

Consider \(n=100\) points in an 12 dimensional space. Find \(m=8\) points such that they are as close as possible.

Models

The problem can be stated as a simple MIQP (Mixed Integer Quadratic Programming) model.

 

MINSUM MIQP Model
\[\begin{align} \min & \sum_{i\lt j} \color{darkred}x_i \cdot \color{darkred}x_j \cdot \color{darkblue}{\mathit{dist}}_{i,j} \\ & \sum_i \color{darkred}x_i = \color{darkblue}m \\ & \color{darkred}x_i \in \{0,1\} \end{align}\]

This is a simple model. The main wrinkle is that we want to make sure that we only count each distance once. For this reason, we only consider distances with \(i \lt j\). Of course, we can exploit this also in calculating the distance matrix \( \color{darkblue}{\mathit{dist}}_{i,j}\), and make this a strictly upper-triangular matrix. This saves time and memory.

As the \( \color{darkred}x\) variables are binary, we can easily linearize this problem:

MINSUM MIP Model
\[\begin{align} \min & \sum_{i\lt j} \color{darkred}y_{i,j} \cdot \color{darkblue}{\mathit{dist}}_{i,j} \\ & \color{darkred}y_{i,j} \ge \color{darkred}x_i + \color{darkred}x_j - 1 && \forall i \lt j\\ & \sum_i \color{darkred}x_i = \color{darkblue}m \\ & \color{darkred}x_i \in \{0,1\} \\ &\color{darkred}y_{i,j} \in [0,1] \end{align}\]

The inequality implements the implication \[\color{darkred}x_i= 1 \textbf{ and } \color{darkred}x_j = 1 \Rightarrow \color{darkred}y_{i,j} = 1 \] The variables \(\color{darkred}y_{i,j}\) can be binary or can be relaxed to be continuous between 0 and 1. The MIQP and MIP model should deliver the same results. 

Finally, we can also consider a slightly different problem. Instead of minimizing the sum of the distances between points inside the cluster of the selected points, we can also minimize the maximum distance between points inside the cluster. The (linear) model can look like:

MINMAX MIP Model
\[\begin{align} \min\> & \color{darkred}z \\ & \color{darkred}z \ge \color{darkred}y_{i,j} \cdot \color{darkblue}{\mathit{dist}}_{i,j} && \forall i \lt j \\ & \color{darkred}y_{i,j} \ge \color{darkred}x_i + \color{darkred}x_j - 1 && \forall i \lt j\\ & \sum_i \color{darkred}x_i = \color{darkblue}m \\ & \color{darkred}x_i \in \{0,1\} \\ &\color{darkred}y_{i,j} \in [0,1] \end{align}\]

We re-use our linearization here.

Finally, I also tried a very simple greedy heuristic:

1. Select the two points that are closest to each other.
2. Select a new unselected point that is closest to our already selected points.
3. Repeat step 2 until we have selected 8 points.

We can expect our optimization models to do a bit better than this simplistic approach. 

In our methods here, we did not make any assumptions about the distance metric being used We just needed the distance matrix. This means you can use Euclidean, Manhattan, or other metrics. In addition, you can use some normalization or weighting before calculating the distances. This may be useful if the features have different units. These models also do not change whether one uses low- or high-dimensional data.

There are alternative models one could envision, such as finding the smallest enclosing sphere or box. These methods do not make things simpler and will likely not improve upon our models. 

Small data set

Let's start with selecting \(m=8\) points from  \(n=50\), using random 2d coordinates.

----     10 PARAMETER coord  coordinates

                  x           y

point1        0.172       0.843
point2        0.550       0.301
point3        0.292       0.224
point4        0.350       0.856
point5        0.067       0.500
point6        0.998       0.579
point7        0.991       0.762
point8        0.131       0.640
point9        0.160       0.250
point10       0.669       0.435
point11       0.360       0.351
point12       0.131       0.150
point13       0.589       0.831
point14       0.231       0.666
point15       0.776       0.304
point16       0.110       0.502
point17       0.160       0.872
point18       0.265       0.286
point19       0.594       0.723
point20       0.628       0.464
point21       0.413       0.118
point22       0.314       0.047
point23       0.339       0.182
point24       0.646       0.561
point25       0.770       0.298
point26       0.661       0.756
point27       0.627       0.284
point28       0.086       0.103
point29       0.641       0.545
point30       0.032       0.792
point31       0.073       0.176
point32       0.526       0.750
point33       0.178       0.034
point34       0.585       0.621
point35       0.389       0.359
point36       0.243       0.246
point37       0.131       0.933
point38       0.380       0.783
point39       0.300       0.125
point40       0.749       0.069
point41       0.202       0.005
point42       0.270       0.500
point43       0.151       0.174
point44       0.331       0.317
point45       0.322       0.964
point46       0.994       0.370
point47       0.373       0.772
point48       0.397       0.913
point49       0.120       0.735
point50       0.055       0.576

The MINSUM MIQP and MIP model gives the same solution, but (as expected) the MINMAX model is slightly different. Here are the results with Cplex:

 

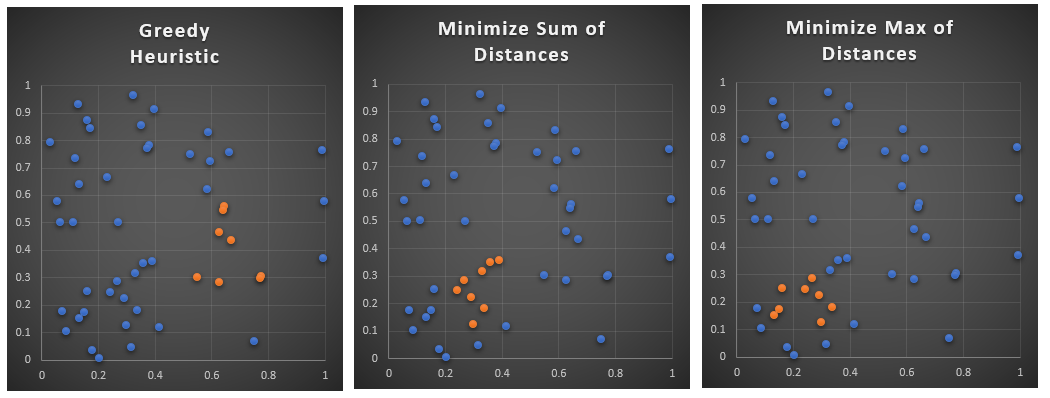
          HEURISTIC        MIQP         MIP      MINMAX

point2        1.000
point3                    1.000       1.000       1.000
point9                                            1.000
point10       1.000
point11                   1.000       1.000
point12                                           1.000
point15       1.000
point18                   1.000       1.000       1.000
point20       1.000
point23                   1.000       1.000       1.000
point24       1.000
point25       1.000
point27       1.000
point29       1.000
point35                   1.000       1.000
point36                   1.000       1.000       1.000
point39                   1.000       1.000       1.000
point43                                           1.000
point44                   1.000       1.000
status                  Optimal     Optimal     Optimal
obj                       3.447       3.447       0.210
sum           4.997       3.447       3.447       3.522
max           0.291       0.250       0.250       0.210
time                     33.937       2.125       0.562

When we plot the results, we see:

Obviously, our optimization models do much better than the heuristic. Two optimization models have quite an overlap in the selected points. To compare the objectives MINSUM and MINMAX we can plot them against each other:

Obviously, our heuristic is not doing that great.

Large data set 

Here we select \(m=8\) points from  \(n=100\), using random 12d coordinates. Using Gurobi on a faster machine we see:

----    112 PARAMETER results  

          HEURISTIC        MIQP         MIP      MINMAX

point5        1.000                               1.000
point8                    1.000       1.000
point17       1.000                               1.000
point19                   1.000       1.000
point24                                           1.000
point35                   1.000       1.000
point38                   1.000       1.000
point39                                           1.000
point42       1.000                               1.000
point43                                           1.000
point45       1.000       1.000       1.000
point51       1.000
point56       1.000
point76       1.000
point81                   1.000       1.000
point89                   1.000       1.000
point94       1.000       1.000       1.000       1.000
point97                                           1.000
status                TimeLimit     Optimal     Optimal
obj                      26.230      26.230       1.147
sum          30.731      26.230      26.230      27.621
max           1.586       1.357       1.357       1.147
time                   1015.984      49.000       9.594
gap%                     23.379

The MINSUM MIQP model hit a time limit of 1000 seconds but actually found the optimal solution. It just did not have the time to prove it. The overlap between the MINSUM models and the MINMAX model is very small (just one shared point). I expected more overlap.

Conclusions

The MINMAX model seems to solve faster than the MINSUM versions. This is a little bit surprising: often these max or min objectives are slower than direct sums. It always pays off to do some experiments with different formulations. Slightly different models can show a large difference in solution times. This is a great example of that.

These models are independent of the dimensionality of the data and the distance metric being used.

References

1. Given a set of points or vectors, find the set of N points that are closest to each other, https://stackoverflow.com/questions/64542442/given-a-set-of-points-or-vectors-find-the-set-of-n-points-that-are-closest-to-e

Appendix: GAMS code

Some interesting features:

• There are not that many models where I can use xor operators. Here it is used in the Greedy Heuristic where we want to consider points \(i\) and \(j\) where one of them is in the cluster and one outside. 
• Of course instead of the condition that x.l(i) xor x.l(j) is nonzero, we also could have required that x.l(i)+x.l(j)=1. I just could not resist the xor.
• Macros are used to prevent repetitive code in the reporting of results.
• Acronyms are used in reporting. 

$ontext   find cluster of m=8 points closest to each other   compare:        simple greedy heuristic (HEURISTIC)        quadratic model (MIQP)        linearized model (MIP)        minmax model (MINMAX) $offtext set   c 'coordinates' /x,y/   i 'points' /point1*point50/ ; scalar m 'number of points to select' /8/; parameter coord(i,c) 'random coordinates'; coord(i,c) = uniform(0,1); display coord; alias(i,j); set ij(i,j) 'upper triangular structure'; ij(i,j) = ord(i) < ord(j); parameter dist(i,j) 'euclidean distances'; dist(ij(i,j)) = sqrt(sum(c, sqr(coord(i,c)-coord(j,c)))); binary variables x(i) 'selected points'; positive variable y(i,j) 'x(i)*x(j), relaxed to be continuous'; y.up(ij)=1; variable z 'objective'; equations     obj1  'quadratic objective'     obj2  'linearized objective'     obj3  'minmax objective'     select 'number of selected points'     bound  'implication x(i)=x(j)=1 ==> y(i,j)=1' ; obj1.. z =e= sum(ij(i,j), x(i)*x(j)*dist(ij)); obj2.. z =e= sum(ij, y(ij)*dist(ij)); obj3(ij).. z =g= y(ij)*dist(ij); select.. sum(i, x(i)) =e= m; bound(ij(i,j))..  y(i,j) =g= x(i) + x(j) - 1; model m1 /obj1,select/; model m2 /obj2,select,bound/; model m3 /obj3,select,bound/; option optcr=0,mip=cplex,miqcp=cplex,threads=8; *------------------------------------------------ * reporting macros *------------------------------------------------ parameter results(*,*); set dummy 'ordering for output' /  status, obj, sum, max, time, 'gap%' /; acronym TimeLimit; acronym Optimal; * macros for reporting $macro sumdist    sum(ij(i,j), x.l(i)*x.l(j)*dist(ij)) $macro maxdist    smax(ij(i,j), x.l(i)*x.l(j)*dist(ij)) $macro report(m,label)  \     x.l(i) = round(x.l(i));  \     results(i,label) = x.l(i); \     results('status',label)$(m.solvestat=1) = Optimal; \     results('status',label)$(m.solvestat=3) = TimeLimit; \     results('obj',label) = z.l; \     results('sum',label) = sumdist; \     results('max',label) = maxdist; \     results('time',label) = m.resusd; \     results('gap%',label)$(m.solvestat=3) = 100*abs(m.objest - m.objval)/abs(m.objest); *------------------------------------------------ * heuristic *------------------------------------------------ * step 1 : select points 1 and 2 by minimizing distance scalar dmin,dmin1,dmin2; dmin = smin(ij,dist(ij)); loop(ij(i,j)$(dist(ij)=dmin),    x.l(i)=1;    x.l(j)=1;    break; ); * add points 3..m, closest to points selected earlier scalar k; for(k = 3 to m,    dmin = smin(ij(i,j)$(x.l(i) xor x.l(j)), dist(ij));    loop(ij(i,j)$(dist(ij)=dmin),      x.l(i)=1;      x.l(j)=1;      break;    ); ); results(i,'HEURISTIC') = x.l(i); results('sum','HEURISTIC') = sumdist; results('max','HEURISTIC') = maxdist; *------------------------------------------------ * run models m1 through m3 *------------------------------------------------ solve m1 minimizing z using miqcp; report(m1,'MIQP') solve m2 minimizing z using mip; report(m2,'MIP') solve m3 minimizing z using mip; report(m3,'MINMAX') display results;

Solution methods for linear bilevel problems

For some classes of problems, it is a strategy to form explicit KKT optimality conditions and convert the resulting complementarity conditions to big-M constraints. In case the original problem was linear (or in some cases quadratic), the resulting model is a MIP model. One such application is solving non-convex QP models [1]. Another application is a bilevel LP, where we reformulate the inner problem by stating the optimality conditions for the inner-problem. In [2], such a problem is given: 

bilevel LP
\[\begin{align}\max\> &\color{darkred}z = \color{darkred}x+\color{darkred}y \\ & \color{darkred}x \in [0,2] \\ & \min \>\color{darkred}y\\ & \qquad \color{darkred}y \ge 0 \perp \color{darkred} \lambda_1 \\ & \qquad \color{darkred}x - 0.01\color{darkred}y \le 1 \perp \color{darkred}\lambda_2 \end{align} \]

The notation \(\perp\) indicates the name of the dual variable for the inner constraints. After the inner problem is converted to optimality conditions, we have:

Inner LP as optimality conditions

\[\begin{align}\max\> & \color{darkred}z = \color{darkred}x+\color{darkred}y \\ & \color{darkred}x \in [0,2]\\ & 1 - \color{darkred}\lambda_1 - 0.01 \color{darkred}\lambda_2 = 0 \\ & \color{darkred}y \ge 0 \\ & \color{darkred}x - 0.01\color{darkred}y \le 1\\ & \color{darkred}\lambda_1 \cdot \color{darkred}y = 0 \\ & \color{darkred}\lambda_2 \cdot \left( \color{darkred}x -0.01\color{darkred}y - 1 \right) = 0 \\ & \color{darkred}\lambda_1,\color{darkred}\lambda_2\ge 0 \end{align} \]

The products can be interpreted as an "or" condition. These can be linearized using binary variables and big-M constraints:

Linearized problem

\[\begin{align}\max\> & \color{darkred}z = \color{darkred}x+\color{darkred}y \\ & \color{darkred}x \in [0,2]\\ & 1 - \color{darkred}\lambda_1 - 0.01 \color{darkred}\lambda_2 = 0 \\ & \color{darkred}y \ge 0 \\ & \color{darkred}x - 0.01\color{darkred}y \le 1\\ & \color{darkred}\lambda_1 \le \color{darkblue} M_1^d \color{darkred}\delta_1 \\ & \color{darkred}y \le \color{darkblue} M_1^p (1-\color{darkred}\delta_1) \\ & \color{darkred}\lambda_2 \le \color{darkblue} M_2^d \color{darkred}\delta_2 \\ & -\color{darkred}x +0.01\color{darkred}y + 1 \le \color{darkblue} M_2^p (1-\color{darkred}\delta_2) \\ & \color{darkred}\lambda_1,\color{darkred}\lambda_2\ge 0 \\ & \color{darkred}\delta_1,\color{darkred}\delta_2 \in \{0,1\} \end{align} \]

The letters \(p\) and \(d\) in the big-M constants indicate primal and dual.  Note that we flipped the sign of the second constraint of the inner problem. This was to make \(\color{darkred}\lambda_2\) a non-negative variable.

Choosing big-M values

One big issue is: choose appropriate values for the big-M constants. The values \(\color{darkblue} M_1^d,\color{darkblue} M_1^p,\color{darkblue} M_2^d,\color{darkblue} M_2^p = 200\) are valid bounds on \(\color{darkred}\lambda_1, \color{darkred}y, \color{darkred}\lambda_2, -\color{darkred}x +0.01\color{darkred}y + 1\). This gives the solution:

                           LOWER          LEVEL          UPPER

---- VAR x                   .             2.0000         2.0000      
---- VAR y                   .           100.0000        +INF         
---- VAR lambda1             .              .            +INF         
---- VAR lambda2             .           100.0000        +INF         
---- VAR delta1              .              .             1.0000      
---- VAR delta2              .             1.0000         1.0000      
---- VAR z                 -INF          102.0000        +INF         

The problem of choosing the right big M values is important. Choosing values that are too small, can lead to cutting off optimal values. Big-M values that are too large have other problems such as numerical issues and trickle flow. In [2] it is argued that many modelers use the following algorithm to detect if a big-M value is too small:

1. Select initial values for \( \color{darkblue} M_j^d,  \color{darkblue} M_j^p \).
2. Solve the linearized MIP model.
3. Look for binding big-M constraints that should be inactivated. If not found, stop: we have found the optimal solution.
4. Increase the corresponding big-M value.
5. Go to step 2.

Unfortunately, this is algorithm is not guaranteed to work. [2] gives an example: use as starting values \(\color{darkblue} M_j^d = 50, \color{darkblue} M_j^p = 200\). The solution looks like:

                           LOWER          LEVEL          UPPER

---- VAR x                   .             2.0000         2.0000      
---- VAR y                   .              .            +INF         
---- VAR lambda1             .             1.0000        +INF         
---- VAR lambda2             .              .            +INF         
---- VAR delta1              .             1.0000         1.0000      
---- VAR delta2              .             1.0000         1.0000      
---- VAR z                 -INF            2.0000        +INF         

The values \(\color{darkred}\delta_j=1\) indicate we should look at the constraints: \(\color{darkred}\lambda_j \le \color{darkblue}M_j^d\). As \(\color{darkred}\lambda_1=1, \color{darkred}\lambda_2=0\) these are not binding. Hence, the erroneous conclusion is that this solution is optimal. 

Our conclusion is: we cannot reliably detect that big-M values are chosen too small by searching for binding constraints.

Alternatives

In [3], it is argued that SOS1 (special ordered sets of type 1) variables should be used instead of binary variables. For our example, this means we would replace our big-M constraints by: 

SOS1 representation
\[\begin{align} & \color{darkred}\lambda_1, \color{darkred}y \in SOS1 \\ & \color{darkred}\lambda_2, \color{darkred}s \in SOS1 \\ &\color{darkred}s = -\color{darkred}x+0.01\color{darkred}y+1 \\ & \color{darkred}s \ge 0 \end{align} \]

Many MIP solvers (but not all) support SOS1 variables. Binary variables can sometimes be faster, but SOS1 variables have the advantage that no big-M constants are needed. The same can be said for indicator constraints. A formulation using indicator constraints can look like:

 

Indicator constraints

\[\begin{align} & \color{darkred} \delta_1 = 0 \Rightarrow \color{darkred}\lambda_1 =0 \\ & \color{darkred} \delta_1 = 1\Rightarrow \color{darkred}y = 0 \\ & \color{darkred} \delta_2 = 0 \Rightarrow \color{darkred}\lambda_2 = 0 \\ & \color{darkred} \delta_2 = 1 \Rightarrow \color{darkred}x-0.01\color{darkred}y = 1 \\ & \color{darkred}x-0.01\color{darkred}y \le 1 \\ & \color{darkred} \delta_1,\color{darkred}\delta_2 \in \{0,1\} \end{align} \]

We can also solve the quadratic model directly using global solvers like Antigone, Baron, Couenne, or Gurobi. Sometimes reasonable bounds are needed to help globals solvers.

It is noted that the GAMS EMP tool can generate the quadratic model for you. I still had to specify to use a global solver for it to find the optimal solution.

Conclusion

Instead of using big-M constraints to handle complementarity conditions in linear bi-level optimization problems, there are a few alternatives:

• SOS1 variables
• Indicator constraints
• Global solvers for non-convex quadratic problems

References

1. Solving non-convex QP problems as a MIP,  https://yetanothermathprogrammingconsultant.blogspot.com/2016/06/solving-non-convex-qp-problems-as-mip.html 
2. Salvador Pineda and Juan Miguel Morales, Solving Linear Bilevel Problems Using Big-Ms: Not All That Glitters Is Gold, September 2018,  https://arxiv.org/pdf/1809.10448.pdf
3. Thomas Kleinert and Martin Schmidt, Why there is no need to use a big-M in linear bilevel optimization: A computational study of two ready-to-use approaches, October 2020,  http://www.optimization-online.org/DB_FILE/2020/10/8065.pdf 

Appendix: GAMS Code

$ontext    different formulations of a bilevel optimization problem.    model 1. high level model solved as EMP model    max x + y    st        x in [0,2]        min y        st  y >= 0        : lambda1 >= 0            x-0.01y <= 1  : lambda2 >= 0    Note: in subsequent model we flip the last constraint to make the sign of the dual >= 0    This model can be solved using EMP + a global solver. $offtext option optcr=0; positive variables x,y; x.up = 2; variables    z 'outer objective'    zin 'inner objective' ; equations    obj     'outer objective'    objin   'inner objective'    cin1     'inner constraint 1'    cin2     'inner constraint 2' ; obj..     z =e= x+y; objin..   zin =e= y; cin1..    y =g= 0; cin2..    x-0.01*y =l= 1; model m1 /obj, objin, cin1, cin2/; $onecho > "%emp.info%" bilevel x min zin y objin cin1 cin2 $offecho $onecho > jams.opt subsolver couenne $offecho m1.optfile=1; solve m1 using EMP maximizing z; $ontext    model 2. Optimality conditions for inner problem.       This is a non-convex quadratic model.        This can be solved with Gurobi, Couenne, Baron, Antigone.    max x + y    st        x in [0,2]        1 - lambda1 - 0.01*lambda2 = 0        lambda1*y = 0        lambda2*(-x+0.01y+1) = 0        lambda1,lambda2>=0 $offtext positive variables lambda1,lambda2; equations    dLdy    'derivative of lagrangean'    quad1   'complementarity constraint (quadratic)'    quad2   'complementarity constraint (quadratic)' ; dLdy..  1 - lambda1 - 0.01*lambda2 =e= 0; quad1.. lambda1*y =e= 0; quad2.. lambda2*(x-0.01*y-1) =e= 0; model m2 /obj,dLdy,cin2,quad1,quad2/; option minlp = couenne; solve m2 using minlp maximizing z; $ontext    model 3. Linearized version of model 2 using big-M constraints    max x + y    st        x in [0,2]        1 - lambda1 - 0.01*lambda2 = 0        lambda1 <= delta1*M1d        y <= (1-delta1)*M1p        lambda2 <= delta2*M2d        -x+0.01y+1 <= (1-delta2)*M2p        lambda1,lambda2>=0        delta1, delta2 binary $offtext binary variable delta1, delta2; equations    comp1d  'linearized complementarity constraint (dual)'    comp1p  'linearized complementarity constraint (primal)'    comp2d  'linearized complementarity constraint (dual)'    comp2p  'linearized complementarity constraint (primal)' ; scalars    M1p  'big-M for primal' /200/    M1d  'big-M for dual'   /200/    M2p  'big-M for primal' /200/    M2d  'big-M for dual'   /200/ ; comp1d.. lambda1 =l= delta1*M1d; comp1p.. y =l= (1-delta1)*M1p; comp2d.. lambda2 =l= delta2*M2d; comp2p.. -x+0.01*y+1 =l= (1-delta2)*M2p; model m3 /obj,dLdy,comp1d,comp1p,comp2d,comp2p/; solve m3 using mip maximizing z; $ontext    model 4. Linearized version of model 2 using SOS1 variables    max x + y    st        x in [0,2]        1 - lambda1 - 0.01*lambda2 = 0        s = -x+0.01y+1        lambda1,lambda2,s >=0        lambda1, y forms a SOS1 set        lambda2, s forms a SOS1 set     In GAMS we need to reformulate this a bit as SOS1 variables are indexed.     No need for s in the GAMS model. $offtext set k 'SOS members' /k1,k2/; sos1 variable    sos_1(k)  'for the pair lambda1, y'    sos_2(k)  'for the pair lambda2, -x+0.01y+1' ; equations   sos_1a  'assign to sos1 member'   sos_1b  'assign to sos1 member'   sos_2a  'assign to sos1 member'   sos_2b  'assign to sos1 member' ; sos_1a.. y =e= sos_1('k1'); sos_1b.. lambda1 =e= sos_1('k2'); sos_2a.. -x+0.01*y+1 =e= sos_2('k1'); sos_2b.. lambda2 =e= sos_2('k2'); model m4 /obj,dLdy,sos_1a,sos_1b, sos_2a, sos_2b/; solve m4 using mip maximizing z; $ontext    model 5. Linearized version of model 2 using indicator constraints    this is very ugly in GAMS    max x + y    st        x in [0,2]        1 - lambda1 - 0.01*lambda2 = 0        x - 0.01y <= 1        d1 = 0 ==> lambda1 = 0        d1 = 1 ==> y = 0        d2 = 0 ==> lambda2 = 0        d2 = 1 ==> x - 0.01y = 1        lambda1, lambda2 >= 0        d1, d2 in {0,1}        y >= 0 $offtext binary variables    d1   'lambda1 = 0 OR y = 0'    d2   'lambda2 = 0 OR x - 0.01y = 1' ; equations    d10 'part of indicator constraint'    d11 'part of indicator constraint'    d20 'part of indicator constraint'    d21 'part of indicator constraint'    dummy 'make sure d1,d2 are part of the model' ; d10.. lambda1 =e= 0; d11.. y =e= 0; d20.. lambda2 =e= 0; d21.. x-0.01*y =e= 1; dummy.. d1+d2 =g= 0; $onecho > cplex.opt indic d10$d1 0 indic d11$d1 1 indic d20$d2 0 indic d21$d2 1 $offecho model m5 /obj,dLdy,d10,d11,d20,d21,cin2,dummy/; m5.optfile = 1; solve m5 using mip maximizing z;