For a scheduling that I could not solve in one swoop I tried to develop a small algorithm. Basically: schedule the m<n jobs that come first, then fix the m jobs and schedule the next m jobs. This seems to work with Cplex. The algorithm looks like:
loop(k,
j(j0) = kj(k,j0);
solve sched minimizing makespan using mip;
report(k,'obj') = sched.objval;
report(k,'modelstat') = sched.modelstat;
report(k,'solvestat') = sched.solvestat;
xstart.fx(j,t) = xstart.l(j,t);
); |
This algorithm will perform the following:
| 1-10 | 11-20 | 21-30 | 31-40 | 41-50 |
| solved | | | | |
| fixed | solved | | | |
| fixed | fixed | solved | | |
| fixed | fixed | fixed | solved | |
| fixed | fixed | fixed | fixed | solved |
For Cplex we get:
| ---- 180 PARAMETER report obj modelstat solvestat k1 1480.000 1.000 1.000
k2 2940.000 1.000 1.000
k3 4400.000 1.000 1.000
k4 5860.000 1.000 1.000
k5 7320.000 1.000 1.000
|
However for Gurobi we get:
| ---- 180 PARAMETER report obj modelstat solvestat k1 1480.000 1.000 1.000
k2 2940.000 1.000 1.000
k3 4400.000 1.000 1.000
k4 19.000 1.000
k5 19.000 1.000
|
It turns out that the fixing of a solution causes the next iteration to be infeasible. We can actually isolate step k3 and do:
solve m minimizing makespan using mip;
xstart.fx(j,t) = xstart.l(j,t);
solve m minimizing makespan using mip; |
This will make the second model infeasible: i.e. Gurobi does not like its own solution! In this case it is a tolerance question: the final solution is slightly infeasible. We can fix this by:
loop(k,
j(j0) = kj(k,j0);
solve m minimizing makespan using mip;
report(k,'obj') = m.objval;
report(k,'modelstat') = m.modelstat;
report(k,'solvestat') = m.solvestat;
xstart.fx(j,t) = round(xstart.l(j,t));
);
|
because we know all job step times are in whole seconds. Now both Cplex and Gurobi can solve the problem just fine.
A reasonable good solution looks like:
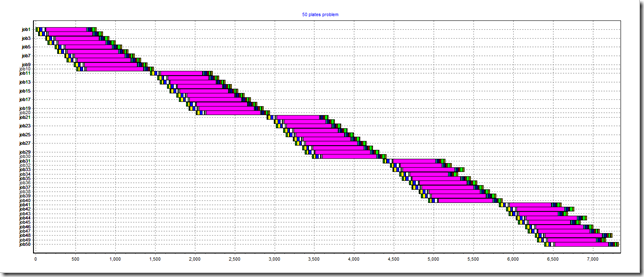
By accident our algorithmic batch size is the same as the batch size for a good solution (this is not required for the algorithm to work).
The solution is somewhat sensitive where we put the breaks when decomposing the model. This may indicate a rolling horizon algorithm may work better (see http://yetanothermathprogrammingconsultant.blogspot.com/2008/06/rolling-horizon-implementation-in-gams.html).
