Permutations in GAMS
This is a follow up to http://yetanothermathprogrammingconsultant.blogspot.com/2012/04/longest-flow-shop.html.
We consider again the small data set:
| table proctime(m,j) 'processing times' job1 job2 job3 job4 job5 job6 job7 job8 job9 job10 machine1 4 2 1 5 4 3 5 2 1 8 machine2 2 5 8 6 7 4 7 3 6 2 machine3 2 8 6 2 2 4 2 7 1 8 ; |
This data set comes from:
The first approach to find the permutation with the longest schedule is to enumerate all permutations. GAMS has a built-in option to generate permutations of a set. It is not completely intuitive, in part because the way GAMS stores sets. All sets have fixed ordering with respect to a pool of set elements (the universe). To create a different ordering, an extra index is used. E.g. for 3 jobs we have:
| $set n 3 $eval k fact(%n%) set j 'jobs' /job1*job%n%/ p 'permutations' /p1*p%k%/ allp(p,j,j) 'store all permutations' m 'processing stage' /machine1*machine3/ ; option allp>j; option allp:0:1:1; display allp; |
The option > creates the permutations. Of course the syntax is not very readable: one would expect a function with a name somehow related to ‘permutation’. One of the major goals when using a modeling system is to produce readable models, and that is certainly not achieved with this syntax.
The result is:
| ---- 13 SET allp store all permutations INDEX 1 = p1 job1 job2 job3 job1 YES INDEX 1 = p2 job1 job2 job3 job1 YES INDEX 1 = p3 job1 job2 job3 job1 YES INDEX 1 = p4 job1 job2 job3 job1 YES INDEX 1 = p5 job1 job2 job3 job1 YES INDEX 1 = p6 job1 job2 job3 job1 YES |
Although I don’t like the syntax, it is actually quite fast. If we set n to 10 and disable the display statement – it would take a long time to print all these permutations – we can generate all 10!=3,628,800 permutations in less than 2.5 seconds. This compares quite good to the following R session:
We can create and evaluate the schedules as follows:
| |
Unfortunately this loop is very slow, it took almost 7 hours on my machine.
Results
The following picture shows the three schedules we discussed:
- optimal
- initial schedule: formed by sequence job1,job2,job3,…
- a longest schedule
A MIP Formulation
Of course with a little thought we can improve on this solution technique and write a MIP model:
| * model flowshop /all/; |
It is not 100% trivial as we need to make sure the max is attained exactly. We use the following set of inequalities:
In the case of minimization as formulated in http://yetanothermathprogrammingconsultant.blogspot.com/2012/04/longest-flow-shop.html we just could use bounds as the minimization would make sure that
start(m,j) = max(completion(m,j-1),completion(m-1,j))
would hold exactly (for the places where it matters – if there is slack in some machine this relation may not hold).
This model would look much simpler with a constraint programming formulation. There we could have used constructs like all-different and max to simplify things. Many modern modeling languages support constraint programming (unfortunately GAMS does not). Also note that AMPL using Cplex indicator variables allows this to be formulated quite elegantly (see http://yetanothermathprogrammingconsultant.blogspot.com/2009/07/formulation-ciminaibi.html). GAMS does not directly support indicator variables in the language, but instead some option files must be used.
The above MIP model solves in 0.2 seconds, clearly beating our brute force method.

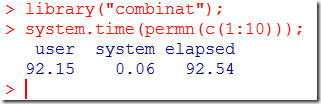


As a comparison, on a Core i5 M480 (2.67 GHz) generating all permutations using the C++ built-in next_permutation takes about 0.5 seconds. The code is about as long as the GAMS code, but is much more readable.
ReplyDelete1. GAMS also creates a (sparse) data-structure and stores all permutations (these are the sets p and allp in the example). So that is a little bit of extra work. But clearly: handwritten C/C++ can often beat a GAMS implementation.
ReplyDelete2. When we solve the MIP formulation, we are even faster than C/C++ generating only the permutations.
I know that GAMS does a lot more; the comparison was not meant to say that C++ is "better". Given that the C++-code is very simple and uses a very good permutation generation algorithm, I thought it would be interesting to compare to see what one pays for using GAMS.
ReplyDeleteAs for solving the actual problem (which may very well be larger than 10 and thus out of reach of brute force permutations), I also think that constraint programming is suitable.