From http://groups.google.com/group/ampl/browse_thread/thread/7c849e1de871b22b:
| Dear all, I would like to know how to model the property of symmetry in AMPL. For example, how can I tell AMPL that x [1,3] and x [3,1] is the same Best Regards |
| If x is a variable, something like the following: set N; # index set Paul |
I would like to add that anytime I see something like this, there is a possibility to exploit such a feature.
If x[i,j] is symmetric we can reduce the size of x by only considering the (lower or upper) triangular part of x. This is the case both when x is a variable or when x is a parameter. An example for exploiting this in a variable is documented here: http://yetanothermathprogrammingconsultant.blogspot.com/2012/02/weddings-and-optimal-seating.html. The set gt(g1,g2) is used many times here to reduce the size of variable meet(g1,g2).
A well known example of symmetric data is the portfolio optimization problem. If the variance-covariance matrix is large and dense it certainly helps to consider only half of it. Here is a way to exploit a symmetric Q matrix which can be used in many QP models with x’Qx in the objective:
Even if Q is not symmetric we can make it symmetric by something like q(i,j) = 0.5(q(i,j)+q(j,i)).
Of course one could argue that MIP solvers and their presolvers are getting smarter and we don’t need this anymore. This is indeed sometimes the case for the better solvers. However, for larger instances we should not only consider the solver but also time spent in generating the model. Often these tricks can make a significant impact on overall performance and total turnaround time of jobs.
Some computational evidence is here regarding a large portfolio QP model (synthetic dataset with 2K instruments):
As you can see Cplex does not really care whether QP is full or triangular (the small difference in time is related to reading the Q data: there is more data when Q is full). However GAMS is twice as fast when we use a triangular Q. Aside from this it is noted that GAMS is not very fast compared to Cplex on these models. The processing of the nonlinear terms is relatively expensive.
For completeness I want to mention that for this portfolio optimization problem there is an alternative formulation using the mean adjusted returns directly. This formulation leads to a QP with a diagonal Q matrix. The timings for the same data set are:
GAMS benefits greatly from this easier formulation, but also Cplex is faster.
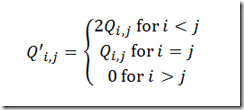


No comments:
Post a Comment