| $ontext
Some (s,Q) inventory models
We evaluate two inventory models:
(1) Cost per Stockout Event (CSOE) Model
(2) Cost per Item Short (CIS) Model
It is sometimes suggested to input Q*=EOQ into these models
opposed to optimizing directly for Q. Here we try to
see how much a difference this makes.
$offtext
scalars
D 'mean demand ($/year)' /62000/
sigma_D 'standard deviation of demand' /8000/
c 'cost per item ($/item)' /100/
cK 'order cost ($/order)' /3270.9678/
ci 'annual inventory cost'
h 'holding charge (% of unit cost)' /0.15/
mu_dl 'mean over lead time'
sigma_dl 'sigma over lead time'
L 'lead time (days)' /14/
B1 'CSOE penalty' /50000/
cs 'Item short cost' /45/
Qeoq 'EOQ'
;
ci = h*c;
mu_dl = D/(365/L);
sigma_dl = sigma_D/sqrt(365/L);
parameter results(*,*,*);
*------------------------------------------------------
* Deterministic EOQ model
*------------------------------------------------------
variables
tc 'total cost'
Q 'order quantity'
;
* prevent division by zero
Q.lo = 0.1;
equations
costdef1 'total cost calculation for simple deterministic case'
;
costdef1..
tc =e= c*D + cK*(D/Q) + ci*(Q/2);
model eoq /costdef1/;
solve eoq minimizing tc using nlp;
Qeoq = Q.l;
results('EOQ','Q','EOQ') = Qeoq;
*------------------------------------------------------
* Cost per Stockout Event Model
*------------------------------------------------------
positive variables
k
PStockout 'P[x>=k]'
s 'order point'
;
equations
costdef2 'CSOE total cost function'
cdf 'this implements P[x>=k]'
sdef 'calculation of order point s'
;
costdef2..
tc =e= c*D + cK*(D/Q) + ci*(Q/2+k*sigma_dl) + B1*(D/Q)*PStockOut;
cdf..
Pstockout =e= 1-errorf(k);
sdef..
s =e= mu_dl + k*sigma_dl;
model csoe /costdef2,cdf,sdef/;
*------------------------------------------------------
* Cost per Item Short (CIS) Model
*------------------------------------------------------
variables
G 'unit loss function'
;
equations
costdef3 'CIS total cost function'
Gdef 'this implements G(k)'
;
costdef3..
tc =e= c*D + cK*(D/Q) + ci*(Q/2+k*sigma_dl) + cs*sigma_dl*G*(D/Q);
Gdef..
G =e= 1/sqrt(2*pi)*exp(-0.5*sqr(k)) - k * (1-errorf(k));
model cis /costdef3,sdef,Gdef/;
*------------------------------------------------------
* Results with Q endogenous
*------------------------------------------------------
solve csoe minimizing tc using nlp;
results('CSEO','Total Cost','Qendog') = TC.L;
results('CSEO','Inv+Short Cost','Qendog') = TC.L-c*D;
results('CSEO','Q','Qendog') = Q.L;
results('CSEO','s','Qendog') = s.L;
results('CSEO','k','Qendog') = k.L;
solve cis minimizing tc using nlp;
results('CIS','Total Cost','Qendog') = TC.L;
results('CIS','Inv+Short Cost','Qendog') = TC.L-c*D;
results('CIS','Q','Qendog') = Q.L;
results('CIS','k','Qendog') = k.L;
results('CIS','s','Qendog') = s.L;
*------------------------------------------------------
* Results with Q fixed to EOQ
*------------------------------------------------------
Q.fx = Qeoq;
solve csoe minimizing tc using nlp;
results('CSEO','Total Cost','Qeoq') = TC.L;
results('CSEO','Inv+Short Cost','Qeoq') = TC.L-c*D;
results('CSEO','Q','Qeoq') = Q.L;
results('CSEO','k','Qeoq') = k.L;
results('CSEO','s','Qeoq') = s.L;
solve cis minimizing tc using nlp;
results('CIS','Total Cost','Qeoq') = TC.L;
results('CIS','Inv+Short Cost','Qeoq') = TC.L-c*D;
results('CIS','Q','Qeoq') = Q.L;
results('CIS','k','Qeoq') = k.L;
results('CIS','s','Qeoq') = s.L;
display results;
|
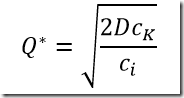
No comments:
Post a Comment