More on network models (2)

Re: http://yetanothermathprogrammingconsultant.blogspot.com/2011/08/more-on-network-models.html.

What if you go bigger? Here some results with two of the leading commercial LP solvers (using default settings) compared to GAMS:

LP solution times are a little bit more unpredictable (in this case this is positive: somewhat quicker than thought by extrapolating from first picture in more-on-network-models.html), but GAMS execution time (including generation time) is still nicely linear.

Shipping problem

I am starting to work on a problem that looks like a shipping problem I worked on earlier: garments (shirts) are sent from China to stores in the US either directly in a number of packages containing standard contents or through a US warehouse. The cheapest is to send the standard boxes from China but as there are just a few standard configurations, stores will need to be supplied with additional shirts from the US warehouse. Shirts come in different sizes.

The basic model looked like:

All quantities with bars are parameters (constants). Even though this is a simple model it was not completely trivial to get good solutions:

• The model as presented is an MINLP. We linearized to make it a MIP.
• The data set was rather large because of a large number of stores.
• We could preprocess the demand data as some stores have the same demand; this reduced the size by about a third. We added weights to the objective to represent how many times a demand pattern was used.
• In practice over-supplying a store was expensive, so we can fix OverShipped(Store,Size)=0.
• It was not practical to solve this model in one swoop. We found good solutions by first finding a good content for a single standard box, and then (after fixing the content of this first box) finding a good proposal for a second standard box. Adding more standard boxes was not reducing the objective by much.
• The set sizes can also include other attributes such as color etc.

Bin Packing

For pure bin packing problems some really good heuristics exist. For the problem illustrated in http://www.developerfusion.com/article/5540/bin-packing/ one of the best solutions is:

So if we solve to optimality, do we gain a lot? From http://en.wikipedia.org/wiki/Bin_packing_problem is looks doubtful. Indeed when I solve:

$ontext    Bin packing example $offtext sets    b 'bins' /bin1*bin19/    i 'items' /item1*item45/ ; scalar binsize /80/; parameter itemsize(i) /   item1   26, item2   57, item3   18, item4    8, item5   45   item6   16, item7   22, item8   29, item9    5, item10  11   item11   8, item12  27, item13  54, item14  13, item15  17   item16  21, item17  63, item18  14, item19  16, item20  45   item21   6, item22  32, item23  57, item24  24, item25  18   item26  27, item27  54, item28  35, item29  12, item30  43   item31  36, item32  72, item33  14, item34  28, item35   3   item36  11, item37  46, item38  27, item39  42, item40  59   item41  26, item42  41, item43  15, item44  41, item45  68 /; variables    x(i,b)  'assignment'    y(b)    'whether bin is used'    z       'count used bins' ; binary variable x,y; * relax y: automatically integer y.prior(b) = INF; equations    onebin(i)    cap(b)    binusd    obj    symmetry(b) ; onebin(i)..    sum(b, x(i,b)) =e= 1; cap(b)..       sum(i, x(i,b)*itemsize(i)) =l= binsize; binusd(i,b)..  y(b) =g= x(i,b); obj..          z =e= sum(b, y(b)); symmetry(b+1)..  y(b) =g= y(b+1); model m1 /onebin,cap,binusd,obj/; model m2 /onebin,cap,binusd,obj,symmetry/; option optcr=0; solve m1 minimizing z using mip;

we get an optimal solution with 17 bins.

Of course as discussed in http://yetanothermathprogrammingconsultant.blogspot.com/2011/07/scheduling-of-tv-advertisement-theory.html my real models are almost always much more complicated than shown in these stylized bin packing examples. In those cases a MIP-based solution algorithm can be even more worthwhile than a (simple) heuristic as there is more room for improvement. In the real case we dealt with a complicated multi-objective model where our model seems to outperform the heuristic in almost all objectives. This is the case even after the heuristic was improved using some fine-tuning after looking at our solutions.

More on network models

I received some additional questions on solving some very large network models. Basically we used the formulation presented here: http://yetanothermathprogrammingconsultant.blogspot.com/2011/06/network-formulation.html. A slightly more optimized version is shown below:

$ontext   large sparse max flow network example   Performance       nodes  arcs    gams       solver                      execution  time       1k     10k     0.031      0.045       2k     20k     0.047      0.112       5k     50k     0.156      0.286       10k   100k     0.343      1.125   Erwin Kalvelagen,   Amsterdam Optimization,   erwin@amsterdamoptimization.com $offtext $set n 10000 option limrow=0, limcol=0, solprint=off; sets   i   source(i)   sink(i) ; alias(i,j); parameter capacity(i,j) 'capacity, but also defines network'; $gdxin network%n% $loaddc i source sink capacity abort$(card(source)<>1) "We want one source node"; abort$(card(sink)<>1) "We want one sink node"; set arcs(i,j) 'we have an arc if capacity<>0'; arcs(i,j)$capacity(i,j) = yes; scalar narcs 'number of arcs'; narcs = card(arcs); display narcs; parameter rhs(i); rhs(source) = -1; rhs(sink) = 1; variables   x(i,j) 'flow along arcs'   f      'total flow' ; positive variables x; x.up(arcs) = capacity(arcs); equations    flowbal(i) 'flow balance' ; flowbal(i)..    sum(arcs(j,i), x(j,i)) - sum(arcs(i,j), x(i,j)) =e= f*rhs(i); model m /flowbal/; solve m maximizing f using lp; display f.l;

The performance of GAMS looks very good. GAMS execution time scales slightly better than the LP solver used to solve the problem:

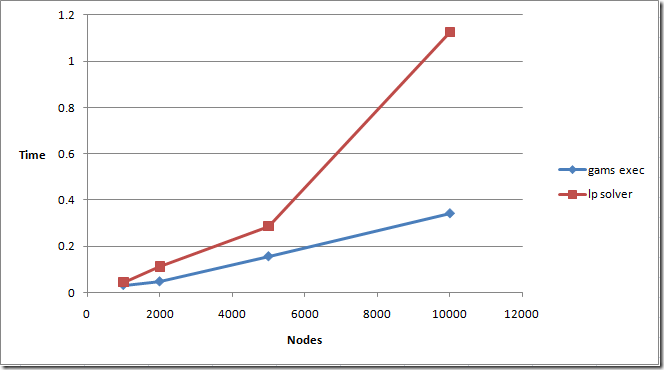
GAMS almost scales linearly with the number of nonzero elements to be generated. In this case that means linearly with the number of nodes (because the number of nonzeroes is equal to 10*nodes in these models).

The main difference with the earlier model is that we replaced:

x.up(i,j) = capacity(i,j);

by

x.up(arcs) = capacity(arcs);

This actually saves some time and memory. In the first case we set many x.up’s to zero even though they are not used in the model. These variables with non-default bounds will need to be created and use up memory. In the second case, we only touch variables that are really used.

This small change makes a lot of difference for larger models. For n=5k we see GAMS execution time decrease from 3.775 seconds to 0.156 seconds. If things get large one needs to pay attention to detail!

AMPL Version

A direct translation to AMPL can look like:

set nodes; set source within nodes; set sink within nodes; param capacity {(i,j) in (nodes cross nodes)}, default 0; set arcs within (nodes cross nodes) := {i in nodes, j in nodes: capacity[i,j]}; # version 1 : slow calc of arcs # set arcs := {i in nodes, j in nodes: capacity[i,j]};                                   # version 2 : slow calc of x # set arcs within (nodes cross nodes);                                                    # version 3 : fast, read from data file param rhs{i in nodes} := if i in source then -1 else if i in sink then +1; var x {(i,j) in arcs} >= 0, <= capacity[i,j]; var f; maximize obj:f; subject to flowbal{i in nodes}:    sum{(j,i) in arcs} x[j,i] - sum{(i,j) in arcs} x[i,j] = f*rhs[i];

This formulation is not handled very efficiently by AMPL: the timings for n=5k are

##genmod times: ##seq      seconds    cum. sec.    mem. inc.  name ## 77            0            0            0  derstage ## 81            0            0            0  sstatus ## 95            0            0            0  nodes ## 96            0            0            0  source ## 97            0            0            0  sink ## 98            0            0            0  capacity ## 99      10.4521      10.4521   1146012664  arcs ## 100            0      10.4521            0  rhs ## 101    0.0156001      10.4677        65544  x ## 103            0      10.4677            0  f ## 105            0      10.4677            0  obj ## 107    0.0624004      10.5301      4148296  flowbal

Especially the calculation of the set arcs is expensive.

Note that if we use an alternative for arcs:

set arcs := {i in nodes, j in nodes: capacity[i,j]};

the burden is moved to x:

##genmod times: ##seq      seconds    cum. sec.    mem. inc.  name ## 77            0            0            0  derstage ## 81            0            0            0  sstatus ## 95            0            0            0  nodes ## 96            0            0            0  source ## 97            0            0            0  sink ## 98            0            0            0  capacity ## 99            0            0            0  arcs ## 100            0            0            0  rhs ## 101      10.5301      10.5301   1147323392  x ## 103            0      10.5301            0  f ## 105            0      10.5301            0  obj ## 107    0.0780005      10.6081      4147928  flowbal

When we run a few different instances we see we do something causing non-linear scaling:

It is clear this is not a good approach. We need to do something about this set arcs. In AMPL we don’t really need to calculate this set, we can directly populate this from the data by replacing in the data file:

param: capacity := n1 n32 87 n1 n37 44 n1 n124 38 …

by

param: arcs : capacity := n1 n32 87 n1 n37 44 n1 n124 38 …

Now we get the set arcs basically for free, and we get linear scaling:

The total AMPL generation time vs. LP solution time is here:

This is very close to the GAMS timings given that this was on a different machine.

GLPK

The open source tool GLPK can handle many AMPL linear models. However, in some cases it is substantial slower. This model demonstrates this behavior. We run the model as:

C:\projects\tmp>timeit \Projects\glpk\glpk\bin\glpsol.exe -m network.mod -d network1000.dat Reading model section from network.mod... network.mod:24: warning: unexpected end of file; missing end statement inserted 24 lines were read Reading data section from network1000.dat... network1000.dat:10108: warning: unexpected end of file; missing end statement inserted 10108 lines were read Generating obj... Generating flowbal... Model has been successfully generated lpx_simplex: original LP has 1001 rows, 10001 columns, 20003 non-zeros lpx_simplex: presolved LP has 1000 rows, 10001 columns, 20002 non-zeros lpx_adv_basis: size of triangular part = 999 *     0:   objval =  0.000000000e+000   infeas =  0.000000000e+000 (1) *   171:   objval =  4.780000000e+002   infeas =  0.000000000e+000 (1) OPTIMAL SOLUTION FOUND Time used:   0.1 secs Memory used: 13.4M (14073536 bytes) Version Number:   Windows NT 6.0 (Build 6002) Exit Time:        0:32 am, Thursday, August 4 2011 Elapsed Time:     0:00:05.563 Process Time:     0:00:05.600 System Calls:     160954 Context Switches: 89933 Page Faults:      20453 Bytes Read:       248437 Bytes Written:    87315 Bytes Other:      130434 C:\projects\tmp>

Besides being much slower than AMPL, the performance of the model generation phase is showing more than linear scaling:

Model generation is here calculated as total elapsed time minus time used for the LP solver.

My conclusions:

1. AMPL and GAMS are capable of generating simple network models faster than a good LP solver can solve them
2. But a simple mistake and performance goes down the drain
3. Direct translations between GAMS and AMPL models are not always a good idea.