MIQP vs MIP

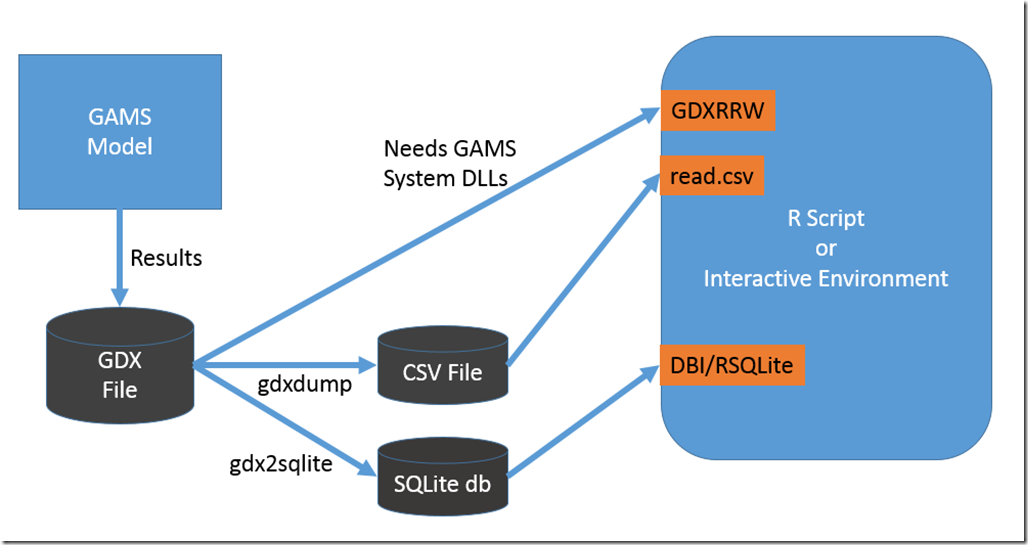
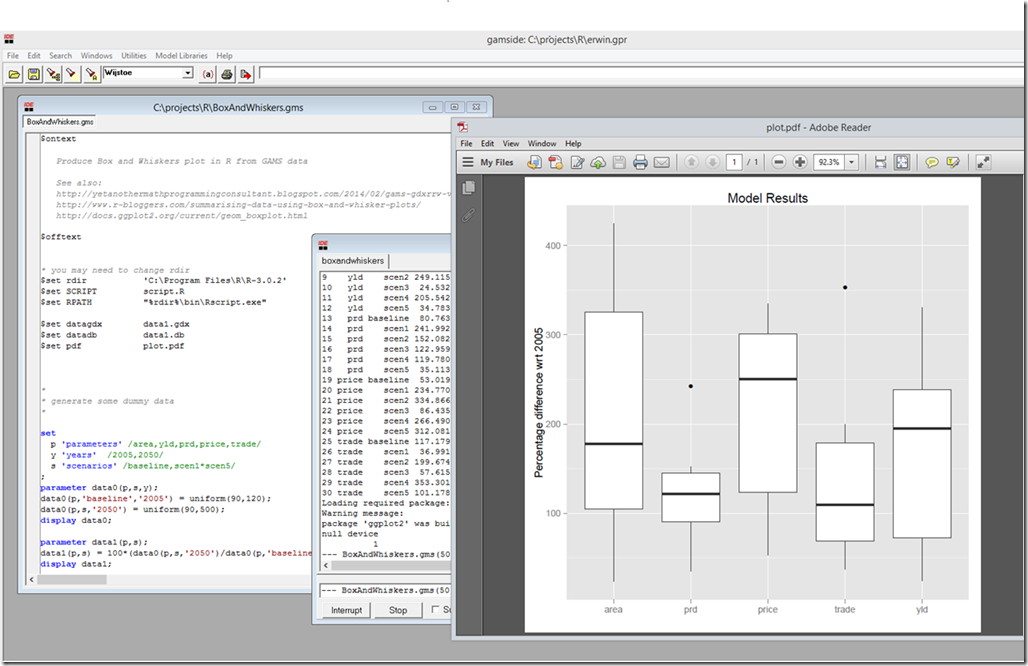
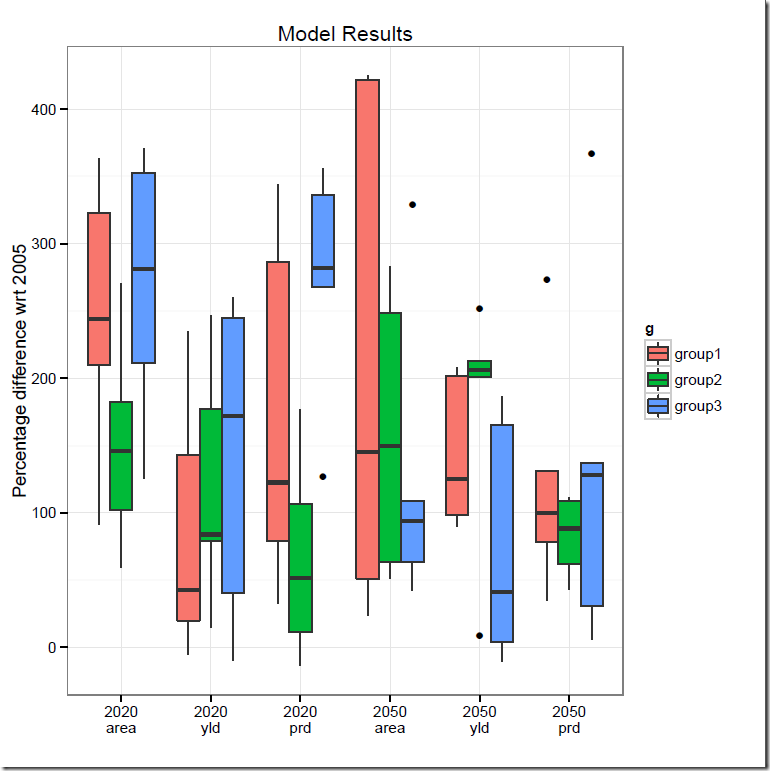
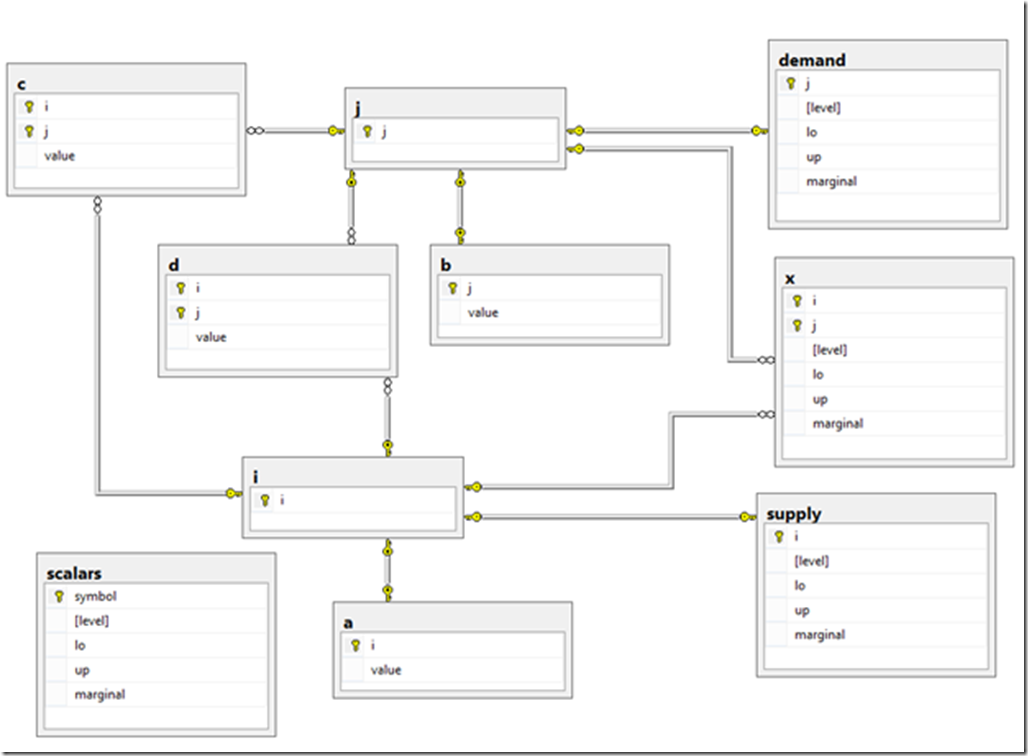
On my experience many MIQP models can and should be reformulated into straight linear MIP models. The reason is threefold: MIQP solvers are not as reliable as MIP solvers (they can experience numerical difficulties much more often), they can not solve many QPs that are not convex and the performance of a corresponding MIP model can be much better.

An example of this was discussed in https://groups.google.com/forum/#!topic/gurobi/t-N23d24uuw.

With some larger data sets (randomly generated), I saw the following:

Scip (MIQP formulation) was stopped when exceeding 1000 seconds.

This is a non-trivial reformulation, so the presolvers are not (yet) able to replicate this.

PS. In general I don’t think it is a good idea to skimp on variables and equations as is suggested in the discussion. Often we see poorly formulated models as a result of trying to save on variables and constraints, resulting in models that are much denser and actually more difficult to solve. From the above numbers we can see my liberal use of variables and equations in the MIP formulation does not really harm and actually this formulation is light years ahead in terms of performance and reliability compared to the original MIQP formulation.

GAMS to Python

When we need to export data from GAMS to Python for further processing, I often use SQLite as intermediate storage. It is very easy to load data from SQLite into a Pandas dataframe:

 

The text_factory thing may help with Unicode issues.

Compare this to reading the same data into R:

For more info about doing data stuff in Python see:

Data manipulation in GAMS, R or SQL

When moving data from GAMS to R via SQLite we have three possible spots where we can apply some data manipulation:

Suppose we want to plot some data but need to do:

Here is the code in GAMS:

I could do the same thing in R, but the code is slightly more messy:

The final attempt is in SQL, which is not too bad either (but with nested queries more complicated than the GAMS version):

 

In all cases we did not use any loops.

Generating Box Plots from GAMS

Of course using R’s ggplot2 package. Used gdx2sqlite to pass on data from GAMS to R. See also: R Maps from GAMS,

Newer version:

Experiment: Database Diagram of GAMS model

It is always helpful to look at your model in a different way. Not sure if this is a very useful tool in practice. But it may help when passing on data from a GAMS model to a DBA as a documentation tool.

Sets        i   canning plants   / seattle, san-diego /        j   markets          / new-york, chicago, topeka / ;   Parameters        a(i)  capacity of plant i in cases          /    seattle     350               san-diego   600  /        b(j)  demand at market j in cases          /    new-york    325               chicago     300               topeka      275  / ;   Table d(i,j)  distance in thousands of miles                     new-york       chicago      topeka       seattle          2.5           1.7          1.8       san-diego        2.5           1.8          1.4  ;   Scalar f  freight in dollars per case per thousand miles  /90/ ;   Parameter c(i,j)  transport cost in thousands of dollars per case ;             c(i,j) = f * d(i,j) / 1000 ;   Variables        x(i,j)  shipment quantities in cases        z       total transportation costs in thousands of dollars ;   Positive Variable x ;   Equations        cost        define objective function        supply(i)   observe supply limit at plant i        demand(j)   satisfy demand at market j ;   cost ..        z  =e=  sum((i,j), c(i,j)*x(i,j)) ;   supply(i) ..   sum(j, x(i,j))  =l=  a(i) ;   demand(j) ..   sum(i, x(i,j))  =g=  b(j) ;   Model transport /all/ ;   Solve transport using lp minimizing z ;   Display x.l, x.m ;

When do two intervals overlap?

For a scheduling tool I encountered the following problem. For a set of intervals generate a list of a pairs that overlap. For those pairs (A,B) I can generate a constraint (Note: we are smart and do not generate both x_A+x_B≤1 and x_B+x_A≤1) The test if two intervals A=[a₁,a₂], B=[b₁,b₂] overlap is:

or

depending on borderline cases (the last version is called the “strict” version in the following). Here is the demonstration:

Note that if the intervals are determined endogenously in the model, we often write “no-overlap” constraints for two intervals A=[a₁,a₂], B=[b₁,b₂] as:

I.e. B starts after A ends or A starts after B ends. Indeed, we can see that

which derives our second “strict” form of the overlap conditions.