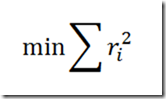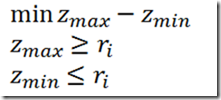Don’t always trust what a solver is saying

This is supposed to be a fairly difficult MIQP. However, when I run it I get quickly: INFEASIBLE:

Tried aggregator 2 times. MIQP Presolve eliminated 1 rows and 1 columns. MIQP Presolve modified 248 coefficients. Aggregator did 52 substitutions. Reduced MIQP has 125 rows, 548 columns, and 3696 nonzeros. Reduced MIQP has 496 binaries, 0 generals, 0 SOSs, and 0 indicators. Reduced MIQP objective Q matrix has 52 nonzeros. Presolve time =    0.00 sec. Probing time =    0.00 sec. Clique table members: 654. MIP emphasis: balance optimality and feasibility. MIP search method: dynamic search. Parallel mode: none, using 1 thread. Tried aggregator 1 time. No QP presolve or aggregator reductions. Presolve time =    0.00 sec. Parallel mode: none, using 1 thread for barrier Number of nonzeros in lower triangle of A*A' = 2360 Using Approximate Minimum Degree ordering Total time for automatic ordering = 0.00 sec. Summary statistics for Cholesky factor:   Rows in Factor            = 125   Integer space required    = 241   Total non-zeros in factor = 3007   Total FP ops to factor    = 90075 Itn      Primal Obj        Dual Obj  Prim Inf Upper Inf  Dual Inf             0  1.4172319e+007 -1.4172911e+007 2.45e+003 5.04e+002 2.77e+007    1  1.2037355e+007  1.0009350e+007 1.78e+002 3.66e+001 2.01e+006    2  1.1903244e+007  1.1658232e+007 2.15e+001 4.42e+000 2.43e+005    3  1.1888608e+007  1.1839300e+007 4.33e+000 8.90e-001 4.89e+004    4  1.1885153e+007  1.1882071e+007 2.71e-001 5.56e-002 3.05e+003    5  1.1884924e+007  1.1884909e+007 1.33e-003 2.73e-004 1.50e+001 Barrier time =    0.05 sec. Total time on 1 threads =    0.05 sec. Root relaxation solution time =    0.05 sec.         Nodes                                         Cuts/    Node  Left     Objective  IInf  Best Integer    Best Bound    ItCnt     Gap       0     0    infeasible                                          5         Root node processing (before b&c):   Real time             =    0.05 Sequential b&c:   Real time             =    0.00                           ------- Total (root+branch&cut) =    0.05 sec. MIQP status(119): integer infeasible or unbounded Problem is integer infeasible. **** SOLVER STATUS     1 Normal Completion         **** MODEL STATUS      10 Integer Infeasible       **** OBJECTIVE VALUE               NA

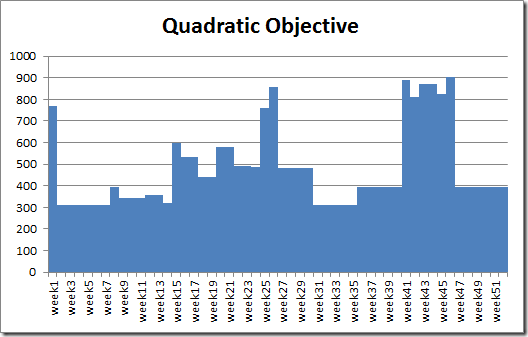
OK, but that sounds not really correct. I found a good integer solution with a linearized objective (same constraints). So lets fix the integer variables and see what happens:

* solve MIP
solve gms1 minimizing z using mip;
* fix integer variables
x.fx(i,t) = x.l(i,t);
* and feed it into MIQP solver
solve gms2 minimizing z using miqcp;

Now I see:

Tried aggregator 1 time. MIQP Presolve eliminated 178 rows and 601 columns. All rows and columns eliminated. Presolve time =    0.00 sec. MIQP status(101): integer optimal solution Fixing integer variables, and solving final QP.. Tried aggregator 1 time. QP Presolve eliminated 178 rows and 601 columns. All rows and columns eliminated. Presolve time =    0.00 sec. Total time on 1 threads =    0.00 sec. QP status(1): optimal Proven optimal solution. MIP Solution:     14817439.000000    (0 iterations, 0 nodes) Final Solve:      14817439.000000    (0 iterations)

Hmm, so not integer infeasible after all. Some more experiments yielded:

• Using MIPSTART with the MIP solution allowed the MIQP solver to proceed
• Scaling the objective cause the MIQP to proceed also. The scaling looks like:
  objective2.. z =e= sum(t,sqr(reserves(t)))/1e6;

Don’t always trust the messages from the solvers…

GAMS qp interface not very coherent

It is possible to write quadratically constrained problems (and QPs in particular) in GAMS and solve them efficiently with solvers like Cplex, Gurobi. But the rules are somewhat ad-hoc and incoherent.

1. GAMS will not extract a QCP when using the notation x**2 (for a rather obscure reason; this should probably be dealt with in a smarter way)
2. GAMS will extract a QCP with the notation x*x or sqr(x) or power(x,2)
3. But GAMS will again not allow power(x,1) or power(x,0) so we can’t write the following:

sets   g 'generators' /g1,g2/   d 'degree'   /d0,d1,d2/ ; table cfuelcost(g,d)  'coefficients for fuel cost as quadratic function of output.'       d2        d1       d0 g1    0.00889   10.333   200 g2    0.00741   10.833   240 ; parameter v(d); v(d) = ord(d)-1; variables    p(g)      'output'    fuelcost  'total fuel cost' ; positive variable p; equations    efuel    'fuel consumption constraint' ; * power(x,2) is allowed * power(x,1) or power(x,0) is not recognized????? *efuel.. fuelcost =e= sum(g, cfuelcost(g,'d2')*power(p(g),2) + cfuelcost(g,'d1')*p(g) + cfuelcost(g,'d0')); efuel.. fuelcost =e= sum((g,d), cfuelcost(g,d)*power(p(g),v(d))); model m /all/; option qcp=cplex; solve m using qcp minimizing fuelcost;

In forbidden cases you’ll get the poorly worded error message:

*** Could not load data from file: Detected 1 general nonlinear rows in model

Smoothing

In a scheduling model for maintenance of power generators the objective is to smooth the reserves. The authors use a quadratic objective to model and the results over a year look like:

  

MIQP’s still solve significantly slower than MIP models, so I was looking for a linear approximation. The first thing that comes to mind is to minimize the max. This gives:

The problem here is we get a few weeks with really low reserves. An alternative is to minimize the difference between the max and the min. This looks like:

This actually looks quite similar to the first picture, and we have achieved our goal: make the model linear.

1 vs 4 threads

Running a small MIP using 1 thread:

Optimize a model with 177 rows, 549 columns and 3800 nonzeros Presolve time: 0.02s Presolved: 177 rows, 549 columns, 3944 nonzeros Variable types: 1 continuous, 548 integer (496 binary) Found heuristic solution: objective 949.0000000 Root relaxation: objective 4.990000e+02, 947 iterations, 0.03 seconds     Nodes    |    Current Node    |     Objective Bounds      |     Work Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time      0     0  499.00000    0   63  949.00000  499.00000  47.4%     -    0s      0     0  499.00000    0   93  949.00000  499.00000  47.4%     -    0s      0     0  499.00000    0   63  949.00000  499.00000  47.4%     -    0s      0     2  499.00000    0   63  949.00000  499.00000  47.4%     -    0s H  135   117                     910.0000000  499.00000  45.2%  47.3    0s *  204    96              44     901.0000000  499.00000  44.6%  47.1    0s   1963   797  891.00000   34   53  901.00000  578.12129  35.8%  46.1    5s   6122  2135  822.02658   39   78  901.00000  720.84013  20.0%  34.5   10s  12502  3801     cutoff   44       901.00000  796.00000  11.7%  27.4   15s  21404  5575  891.00000   51   42  901.00000  862.00000  4.33%  21.7   20s  34494  6391  891.00000   42   53  901.00000  891.00000  1.11%  17.1   25s  52100  4430  891.00000   67   60  901.00000  891.00000  1.11%  12.8   31s  68445  3439     cutoff   72       901.00000  891.00000  1.11%  10.7   35s  94101  2702 infeasible   56       901.00000  891.00000  1.11%   8.9   40s 115791  2055     cutoff   55       901.00000  891.00000  1.11%   8.0   45s 141811  1165  891.00000   40   81  901.00000  891.00000  1.11%   7.2   50s 168722   165  891.00000   44   59  901.00000  891.00000  1.11%   6.7   55s Explored 177443 nodes (1164346 simplex iterations) in 56.54 seconds Thread count was 1 (of 8 available processors) Optimal solution found (tolerance 0.00e+00) Best objective 9.010000000000e+02, best bound 9.010000000000e+02, gap 0.0% MIP status(2): Model was solved to optimality (subject to tolerances).

Now solve the same model with the same solver on the same machine using 4 threads:

Optimize a model with 177 rows, 549 columns and 3800 nonzeros Presolve time: 0.02s Presolved: 177 rows, 549 columns, 3944 nonzeros Variable types: 1 continuous, 548 integer (496 binary) Found heuristic solution: objective 949.0000000 Root relaxation: objective 4.990000e+02, 947 iterations, 0.03 seconds     Nodes    |    Current Node    |     Objective Bounds      |     Work Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time      0     0  499.00000    0   63  949.00000  499.00000  47.4%     -    0s      0     0  499.00000    0   93  949.00000  499.00000  47.4%     -    0s      0     0  499.00000    0   63  949.00000  499.00000  47.4%     -    0s      0     3  499.00000    0   63  949.00000  499.00000  47.4%     -    0s *  141    97              50     901.0000000  499.00000  44.6%  50.9    0s   6876  3503     cutoff   64       901.00000  558.96236  38.0%  30.4    5s  31149  7878 infeasible   58       901.00000  891.00000  1.11%  18.1   10s  72874  4957     cutoff   63       901.00000  891.00000  1.11%  12.2   18s  87864  4665  891.00000   55    8  901.00000  891.00000  1.11%  11.3   20s . . . . 97009933 49020  897.00000   80   47  901.00000  897.00000  0.44%   5.8 9085s 97054184 47405 infeasible   86       901.00000  897.00000  0.44%   5.8 9090s 97103347 45433 infeasible   95       901.00000  897.00000  0.44%   5.8 9095s 97174397    76 infeasible   97       901.00000  900.91810  0.01%   5.8 9100s Explored 97174474 nodes (560614904 simplex iterations) in 9100.06 seconds Thread count was 4 (of 8 available processors) Optimal solution found (tolerance 0.00e+00) Best objective 9.010000000000e+02, best bound 9.010000000000e+02, gap 0.0% MIP status(2): Model was solved to optimality (subject to tolerances).

Solution times go from 1 minute to 2.5 hours! Extrapolating this to 8 cores gives me the shivers….

Data errors

Even small tables can contain errors. An example data set in a published paper about scheduling maintenance of power generators looks like:

In GAMS I transcribed this as:

table data(i,*)            capacity   allowed-from  allowed-to  outage-weeks *             MW        week           week    number of weeks   unit1      555          1             26           7   unit2      555         27             52           5   unit3      180          1             26           2   unit4      180          1             26           1   unit5      640         27             52           5   unit6      640          1             26           3   unit7      640          1             26           3   unit8      555         27             52           6   unit9      276          1             26          10   unit10     140          1             26           4   unit11      90          1             26           1   unit12      76         27             52           3   unit13      76          1             26           2   unit14      94          1             26           4   unit15      39          1             26           2   unit16     188          1             26           2   unit17      58         27             52           1   unit18      48         27             52           2   unit19     137         27             52           1   unit20     469         27             52           4   unit21      52          1             26           3 ; table manpower(i,t) 'Manpower required for each week'         week1 week2 week3 week4 week5 week6 week7 week8 week9 week10 unit1    10    10     5     5     5     5     3 unit2    10    10    10     5     5 unit3    15    15 unit4    20 unit5    10    10    10    10    10 unit6    15    15    15 unit7    15    15    15 unit8    10    10    10     5     5     5 unit9     3     2     2     2     2     2     2     2     2     3 unit10   10    10     5     5 unit11   20 unit12   10     1     5    15 unit13   15    15 unit14   10    10    10    10 unit15   15    15 unit16   15    15 unit17   20 unit18   15    15 unit19   15 unit20   10    10    10    10 unit21   10    10    10 ;

Just to be sure I added some checks:

set error(i,t) 'check for mismatch between manpower and outage-weeks'; error(i,t)$(manpower(i,t)=0 and ord(t)<=data(i,'outage-weeks')) = yes; error(i,t)$(manpower(i,t)<>0 and ord(t)>data(i,'outage-weeks')) = yes; abort$card(error) "manpower mismatch",error;

Low and behold, we see:

----     93 manpower mismatch ----     93 SET error  check for mismatch between manpower and outage-weeks              week4 unit12         YES **** Exec Error at line 93: Execution halted: abort$1 'manpower mismatch'

Indeed we have for this unit a problem in the manpower allocation.

Intel

For parallel MIP the GPU based solutions such as http://www.nvidia.com/object/tesla-supercomputing-solutions.html are not very useful (although for some specialized applications GPU based optimization algorithms have been developed). Now Intel has an alternative:

http://www.drdobbs.com/parallel/intels-50-core-xeon-phi-the-new-era-of-i/240105810
http://www.intel.com/content/www/us/en/processors/xeon/xeon-phi-detail.html

The 60 cores sound attractive, but the limited amount of memory (8GB) may be a problem for big MIPs.

Gurobi integer feasibility tolerance

The integer feasibility tolerance determines when a fractional variable can be considered “automatically” integer during the branch-and-bound search. Gurobi allows this to be set as tight as 1.0e-9 (option IntFeasTol). But a client gets the following:

> I still get binary variables like 0.000008 instead of 0.

I actually believe this is a valid question. This is about 1.0e-6. Unfortunately the answer from Gurobi support is somewhat dismissive:

> This is a natural consequence of integer programming, which solves models via a series of linear programs.  See FAQ 23:
http://www.gurobi.com/resources/faqs

Scaling can have notorious impact on LP feasibility tolerances (e.g. the scaled model can solve to optimality, but after unscaling become very infeasible). The LP feasibility tolerance controls how much a variable can be outside its bounds before becoming infeasible (or how much an equation can be violated before becoming infeasible – this is just how much a slack can be outside its bounds). I don’t think scaling has an effect on the integer feasibility tolerance.

Note that Cplex allows a integer feasibility tolerance of zero (parameter epint). At first this seems crazy, but actually works fine in models where we need variables to be really discrete. I guess Cplex may just need to do more work in this case: we may need to branch further when a binary variable that is still fractional assumes a value of 1.0e-9.

PS: See the comments for some interesting feedback. The real question remains: why if we request an integer feasibility tolerance of 1e-9 we observe fractional parts of 1e-6.