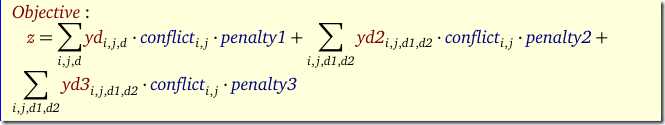In this post a question was asked about a small interesting scheduling problem. The model was implemented in C++ using Cplex. Debugging someone else’s C++ code is not my favorite pastime so instead just lets implement the model in a modeling language (that also is probably faster than staring at some C++ code).
We have 10 time slots (two per day). We want to assign 59 different exams to time slots such that students that do multiple exams are not burdened more than needed. We have some data indicating conflicts: for exam pairs \((i,j)\) (with \(i<j\)) we have the number of students that want to take both exams. This number is called \(\mathit{conflicts}_{i,j}\).

This matrix is strictly upper-triangular. In the above picture there are some apparent sub-diagonal elements but that is a visual aberration. This is the result from dropping rows and columns without entries. The central binary variable is:
\[x_{i,t} = \begin{cases} 1 & \text{if exam $i$ is taken at period $t$} \\
0 & \text{otherwise}
\end{cases}\] |
The hard constraints are as follows: each exam is offered exactly one time, and exams with conflicts cannot be offered at the same time. These are the easy ones:

The soft constraints are:
- A penalty of 6 for each student that has two exams on one day.
- A penalty of 1 for each student with exams on two consecutive days.
- A penalty of 2 for each student with an afternoon exam followed by morning exam the next day.
All these penalties are based on a similar concept: count the conflicts. This counting is done as follows:

Here the variables yd, yd2 and yd3 are binary variables (although they can be relaxed to continuous variables between zero and one). We can just use a lower bound as we are minimizing those counts. The sets dt1, dt2 and dt3 indicate the periods to consider. E.g. dt1 looks like:

dt2 is:

dt3 is a subset of dt2:

The objective is to minimize the penalties on the conflicts:
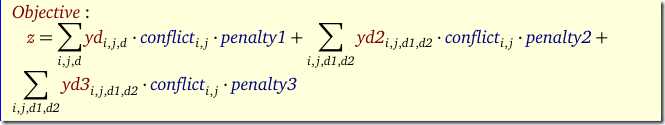
The final model solves quite reasonably with Cplex:

Here the blue line is the objective (best found) and the red line is the lower bound (best possible). We see that Cplex finds good solutions quickly but needs more time to prove optimality. To get good performance I helped Cplex a little bit with setting branching priorities and using some options suggested by a tuning run.
Note: the plot was produced by the GAMS/Cplex option miptrace and some R code:
> ggplot(data=exam,aes(x=seconds))+geom_line(aes(y=bestFound),color="blue",size=1.1)+
+ geom_line(aes(y=(bestBound)),color="red")+ylim(0,500)+ylab("objective")
The results look like:

Here, we allocated penalties for a conflict \((i,j)\) to \(i\). Note that it would be easy to add a capacity constraint where we would limit the number of parallel exams in each time period. The would prevent the uneven distribution of exams over the time periods.
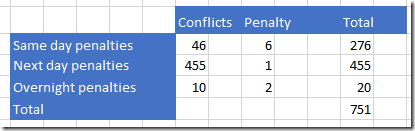
The conflicts are numerous. We have 14 same day conflicts;

The solution has further a lot of next day conflicts (although it is able to circumvent the ones with a really high student count).
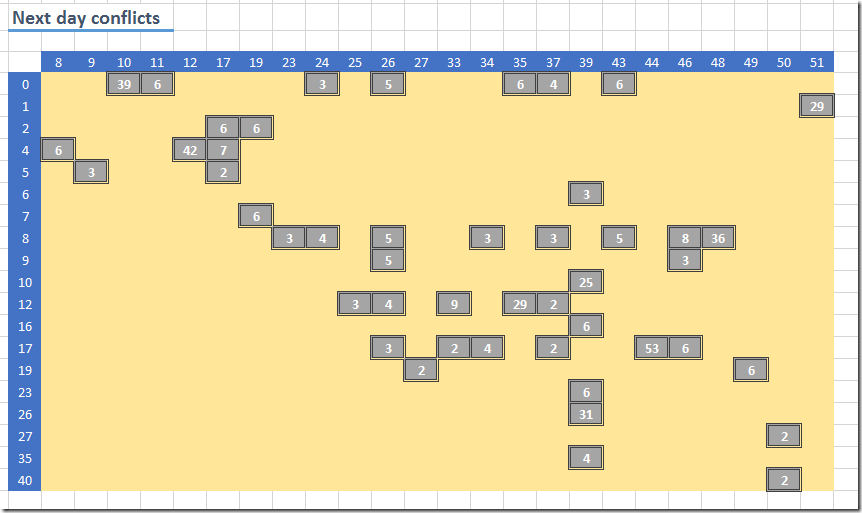
There are just a few overnight conflicts:

Note that these come in addition to the next day conflicts. The total of these (where we apply given penalties) result in our optimal objective:
In my opinion it is much more convenient to develop models in a modeling language as this will allow you to think and reason better about the model equations and to make quick changes to the model. Once that is working you can always translate these constructs into C++ or other programming languages.