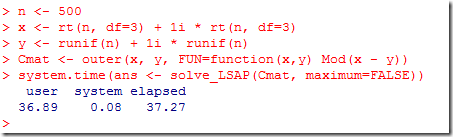
In http://thread.gmane.org/gmane.comp.lang.r.general/169477/focus=169690 an assignment problem is formed and solved with the Hungarian method in R:
Current LP solvers are very fast: when we solve this with Gurobi we see:
Presolve time: 0.34 sec.
Iteration Objective Primal Inf. Dual Inf. Time
0 0.0000000e+00 1.000000e+03 0.000000e+00 0s
8329 7.4610203e+02 3.115000e+03 0.000000e+00 5s
11696 7.5580772e+02 0.000000e+00 0.000000e+00 9sSolved in 11696 iterations and 9.30 seconds
I.e. about three times as fast. So not just any specialized algorithm can beat an excellent general purpose LP solver at all times.
Note: for n=1000 the timings for R are:
Solved in 40291 iterations and 141.13 seconds

Dual simplex as I assume GuRoBi use is usually quite fast. The specialized network flow optimizer in MOSEK (or in CPLEX) may be even faster.
ReplyDeleteErling
If a GAMS program with your problem is available somewhere then let me know.
ReplyDeleteErling
No doubt a better engineered network code will improve this by a large margin (e.g. Cplex network algorithm solves these models in 0.25 and 1.58 seconds). Then we are comparing network codes. However, the point I wanted to make, somewhat inarticulate no doubt, was that a standard lp solver does not always have to be slow compared to specialized solvers. Anyway, the problems are in GAMS, and can be retrieved from http://amsterdamoptimization.com/models/assignmentR.zip.
ReplyDeleteErwin makes a good point. Sparse LP solvers are so fast that they are competitive with the performance of many special-purpose solvers. Furthermore, many problems with special structure - such as network models - have side constraints. And once you consider side constraints, you're usually better off with a general purpose solver.
ReplyDeleteI totally agree with both dual simplex is surprisingly fast. That was also the intended implication of my initial post.
ReplyDeleteIt is amazing it can compete with a specialized network simplex solver.
Just a quick note. We downloaded your GAMS model. Thanks. MOSEK has a mode where it detect the embedded network structure.
ReplyDeleteBut GAMS or at least the GAMS/MOSEK link puts the objective in the constraints because in GAMS you do
min z
st c'x = z
...
so we should change MOSEK so it take that into account.
Sorry, my last put should say if the objective is in the constraints then the problem does not have network structure and hence we will detect the embedded network structure.
ReplyDeleteSo your examplepoint out a problem in the GAMS/MOSEK link.
GAMS has an objective variable instead of an objective function. If the objvar appears only once (linearly) in the model, and has no bounds, it can be substituted out. Most links do that automatically so the solver sees a proper objective function. This is especially important for nonlinear solvers.
ReplyDeleteThese reformulations are explained in the documentation for the GAMS IO library. You may want to ask GAMS for a copy.
ReplyDeleteI think GAMS has new link structure. As far as I understand our link should be rewritten soon and that will solve this problem.
ReplyDeleteBtw the specialized network flow alg in MOSEK does much better than dual simplex on your assignment problem. We will most likely provide Mittleman with a few cases. They will be good for his network solver test.