- Let \(I = \{1,\dots,n\}\)
- We have two parameters \(a_i, b_i \ge 0\)
- Find a subset \(S\subset I\) that maximizes the following expression \[\max \left(\sum_{i \in S} a_i\right) \left(\sum_{i \notin S} b_i\right) \]
This is easily formulated as a Mixed Integer Quadratic Programming (MIQP) problem. We can write:
| MIQP Model |
|---|
| \[\begin{align}\max &\left(\sum_i a_i x_i \right) \left(\sum_i b_i (1-x_i) \right) \\ & x_i \in \{0,1\}\end{align}\] |
Using a modeling system like GAMS we can directly implement this:
obj.. z =e= sum(i, a(i)*x(i)) * sum(i, b(i)*(1-x(i)));
It is interesting to see what different solvers do with this. The model can be reformulated by the solver in different ways, so we can potentially see very different behavior. I generated some random values (uniformly distributed) for the parameters: \[\begin{align} &n=100\\ & a_i \sim U(0,1)\\ & b_i \sim U(0,1)\end{align}\] This is already large enough to make it interesting. Complete enumeration is out of the question: \[2^{100} = 1267650600228229401496703205376\] The generated input data looks like:
---- 7 PARAMETER a i1 0.172, i2 0.843, i3 0.550, i4 0.301, i5 0.292, i6 0.224, i7 0.350, i8 0.856 i9 0.067, i10 0.500, i11 0.998, i12 0.579, i13 0.991, i14 0.762, i15 0.131, i16 0.640 i17 0.160, i18 0.250, i19 0.669, i20 0.435, i21 0.360, i22 0.351, i23 0.131, i24 0.150 i25 0.589, i26 0.831, i27 0.231, i28 0.666, i29 0.776, i30 0.304, i31 0.110, i32 0.502 i33 0.160, i34 0.872, i35 0.265, i36 0.286, i37 0.594, i38 0.723, i39 0.628, i40 0.464 i41 0.413, i42 0.118, i43 0.314, i44 0.047, i45 0.339, i46 0.182, i47 0.646, i48 0.561 i49 0.770, i50 0.298, i51 0.661, i52 0.756, i53 0.627, i54 0.284, i55 0.086, i56 0.103 i57 0.641, i58 0.545, i59 0.032, i60 0.792, i61 0.073, i62 0.176, i63 0.526, i64 0.750 i65 0.178, i66 0.034, i67 0.585, i68 0.621, i69 0.389, i70 0.359, i71 0.243, i72 0.246 i73 0.131, i74 0.933, i75 0.380, i76 0.783, i77 0.300, i78 0.125, i79 0.749, i80 0.069 i81 0.202, i82 0.005, i83 0.270, i84 0.500, i85 0.151, i86 0.174, i87 0.331, i88 0.317 i89 0.322, i90 0.964, i91 0.994, i92 0.370, i93 0.373, i94 0.772, i95 0.397, i96 0.913 i97 0.120, i98 0.735, i99 0.055, i100 0.576 ---- 7 PARAMETER b i1 0.051, i2 0.006, i3 0.401, i4 0.520, i5 0.629, i6 0.226, i7 0.396, i8 0.276 i9 0.152, i10 0.936, i11 0.423, i12 0.135, i13 0.386, i14 0.375, i15 0.268, i16 0.948 i17 0.189, i18 0.298, i19 0.075, i20 0.401, i21 0.102, i22 0.384, i23 0.324, i24 0.192 i25 0.112, i26 0.597, i27 0.511, i28 0.045, i29 0.783, i30 0.946, i31 0.596, i32 0.607 i33 0.363, i34 0.594, i35 0.680, i36 0.507, i37 0.159, i38 0.657, i39 0.524, i40 0.124 i41 0.987, i42 0.228, i43 0.676, i44 0.777, i45 0.932, i46 0.201, i47 0.297, i48 0.197 i49 0.246, i50 0.646, i51 0.735, i52 0.085, i53 0.150, i54 0.434, i55 0.187, i56 0.693 i57 0.763, i58 0.155, i59 0.389, i60 0.695, i61 0.846, i62 0.613, i63 0.976, i64 0.027 i65 0.187, i66 0.087, i67 0.540, i68 0.127, i69 0.734, i70 0.113, i71 0.488, i72 0.796 i73 0.492, i74 0.534, i75 0.011, i76 0.544, i77 0.451, i78 0.975, i79 0.184, i80 0.164 i81 0.025, i82 0.178, i83 0.061, i84 0.017, i85 0.836, i86 0.602, i87 0.027, i88 0.196 i89 0.951, i90 0.336, i91 0.594, i92 0.259, i93 0.641, i94 0.155, i95 0.460, i96 0.393 i97 0.805, i98 0.541, i99 0.391, i100 0.558
MIQP Solvers: Cplex, Gurobi and Baron
Cplex solves this very fast, all in the root node:
Nodes
Cuts/
Node Left
Objective IInf Best Integer Best Bound ItCnt
Gap
* 0+ 0 0.0000 1807.5989 ---
Found incumbent of value 0.000000 after 0.89 sec.
(112.24 ticks)
* 0+ 0 874.9563 1807.5989 106.59%
Found incumbent of value 874.956296 after 0.89 sec.
(112.41 ticks)
0 0
903.7995 100 874.9563 903.7995 3357
3.30%
0 0
896.6965 182 874.9563 Cuts: 1268 3752
0.00%
0 0
889.7657 772 874.9563 Cuts: 1337 4088
0.00%
0 0
882.7062 1112 874.9563 ZeroHalf: 1337 4432
0.00%
0 0
877.9208 2106
874.9563 ZeroHalf: 1337
4827 0.00%
0 0
875.4173 762 874.9563 ZeroHalf: 1098 5071
0.00%
0 0
cutoff 874.9563 5112 ---
Elapsed time = 10.70 sec. (3363.84 ticks, tree = 0.01
MB, solutions = 2)
|
The solution looks like:
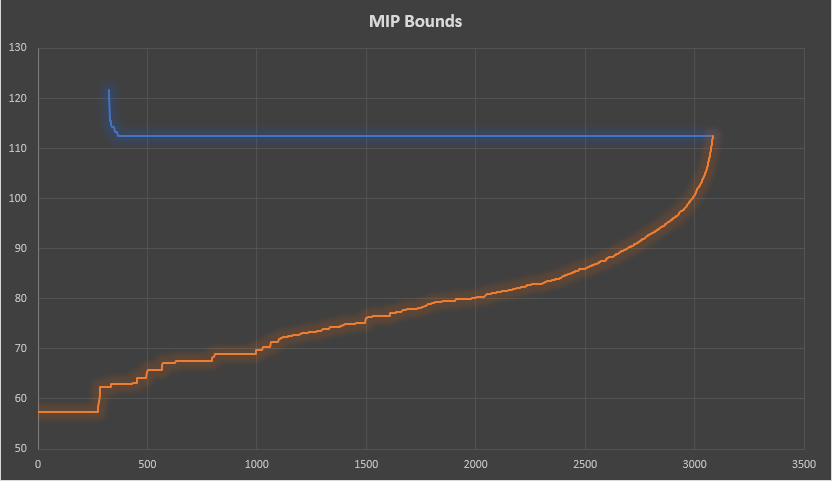
Gurobi has some real troubles with this model. After 10,000 seconds I stopped it:
---- 21 VARIABLE x.L selection (binary) i1 1.000, i2 1.000, i3 1.000, i8 1.000, i11 1.000, i12 1.000, i13 1.000, i14 1.000 i19 1.000, i20 1.000, i21 1.000, i25 1.000, i26 1.000, i28 1.000, i34 1.000, i37 1.000 i38 1.000, i39 1.000, i40 1.000, i47 1.000, i48 1.000, i49 1.000, i52 1.000, i53 1.000 i58 1.000, i60 1.000, i64 1.000, i67 1.000, i68 1.000, i70 1.000, i74 1.000, i75 1.000 i76 1.000, i79 1.000, i81 1.000, i83 1.000, i84 1.000, i87 1.000, i88 1.000, i90 1.000 i91 1.000, i92 1.000, i94 1.000, i96 1.000, i98 1.000, i100 1.000 ---- 21 PARAMETER count = 46.000 number of x(i)=1 VARIABLE z.L = 874.956 objective variable
Gurobi has some real troubles with this model. After 10,000 seconds I stopped it:
Nodes
| Current Node |
Objective Bounds | Work
Expl Unexpl | Obj
Depth IntInf | Incumbent
BestBd Gap | It/Node Time
0
0 1028.82147 0 88
-0.00000 1028.82147 - -
0s
H 0
0
94.1937601 1028.82147
992% - 0s
H 0
0
874.9562964 1028.82147
17.6% - 0s
0
2 1028.82147 0 88
874.95630 1028.82147 17.6% -
0s
5024
3355 981.36042 24
77 874.95630 989.02791
13.0% 2.4 5s
H13738 10488 874.9564248 978.66510
11.9% 2.4 8s
20782 16103
909.88622 55 44
874.95642 975.04173 11.4%
2.4 10s
43494 34084
943.11968 43 57
874.95642 968.63227 10.7%
2.4 15s
65078 50966
916.66669 49 50
874.95642 964.88315 10.3%
2.4 20s
89405 69894
904.98150 56 44
874.95642 962.21433 10.0%
2.4 25s
114800 89612
898.26415 51 50
874.95642 959.84933 9.70%
2.4 30s
136964 106525 911.88894
51 49 874.95642
958.31653 9.53% 2.4
35s
162025 125584 892.69915
52 48 874.95642
956.85312 9.36% 2.4
40s
184525 142823 922.61714
44 57 874.95642
955.79186 9.24% 2.4
45s
208972 161530 880.72495
54 46 874.95642
954.67328 9.11% 2.4
50s
231067 178124 885.81556
57 44 874.95642
953.79519 9.01% 2.4
55s
255408 196541 935.18869
46 54 874.95642
952.89911 8.91% 2.4
60s
278680 214033 899.07410
51 47 874.95642
952.12450 8.82% 2.4
65s
302859 232220 936.52130
37 64 874.95642
951.40827 8.74% 2.4
70s
328028 251086 910.60834
50 50 874.95642
950.70076 8.66% 2.4
75s
352051 268955 905.74964
54 45 874.95642
950.10317 8.59% 2.4
80s
376120 286723 902.67637
57 43 874.95642
949.57421 8.53% 2.4
85s
400406 304716 949.03348
26 77 874.95642
949.03348 8.47% 2.4
90s
422676 321239 882.35938
52 47 874.95642
948.53308 8.41% 2.4
95s
. . .
13091984 8119359 883.24548
54 44 874.95642
919.65956 5.11% 2.4 9990s
13094401 8120718 cutoff
55 874.95642 919.65790
5.11% 2.4 9995s
13095972 8121550 897.09522
56 41 874.95642
919.65687 5.11% 2.4 10000s
13098502 8122984 908.84424
50 50 874.95642
919.65560 5.11% 2.4 10005s
13100870 8124293 874.95653
56 44 874.95642
919.65388 5.11% 2.4 10010s
13103160 8125658 883.98954
56 46 874.95642
919.65273 5.11% 2.4 10015s
13105665 8127116 889.74823
60 40 874.95642
919.65125 5.11% 2.4 10020s
13107878 8128361 cutoff
61 874.95642 919.64989
5.11% 2.4 10025s
13110794 8129992 880.12914
53 48 874.95642
919.64814 5.11% 2.4 10030s
13112818 8131096 891.49116
58 43 874.95642
919.64674 5.11% 2.4 10035s
Sending CtrlC
signal
Explored 13114854
nodes (31784166 simplex iterations) in 10037.84 seconds
Thread count was 4
(of 8 available processors)
Solution count 4:
874.956 874.956 94.1938 -0
Solve interrupted
Best objective
8.749562757165e+02, best bound 9.196456216128e+02, gap 5.1076%
MIQP status(11):
Optimization was terminated by the user.
|
Gurobi finds the optimal solution quickly but it is not able to prove optimality.
Interestingly, the global solver Baron does a very good jobs on this:
Preprocessing
found feasible solution with value
0.00000000000
Doing local search
Preprocessing found feasible solution with
value 874.943601492
Solving bounding LP
Starting multi-start local search
Preprocessing found feasible solution with
value 874.956296356
Done with local search
===========================================================================
Iteration
Open nodes Time (s) Lower bound Upper bound
1 0 1.00 874.956 874.956
Cleaning up
*** Normal
completion ***
Wall clock time: 1.00
Total CPU time used: 0.75
|
Linearization
Let's see if we can make Gurobi look a little bit better. We can reformulate the model as a straight mixed-integer programming model:
| MIP Model |
|---|
| \[\begin{align} \max & \sum_{i \ne j} a_i b_j y_{i,j} \\ & y_{i,j} \le x_i && \forall i \ne j \\ & y_{i,j} \le 1-x_j && \forall i \ne j \\ & 0 \le y_{i,j} \le 1 \\ & x_i \in \{0,1\} \end{align}\] |
This model introduces \(100 \times 100 - 100 = 9,900\) extra continuous variables (and 19,800 additional constraints).
Derivation
We can rewrite \[\max \left(\sum_i a_i x_i \right) \left(\sum_i b_i (1-x_i) \right) \] as \[\max \sum_{i,j} a_i b_j x_i (1-x_j) \] We can linearize the product \[y_{i,j} = x_i (1-x_j)\] as \[\begin{align} & y_{i,j} \le x_i \\ & y_{i,j} \le (1-x_j) \\ & y_{i,j} \ge x_i - x_j \\ & y_{i,j}, x_i \in \{0,1\}\end{align}\] You can verify the correctness of this by plugging in the possible values for \((x_i,x_j) = \{(0,0),(0,1),(1,0),(1,1)\}\). Finally we observe:
- \(y_{i,j}\) can be relaxed to be continuous between 0 and 1. It will be integer automatically.
- We are really maximizing \(y_{i,j}\) so we can drop the last \(\ge\) constraints.
- We can skip the case where \(i=j\): the product \(x_i (1-x_i)\) is always zero.
This formulation proves to be quite beneficial for Gurobi:
Nodes
| Current Node |
Objective Bounds | Work
Expl Unexpl | Obj
Depth IntInf | Incumbent BestBd
Gap | It/Node Time
0
0 903.79947 0
100 -0.00000 903.79947 -
- 2s
H 0
0
2.2104609 903.79947 -
- 3s
H 0
0
163.3432337 903.79947 453%
- 3s
H 0
0
177.4409096 903.79947 409%
- 3s
H 0
0
672.0256560 903.79947 34.5%
- 3s
H 0
0
690.8350810 903.79947 30.8%
- 3s
0
0 903.64085 0
100 690.83508 903.64085
30.8% - 3s
H 0
0
787.7021585 903.64085 14.7%
- 3s
0
0 903.47324 0
100 787.70216 903.47324
14.7% - 4s
0
0 903.30963 0
100 787.70216 903.30963
14.7% - 4s
0
2 903.30963 0
100 787.70216 903.30963
14.7% - 7s
* 4
4 2 874.9562964 888.63188
1.56% 737 9s
Cutting planes:
Gomory: 9
Explored 7 nodes
(16549 simplex iterations) in 9.53 seconds
Thread count was 4
(of 8 available processors)
Solution count 8:
874.956 787.702 690.835 ... -0
Optimal solution
found (tolerance 0.00e+00)
Best objective
8.749562963561e+02, best bound 8.749562963561e+02, gap 0.0000%
MIP status(2):
Model was solved to optimality (subject to tolerances).
|
Instead of doing this linearization by ourselves, we can also tell Gurobi to do this by using the option preqlinearize. (The behavior is not exactly the same, it solved in 12 seconds instead of 9). The automatic behavior is apparently not to apply the linearization. Too bad Gurobi does not realize it is in so much trouble and should reformulate the problem.
We can predict the optimal solution for our specific random data set quite easily:
Of course, this approach will only work for certain very "balanced" data sets. We exploited here that \(a_i\) and \(b_i\) are drawn from the same distribution. In addition, we have no cases where \(a_i=b_i\). I don't know about good heuristics for the more general case.
A related problem (or better: a special case) only looks at parameter \(a\):\[\max \left(\sum_{i \in S} a_i\right) \left(\sum_{i \notin S} a_i\right) \] This problem, as noted in the comments below, has an interesting linearization. The MIQP formulation is again straightforward: \[\begin{align}\max & \left(\sum_i a_i x_i \right) \left(\sum_i a_i (1-x_i) \right)\\ & x_i \in \{0,1\}\end{align} \] We can find the optimal solution by solving instead \[\min \left|\sum_i a_i x_i - \sum_i a_i (1-x_i) \right| \] I.e. make sure we divide into \(I\) into \(S\) and \(I-S\) as evenly as possible. The absolute value is easily linearized, yielding a MIP model.
Note that when we write \(A=\sum_i a_i\), we can state this as: \[\min \left| \sum_i a_i x_i - \frac{A}{2}\right|\]
Here are some performance figures for this problem:
So we see:
Cheating: a simple heuristic
We can predict the optimal solution for our specific random data set quite easily:
- if \(a_i\gt b_i\), set \(x_i=1\)
- if \(a_i\lt b_i\), set \(x_i=0\)
This correctly shows the optimal solution:
---- 18 heuristic solution ---- 18 VARIABLE x.L selection (binary) i1 1.000, i2 1.000, i3 1.000, i8 1.000, i11 1.000, i12 1.000, i13 1.000, i14 1.000 i19 1.000, i20 1.000, i21 1.000, i25 1.000, i26 1.000, i28 1.000, i34 1.000, i37 1.000 i38 1.000, i39 1.000, i40 1.000, i47 1.000, i48 1.000, i49 1.000, i52 1.000, i53 1.000 i58 1.000, i60 1.000, i64 1.000, i67 1.000, i68 1.000, i70 1.000, i74 1.000, i75 1.000 i76 1.000, i79 1.000, i81 1.000, i83 1.000, i84 1.000, i87 1.000, i88 1.000, i90 1.000 i91 1.000, i92 1.000, i94 1.000, i96 1.000, i98 1.000, i100 1.000 ---- 18 PARAMETER count = 46.000 number of x(i)=1 EQUATION obj.L = 874.956
Of course, this approach will only work for certain very "balanced" data sets. We exploited here that \(a_i\) and \(b_i\) are drawn from the same distribution. In addition, we have no cases where \(a_i=b_i\). I don't know about good heuristics for the more general case.
A related problem
A related problem (or better: a special case) only looks at parameter \(a\):\[\max \left(\sum_{i \in S} a_i\right) \left(\sum_{i \notin S} a_i\right) \] This problem, as noted in the comments below, has an interesting linearization. The MIQP formulation is again straightforward: \[\begin{align}\max & \left(\sum_i a_i x_i \right) \left(\sum_i a_i (1-x_i) \right)\\ & x_i \in \{0,1\}\end{align} \] We can find the optimal solution by solving instead \[\min \left|\sum_i a_i x_i - \sum_i a_i (1-x_i) \right| \] I.e. make sure we divide into \(I\) into \(S\) and \(I-S\) as evenly as possible. The absolute value is easily linearized, yielding a MIP model.
Note that when we write \(A=\sum_i a_i\), we can state this as: \[\min \left| \sum_i a_i x_i - \frac{A}{2}\right|\]
Here are some performance figures for this problem:
| Solver | Model | Time | Obj | Gap |
|---|---|---|---|---|
| Cplex | MIQP | >3600 | 465.931 | 40% |
| Gurobi | MIQP | >3600 | 465.931 | 65% |
| Baron | MIQP | 2 | 465.931 | Optimal |
| Cplex | MIP | 4 | 465.931 | Optimal |
| Gurobi | MIP | 1 | 465.931 | Optimal |
So we see:
- Cplex and Gurobi do not like the MIQP model at all. They stopped on a time limit before optimality was proven. This is worse performance than on the original problem with both \(a\) and \(b\).
- Baron does a really good job. Baron is a global NLP/MINLP solver, so it is somewhat surprising to me that it is doing so much better than more specialized MIQP solvers.
- The MIP formulations are easy to solve.
- The objective reported for the MIP models is not the MIP objective but rather \(\left(\sum_i a_i x_i \right) \left(\sum_i a_i (1-x_i) \right)\) evaluated at the solution point.
The Baron log is just very convincing:
Iteration
Open nodes Time (s) Lower bound Upper bound
* 1 1 2.00 465.931 1863.72
1 0 2.00
465.931 465.931
|
Conclusion
MIQP models, including rather smallish ones, remain very difficult to solve, even with expensive commercial solvers. The only solver that is consistently doing a good job is Baron. For most solvers it pays off to look for linearizations.
References
- Maximize the product of the sum of two subsets, https://cs.stackexchange.com/questions/71168/maximize-product-of-sum-of-two-subset