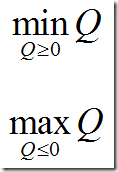Calculating the Bacon number: a shortest path network

The Bacon number measures how far an actor is removed from Kevin Bacon in terms of playing in the same movie. I received a data set with actors and movies. As this problem can be written as standard network model we can easily solve this with an LP solver.

Networks are often an important part of math programming models. We see them in supply chain models, in models dealing with electricity grids, regional trade flows, transportation etc. Not all users find this easy to model. Here some notes:

• In this model we moved some of the complexity into the data manipulation step. As a result the equations are very simple. Complex equations are much more difficult to debug.
• The sparse vector b only has two elements. In GAMS only the non-zero elements are stored so this is quite efficient.
• Sometimes users use three different type of flow balance equations. I prefer a single equation block with source and sink modeled via this b vector.
• I have seen implementations where movies are also part of the network. In this case I only have “actor-nodes”, which makes the network smaller.
• The set arcs plays an important role in the topology of the network.
• The network is sparse: many arcs do not exist. This is beneficial for the LP solver.
• I sometimes see users creating a large cost to indicate a link can not be chosen. I think it is often much better to exclude such links from the set arcs.
• In this case we have modeled a directed graph. I prefer to use directed links as the results are easier to interpret and the modeling is much more straightforward. When using undirected arcs we need to look at the sign of the flows. 
• The Bacon number is the length of the shortest path where each link has a unit length. Not each optimal solution is unique. This is a pure network model; in practice we often see more complex models with a network component.
• For pure networks we can easily form and solve the dual. I prefer to stay closer to the problem with a more intuitive primal formulation.
• Of course Google can find these numbers for you:
  

monotonic transformations

From: lp_solve@yahoogroups.com
To: lp_solve@yahoogroups.com
Date: Thu, 9 Jul 2015 00:32:47 -0700
Subject: [lp_solve] C# to set the object with the form of square

Could LP set the object in a form of square? Just like this :
min: Q^2

If we have Q≥0 then just use MIN Q. We can apply a monotonic function. I have used this trick a lot in the context of minimizing distances. Instead of

we can keep things quadratic by using

This got rid of a nasty square root and this allowed us use quadratic solvers.

Back to the original problem where we want to remove a square. What if we don’t know in advance that Q≥0? Then we can solve two problems:

and pick the best one.

The suggested solution in the thread: “Have a look into piecewise linear approximations” is at least much overkill.

Accessing GAMS GDX files as database tables

GAMS GDX files are accessed via an a low-level API. One way to make GDX files more appealing to programmers is to use a higher-level API. One possibility is to use an SQL API. This allows us to use  a very familiar API, Also we can apply certain transformations directly at the SQL level to make data more useful for the host application. Note that we don’t import GDX data into a database here, but rather access GDX data directly through an SQL engine.

GAMS data can often be mapped to SQL tables in a straightforward manner:

Interestingly, we have used SQLite and their virtual table mechanism (https://www.sqlite.org/vtab.html) for this exercise. SQLite allows to store strings in any column. In that sense it is more like Excel. This flexible mechanism would allow us to store normal numbers as DOUBLE values and those GAMS related special values as TEXT.

Here is a small example:

Results from prototype implementation:

Note that the GAMS code to get this result is more complicated:

Sorting is another area where SQL is much more convenient than GAMS code. Being able to do things where GAMS lacks expressiveness seems like a win to me.

With this SQL layer there are many new possibilities, such as:

• Use GDX files through ODBC allowing many applications to access GDX data without any programming effort
• The same ODBC layer also allows access to GDX data from many programming languages using a standard, well-known API
• Use GDX files through LINQ queries from .Net applications
• Writing GDX files (but there are severe restrictions in the GDX API in this respect – e.g. one symbol at the time and only one batch of inserts, no updates).

Of course the price we pay is performance. In many cases we need to do a full table scan. For extremely large data sets, programming directly against the GDX API is still the best solution. Note that in some cases we can increase performance by importing data into a local data base using a SELECT … INTO, after which we can add some clever SQL indices.  

Multinomial probability derivation

For an optimization problem related to media planning I needed to evaluate the probability that a multinomial variate assume the value zero. This can be written as:

However it was suggested to use the following expression:

I did not see immediately that these things are approximately the same. With a little bit of effort:

where the last step is based on a Taylor approximation:

To be precise:

This approximation in evaluating the reach for some advertisement plans seem to work very well.