Problem Description
From: http://math.stackexchange.com/questions/1652150/turn-off-the-ovens-an-optimization-problem:
I am not at all sure the physics make sense, but let’s focus on the mathematics of this model.
Formulation A
An MINLP formulation could be:
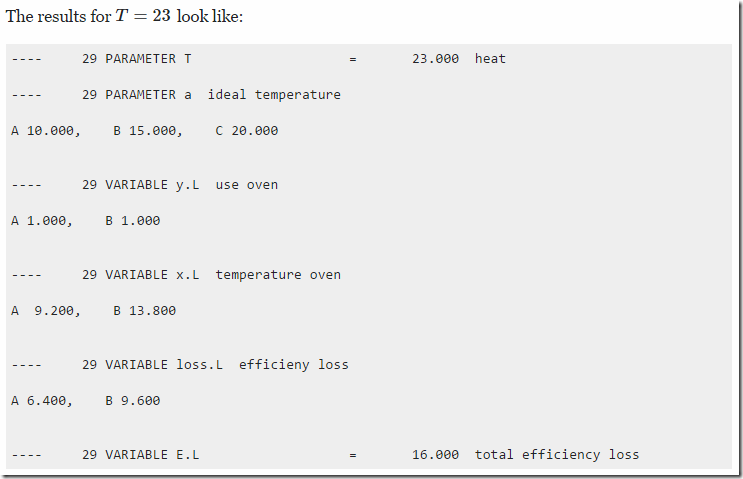
The idea is:
- If \(y_i=0\) (oven is turned off) we force \(x_i=0\) (equation Off). Also we have \(loss_i=0\) as we multiplied the loss function by \(y_i\).
- If \(y_i=1\) (oven is turned on), we let the solver decide on \(x_i\). In almost all cases it will choose a value > 0 as it wants to be somewhat close to \(a_i\). But if \(x_i\) would become zero something special happens: suddenly \(y_i=0\) becomes a better solution.
- We don’t have to model explicitly \(x_i=0 \implies y_i=0\). If \(x_i=0\) then the objective would have a preference for \(y_i=0\) as this will improve the objective.
This model is no longer quadratic. For small instances like this we can use a global solver without a problem.
Formulation B
If we can make the problem quadratic and convex we can solve the problem with many more solvers. So here is a formulation that does just that:
Here we have:
- If \(y_i=0\) (oven is turned off) we force \(x_i=0\) (equation Off). The slack \(s_i\) is left floating. This will cause the algorithm to choose a slack such that the loss is zero.
- If \(y_i=1\) (oven is turned on) we force \(s_i=0\) (equations On1,On2).
As this model is convex all MIQP solvers can handle this.
Conic formulation
For a compact conic formulations of this problem see: http://blog.mosek.com/2016/03/reformulating-non-convex-minlp-as-misocp.html

No comments:
Post a Comment