Spatial Equilibrium

Just a quick experiment with a small price-endogenous spatial equilibrium model.

In this problem, we consider commodities (goods) produced and consumed in different regions. We can trade between regions.

This price-endogenous spatial model will find both equilibrium prices, supplies, demand quantities, and trade patterns. Our model will have a connection with the transportation model. The difference is that we formulate the model as a system of complementarity constraints (no objective), with the duals explicitly in the model as variables. Or, in other words, we solve the KKT conditions.

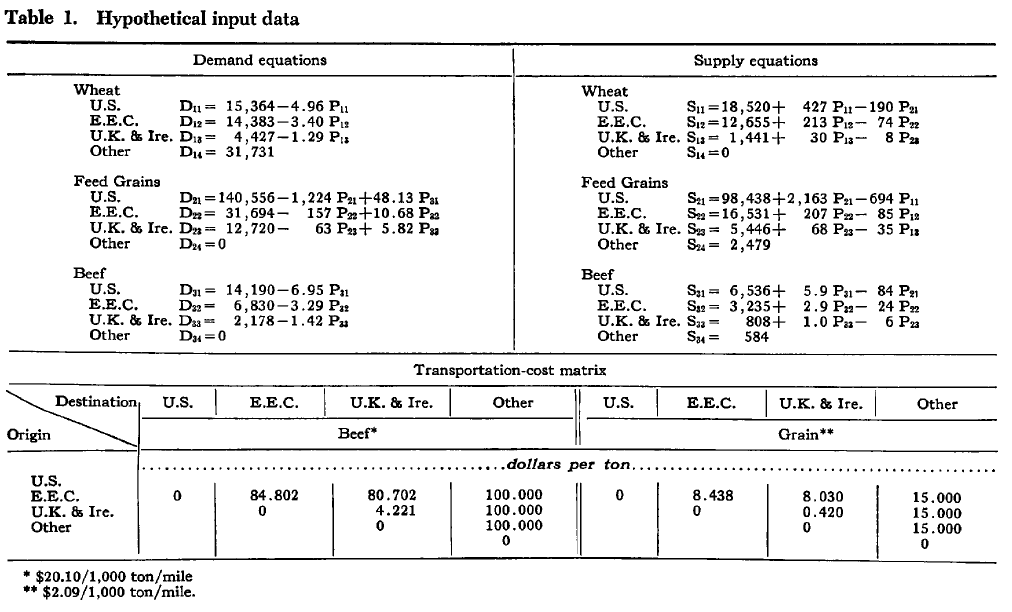
I use a small data set from [3], and see if we can reproduce things.

Demand and supply functions

In the simplest form, we assume we have estimated linear supply and demand curves as follows: \[\begin{align}&\color{darkred}{Q}^{\color{darkred}d}_{c,r} = \color{darkblue}a_{c,r} +   \color{darkblue}b_{c,r}\color{darkred}{P}_{c,r}\\ &\color{darkred}{Q}^{\color{darkred}s}_{c,r} = \color{darkblue}\alpha_{c,r} +   \color{darkblue}\beta_{c,r}\color{darkred}{P}_{c,r}\end{align}\] The means, the demand and supply quantities depend on the price, The indices \(c,r\) indicate the commodity and region. 

Notes:

• Demand/supply functions are typically of the form \(\color{darkred}Q=f(\color{darkred}P)\). Some models use the inverse demand and supply functions: \(\color{darkred}P=f^{-1}(\color{darkred}Q)\). Of course, when solved as a system of equations, this does not make a difference: we can use either form.
• We can assume the demand function is downward sloping (higher prices mean less demand) and the supply function is upward sloping (higher prices mean more supply). Normal goods all follow this. There are only very rare cases where this is not the case. Examples of goods with upward-sloping demand curves are Giffen and Veblen goods [1].
• The demand and supply functions can be a little bit more complicated by also considering the prices of other goods. E.g. the supply of beef may depend on the price of beef but also on the price of feed grains. For the latter, we would expect that if feed prices increase, the supply of beef decreases. We can write in general:\[\begin{align}&\color{darkred}{Q}^{\color{darkred}d}_{c,r} = \color{darkblue}a_{c,r} +   \sum_{c'}\color{darkblue}b_{c,r,c'}\color{darkred}{P}_{c',r}\\ &\color{darkred}{Q}^{\color{darkred}s}_{c,r} = \color{darkblue}\alpha_{c,r} +   \sum_{c'}\color{darkblue}\beta_{c,r,c'}\color{darkred}{P}_{c',r}\end{align}\] This is the form [3] is using.
• A possible way to find values for the coefficients of these functions is to use an econometric analysis (regression). When we don't have enough data for that, another approach can be used called calibration.

Transportation cost

When shipping goods from region \(r\) to \(r'\), we assume there are transportation costs. A simple form is just to use constant unit shipping costs \(\color{darkblue}{tc}_{c,r,r'}\). There are some interesting cases to consider [2]:

• \(\color{darkred}{P}_{c,r}+\color{darkblue}{tc}_{c,r,r'}\lt \color{darkred}{P}_{c,r'}\). This means there is a profit to be made by shipping more from \(r \rightarrow r'\). That means we are not in equilibrium: we will start shipping leading to other prices and quantities. Or stated differently: we are violating the zero-profit equilibrium condition.
• \(\color{darkred}{P}_{c,r}+\color{darkblue}{tc}_{c,r,r'}\gt \color{darkred}{P}_{c,r'}\). This means that the price differential is not large enough to pay for the shipping cost. The result should be: no shipping from \(r \rightarrow r'\), or \(\color{darkred}x_{c,r,r'}=0\) where \(\color{darkred}x_{c,r,r'}\) indicate our trade flows.
• \(\color{darkred}{P}_{c,r}+\color{darkblue}{tc}_{c,r,r'}= \color{darkred}{P}_{c,r'}\). This case allows for shipping: \(\color{darkred}x_{c,r,r'}\ge 0\).

Altogether we can now write: \[\color{darkred}{P}_{c,r}+\color{darkblue}{tc}_{c,r,r'}\ge \color{darkred}{P}_{c,r'} \perp \color{darkred}x_{c,r,r'} \ge 0\] This is notation for a complementarity condition. It means:

• \(\color{darkred}x_{c,r,r'}\gt 0 \Rightarrow \color{darkred}{P}_{c,r}+\color{darkblue}{tc}_{c,r,r'} = \color{darkred}{P}_{c,r'} \) and
• \( \color{darkred}{P}_{c,r}+\color{darkblue}{tc}_{c,r,r'} \gt \color{darkred}{P}_{c,r'} \Rightarrow \color{darkred}x_{c,r,r'}= 0\)

You may recognize this as complementarity from your linear programming textbook. In that context we would say \(\color{darkred}x_{c,r,r'}\) is the dual of the constraint \(\color{darkred}{P}_{c,r}+\color{darkblue}{tc}_{c,r,r'} \ge \color{darkred}{P}_{c,r'}\).  There we would say: if the dual \(\color{darkred}x_{c,r,r'}\gt 0 \), it is non-basic, and the constraint will be binding. And if the constraint is non-binding, the dual will be basic and \(\color{darkred}x_{c,r,r'} = 0\). Here we derived the same thing using economics.

The equilibrium conditions for the transportation cost are interesting and intuitive. 

Other equilibrium conditions

The other constraints are implemented as equality constraints. That is a bit of a shortcut: we can also implement them as proper equilibrium (complementarity) conditions. I believe the author of [1] meant these constraints always to be binding.

The complete model looks like:

Spatial Equilibrium Model
Sets
\(c,c'\)	Commodities
\(r,r'\)	Regions
Variables
\(\color{darkred}{Q}^{\color{darkred}s}_{c,r}\)	Supply quantities
\(\color{darkred}{Q}^{\color{darkred}d}_{c,r}\)	Demand quantities
\(\color{darkred}{P}_{c,r}\)	Prices
\(\color{darkred}{x}_{c,r,r'}\)	Shipped quantities
Equations
\[\color{darkred}{Q}^{\color{darkred}s}_{c,r} = \color{darkblue}\alpha_{c,r} + \sum_{c'}\color{darkblue}\beta_{c,r,c'}\color{darkred}{P}_{c',r}\]	Supply equation
\[\color{darkred}{Q}^{\color{darkred}d}_{c,r} = \color{darkblue}a_{c,r} + \sum_{c'}\color{darkblue}b_{c,r,c'}\color{darkred}{P}_{c',r}\]	Demand equation
\[\color{darkred}{Q}^{\color{darkred}s}_{c,r} + \sum_{r'}\color{darkred}x_{c,r',r}= \color{darkred}{Q}^{\color{darkred}d}_{c,r} + \sum_{r'}\color{darkred}x_{c,r,r'}\]	Flow balance (production + import = consumption + export)
\[\color{darkred}{P}_{c,r} + \color{darkblue}{tc}_{c,r,r'} \ge \color{darkred}{P}_{c,r'} \perp \color{darkred}x_{r,r',c}\ge 0\]	Transportation
\[\color{darkred}{x}_{c,r,r} = 0\]	Exclude diagonal

This is not an optimization model but rather a (linear) complementarity model: a square system of equations with complementarity conditions. We need to solve it with an appropriate solver. These models can also be solved using Quadratic Programming (QP) solver [4].

Data

To try out this model, I used the small data set from [3]. 

I organized this as:

----     84 PARAMETER coeff  coefficients for demand and supply functions

INDEX 1 = Demand

                       Intercept       Wheat  FeedGrains        Beef

Wheat     .US          15364.000      -4.960
Wheat     .EEC         14383.000      -3.400
Wheat     .UKIreland    4427.000      -1.290
Wheat     .Other       31731.000
FeedGrains.US         140556.000               -1224.000      48.130
FeedGrains.EEC         31694.000                -157.000      10.680
FeedGrains.UKIreland   12720.000                 -63.000       5.820
Beef      .US          14190.000                              -6.950
Beef      .EEC          6830.000                              -3.290
Beef      .UKIreland    2178.000                              -1.420

INDEX 1 = Supply

                       Intercept       Wheat  FeedGrains        Beef

Wheat     .US          18520.000     427.000    -190.000
Wheat     .EEC         12655.000     213.000     -74.000
Wheat     .UKIreland    1441.000      30.000      -8.000
FeedGrains.US          98438.000    -694.000    2163.000
FeedGrains.EEC         16531.000     -85.000     207.000
FeedGrains.UKIreland    5446.000     -35.000      68.000
FeedGrains.Other        2479.000
Beef      .US           6536.000                 -84.000       5.900
Beef      .EEC          3235.000                 -24.000       2.900
Beef      .UKIreland     808.000                  -6.000       1.000
Beef      .Other         584.000


----     84 PARAMETER transCost  Transportation Cost Matrix

                              US         EEC   UKIreland       Other

Wheat     .US                          8.438       8.030      15.000
Wheat     .EEC             8.438                   0.420      15.000
Wheat     .UKIreland       8.030       0.420                  15.000
Wheat     .Other          15.000      15.000      15.000
FeedGrains.US                          8.438       8.030      15.000
FeedGrains.EEC             8.438                   0.420      15.000
FeedGrains.UKIreland       8.030       0.420                  15.000
FeedGrains.Other          15.000      15.000      15.000
Beef      .US                         84.802      80.702     100.000
Beef      .EEC            84.802                   4.221     100.000
Beef      .UKIreland      80.702       4.221                 100.000
Beef      .Other         100.000     100.000     100.000
Grain     .US                          8.438       8.030      15.000
Grain     .EEC                                     0.420      15.000
Grain     .UKIreland                                          15.000

This leads to a square system of equations with 72 variables and 72 equations.

Reproducibility

The solution reported in [3] is a bit sloppy. It is somewhat infeasible. 

When I set my initial values to this solution, and solve with iteration limit 0 (that means: just check the initial values, don't solve), we see the following. First I look at the solution. There are infeasibilities related to the demand and supply functions:

---- EQU supply  supply function

                            LOWER          LEVEL          UPPER         MARGINAL

US       .Wheat          18520.0000     18517.7800     18520.0000     39048.0000 INFES
US       .FeedGrains     98438.0000     98451.1500     98438.0000    143757.0000 INFES
US       .Beef            6536.0000      6535.3390      6536.0000      7854.0000 INFES
EEC      .Wheat          12655.0000     12653.9000     12655.0000     23152.0000 INFES
EEC      .FeedGrains     16531.0000     16531.5100     16531.0000     21370.0000 INFES
EEC      .Beef            3235.0000      3234.9310      3235.0000      4203.0000 INFES
UKIreland.Wheat           1441.0000      1441.2800      1441.0000      3059.0000 INFES
UKIreland.FeedGrains      5446.0000      5446.0200      5446.0000      6519.0000 INFES
UKIreland.Beef             808.0000       808.1700       808.0000      1256.0000 INFES
Other    .Wheat               .              .              .              .          
Other    .FeedGrains      2479.0000      2479.0000      2479.0000      2479.0000      
Other    .Beef             584.0000       584.0000       584.0000       584.0000      

---- EQU demand  demand function

                            LOWER          LEVEL          UPPER         MARGINAL

US       .Wheat         -15364.0000    -15364.1216    -15364.0000     15032.0000 INFES
US       .FeedGrains   -140556.0000   -140550.4133   -140556.0000    128448.0000 INFES
US       .Beef          -14190.0000    -14189.7505    -14190.0000      8438.0000 INFES
EEC      .Wheat         -14383.0000    -14382.6640    -14383.0000     14155.0000 INFES
EEC      .FeedGrains    -31694.0000    -31693.2192    -31694.0000     31768.0000 INFES
EEC      .Beef           -6830.0000     -6830.3249     -6830.0000      4347.0000 INFES
UKIreland.Wheat          -4427.0000     -4427.9202     -4427.0000      4341.0000 INFES
UKIreland.FeedGrains    -12720.0000    -12719.5462    -12720.0000     13909.0000 INFES
UKIreland.Beef           -2178.0000     -2177.8378     -2178.0000      1112.0000 INFES
Other    .Wheat         -31731.0000    -31731.0000    -31731.0000     31731.0000      
Other    .FeedGrains          .              .              .              .          
Other    .Beef                .              .              .              .          

We can also look at the equation listing to see the same:

 

---- supply  =E=  supply function

supply(US,Wheat)..  Qs(US,Wheat) - 427*P(US,Wheat) + 190*P(US,FeedGrains) =E= 18520 ;
     
      (LHS = 18517.78, INFES = 2.22000000000116 ****)
     
supply(US,FeedGrains)..  Qs(US,FeedGrains) + 694*P(US,Wheat) - 2163*P(US,FeedGrains) =E= 98438 ;
     
      (LHS = 98451.15, INFES = 13.1499999999942 ****)
     
supply(US,Beef)..  Qs(US,Beef) + 84*P(US,FeedGrains) - 5.9*P(US,Beef) =E= 6536 ;
     
      (LHS = 6535.339, INFES = 0.661000000000968 ****)

---- demand  =E=  demand function

demand(US,Wheat)..  - Qd(US,Wheat) - 4.96*P(US,Wheat) =E= -15364 ; (LHS = -15364.1216, INFES = 0.121600000000399 ****)
     
demand(US,FeedGrains)..  - Qd(US,FeedGrains) - 1224*P(US,FeedGrains) + 48.13*P(US,Beef) =E= -140556 ;
     
      (LHS = -140550.4133, INFES = 5.58670000001439 ****)
     
demand(US,Beef)..  - Qd(US,Beef) - 6.95*P(US,Beef) =E= -14190 ; (LHS = -14189.7505, INFES = 0.249499999999898 ****)
     

Let's verify the first supply equation. The regression equation looks like: \[S_{11}=18,520+427 P_{11}-190 P_{21}\] In the equation listing we see, this arrived in GAMS as: 

supply(US,Wheat)..  Qs(US,Wheat) - 427*P(US,Wheat) + 190*P(US,FeedGrains) =E= 18520 ;

This is the same, just reorganized a little bit. When we plug in the solution values:

Qs(US,Wheat)      39048

P(US,Wheat)       66.96

P(US,FeedGrains)  42.43

we get a value of 18517.78, which is a little bit infeasible (it should be 18520).

The infeasibilities are small, so the impact on the solution should also be small. 

----    197 PARAMETER mysol  our solution

                                US         EEC   UKIreland       Other  production       price

Wheat     .US            15032.000                           24015.787   39047.685      66.956
Wheat     .EEC                       14155.000    1281.518    7715.213   23152.080      66.956
Wheat     .UKIreland                              3059.000                3058.567      67.376
Wheat     .Other                                                                        81.956
Wheat     .consumption   15031.898   14155.349    4340.085   31731.000
FeedGrains.US           128448.000    7919.037    7389.745              143756.597      42.435
FeedGrains.EEC                       21370.000                           21370.368      50.873
FeedGrains.UKIreland                              6519.000                6519.432      50.465
FeedGrains.Other                      2479.000                            2479.000      35.873
FeedGrains.consumption  128447.815   31768.404   13909.177
Beef      .US             7854.000                                        7854.261     827.588
Beef      .EEC                        4203.000                            4203.016     754.814
Beef      .UKIreland                   143.647    1112.000                1255.805     750.593
Beef      .Other           584.000                                         584.000     727.588
Beef      .consumption    8438.261    4346.663    1112.158

Complementarity in the solution

The results for equation \[\color{darkred}{P}_{c,r} - \color{darkred}{P}_{c,r'}   \ge -\color{darkblue}{tc}_{c,r,r'} \perp \color{darkred}x_{r,r',c}\ge 0\] are:

---- EQU trade  prices

                                      LOWER          LEVEL          UPPER         MARGINAL

Wheat     .US       .EEC              -8.4380          .            +INF             .          
Wheat     .US       .UKIreland        -8.0300        -0.4200        +INF             .          
Wheat     .US       .Other           -15.0000       -15.0000        +INF        24015.7872      
Wheat     .EEC      .US               -8.4380          .            +INF             .          
Wheat     .EEC      .UKIreland        -0.4200        -0.4200        +INF         1281.5180      
Wheat     .EEC      .Other           -15.0000       -15.0000        +INF         7715.2128      
Wheat     .UKIreland.US               -8.0300         0.4200        +INF             .          
Wheat     .UKIreland.EEC              -0.4200         0.4200        +INF             .          
Wheat     .UKIreland.Other           -15.0000       -14.5800        +INF             .          
Wheat     .Other    .US              -15.0000        15.0000        +INF             .          
Wheat     .Other    .EEC             -15.0000        15.0000        +INF             .          
Wheat     .Other    .UKIreland       -15.0000        14.5800        +INF             .          
FeedGrains.US       .EEC              -8.4380        -8.4380        +INF         7919.0367      
FeedGrains.US       .UKIreland        -8.0300        -8.0300        +INF         7389.7450      
FeedGrains.US       .Other           -15.0000         6.5620        +INF             .          
FeedGrains.EEC      .US               -8.4380         8.4380        +INF             .          
FeedGrains.EEC      .UKIreland        -0.4200         0.4080        +INF             .          
FeedGrains.EEC      .Other           -15.0000        15.0000        +INF             .          
FeedGrains.UKIreland.US               -8.0300         8.0300        +INF             .          
FeedGrains.UKIreland.EEC              -0.4200        -0.4080        +INF             .          
FeedGrains.UKIreland.Other           -15.0000        14.5920        +INF             .          
FeedGrains.Other    .US              -15.0000        -6.5620        +INF             .          
FeedGrains.Other    .EEC             -15.0000       -15.0000        +INF         2479.0000      
FeedGrains.Other    .UKIreland       -15.0000       -14.5920        +INF             .          
Beef      .US       .EEC             -84.8020        72.7746        +INF             .          
Beef      .US       .UKIreland       -80.7020        76.9956        +INF             .          
Beef      .US       .Other          -100.0000       100.0000        +INF             .          
Beef      .EEC      .US              -84.8020       -72.7746        +INF             .          
Beef      .EEC      .UKIreland        -4.2210         4.2210        +INF             .          
Beef      .EEC      .Other          -100.0000        27.2254        +INF             .          
Beef      .UKIreland.US              -80.7020       -76.9956        +INF             .          
Beef      .UKIreland.EEC              -4.2210        -4.2210        +INF          143.6465      
Beef      .UKIreland.Other          -100.0000        23.0044        +INF             .          
Beef      .Other    .US             -100.0000      -100.0000        +INF          584.0000      
Beef      .Other    .EEC            -100.0000       -27.2254        +INF             .          
Beef      .Other    .UKIreland      -100.0000       -23.0044        +INF             .          

Note that the column MARGINAL prints the levels of the variable \(\color{darkred}x_{r,r',c}\). Indeed we can see that shipping occurs (\(\color{darkred}x_{r,r',c}\gt 0\)) only when the constraint is binding. And the reverse: for all cases where the constraint level is not at its lower bound, the variable \(\color{darkred}x_{r,r',c}=0\). This report is just like for an LP, except that the dual (or marginal) is now an explicit model variable.

Conclusion

Here we solved the problem from [3] as a square system of equations. The solution reported in [3] is slightly infeasible. I suspect this is due to using software and hardware with more limited precision in 1966 than we have access to these days. I further suspect the model was solved as a QP by integrating the problem. That was the main approach before complementarity solvers became available.

This simple equilibrium model shows how can we find an equilibrium solution that solves simultaneously for prices, demand and supply quantities, and trade patterns. These types of models are used quite a lot. 

It is a good example of modeling complementarity explicitly: if the price differential between supply and demand in two regions is too small, we don't trade.

References

1. Giffen goods, https://www.investopedia.com/terms/g/giffen-good.asp
2. Samuelson, Paul A., "Spatial Price Equilibrium and Linear Programming," Am. Econ. Rev. 42:283-303, June 1952
3. D. Lee Bawden, "A Spatial Price Equilibrium Model of International Trade", American Journal of Agricultural Economics, Volume 48, November 1966, Pages 862-874
4. Solving Linear Complementarity Problems without an LCP Solver, https://yetanothermathprogrammingconsultant.blogspot.com/2021/05/solving-linear-complementarity-problems.html

Appendix. GAMS Model

$ontext    Spatial Equilibrium    Quick and dirty model    (Only "true" complementarity for trade, the rest are equalities)    Data from:    D. Lee Bawden    A Spatial Price Equilibrium Model of International Trade    American Journal of Agricultural Economics    Volume 48, November 1966, Pages 862-874 $offtext *--------------------------------------------------------------- * Data *--------------------------------------------------------------- set    dummy 'for better display' /Intercept/    c 'commodities' /Wheat, FeedGrains, Beef/    r 'regions' /US, EEC, UKIreland, Other/    g(c) 'grains' /Wheat, FeedGrains/ ; * demand/supply as (linear) function of prices table coeff(*,c,r,*) 'coefficients for demand and supply functions'                             Intercept   Wheat    FeedGrains    Beef Demand.Wheat.US              15364      -4.96 Demand.Wheat.EEC             14383      -3.40 Demand.Wheat.UKIreland        4427      -1.29 Demand.Wheat.Other           31731 Demand.FeedGrains.US        140556               -1224        48.13 Demand.FeedGrains.EEC        31694                -157        10.68 Demand.FeedGrains.UKIreland  12720                 -63         5.82 Demand.FeedGrains.Other Demand.Beef.US               14190                            -6.95 Demand.Beef.EEC               6830                            -3.29 Demand.Beef.UKIreland         2178                            -1.42 Demand.Beef.Other Supply.Wheat.US              18520        427     -190 Supply.Wheat.EEC             12655        213      -74 Supply.Wheat.UKIreland        1441         30       -8 Supply.Wheat.Other Supply.FeedGrains.US         98438       -694     2163 Supply.FeedGrains.EEC        16531        -85      207 Supply.FeedGrains.UKIreland   5446        -35       68 Supply.FeedGrains.Other       2479 Supply.Beef.US                6536                 -84          5.9 Supply.Beef.EEC               3235                 -24          2.9 Supply.Beef.UKIreland          808                  -6          1.0 Supply.Beef.Other              584 ; alias(r,rr); table transCost(*,r,rr) 'Transportation Cost Matrix'                       US     EEC    UKIreland    Other Beef.US                     84.802   80.702     100.000 Beef.EEC                              4.221     100.000 Beef.UKIreland                                  100.000 Beef.Other Grain.US                     8.438    8.030      15.000 Grain.EEC                             0.420      15.000 Grain.UKIreland                                  15.000 Grain.Other ; alias(c,cc); * set the transportation cost for the individual grains * and use transCost(g,r,rr) = transCost('Grain',r,rr); transCost(c,r,rr)$(transCost(c,r,rr)=0) = transCost(c,rr,r); display  coeff,transCost; *----------------------------------------------------------------------- * spatial equilibrium *----------------------------------------------------------------------- positive variables    Qd(c,r)      'demand quantities at demand regions'    Qs(c,r)      'supply quantities at supply regions'    P(c,r)       'price'    X(c,r,rr)    'quantities traded/shipped' ; equations    supply(c,r)     'supply function'    demand(c,r)     'demand function'    flows(c,r)      'trade flows'    trade(c,r,rr)   'prices' ; supply(c,r)..    Qs(c,r) =e= coeff('supply',c,r,'intercept')                 + sum(cc,coeff('supply',c,r,cc)*P(cc,r)); demand(c,r)..      coeff('demand',c,r,'intercept')      + sum(cc,coeff('demand',c,r,cc)*P(cc,r)) =e= Qd(c,r); flows(c,r)..       Qs(c,r) + sum(rr, X(c,rr,r)) =e= Qd(c,r) + sum(rr, X(c,r,rr)); * this is true complementarity equation: *       trade(r,rr,c) >= 0 compl. X(c,r,rr) >= 0 * only one can be non-binding trade(c,r,rr)..    P(c,r) + transCost(c,r,rr) =g= P(c,rr); * "shipping" means here: trade between different regions * so fix x=0 if we deal with the same region x.fx(c,r,r) = 0; model lcp /supply.Qs, demand.Qd, flows.P, trade.x/; *----------------------------------------------------------------------- * check solution from Bawden *----------------------------------------------------------------------- table sol(c,*,*)  'solution from Bawden'                             US     EEC    UKIreland    Other    production  price Wheat.US                   15032                       24016      39048     66.96 Wheat.EEC                         14155    1282         7715      23152     66.96 Wheat.UKIreland                            3059                    3059     67.38 Wheat.Other                                                                 81.96 Wheat.consumption          15032  14155    4341        31731 FeedGrains.US             128448   7919    7390                  143757     42.43 FeedGrains.EEC                    21370                           21370     50.87 FeedGrains.UKIreland                       6519                    6519     50.46 FeedGrains.Other                   2479                            2479     35.87 FeedGrains.Consumption    128448  31768   13909                  174125 Beef.US                     7854                                   7854    827.59 Beef.EEC                           4203                            4203    754.81 Beef.UKIreland                      144    1112                    1256    750.59 Beef.Other                   584                                    584    727.59 Beef.Consumption            8438   4347    1112 ; display sol; * set initial values x.l(c,r,rr)$(not sameas(r,rr)) = sol(c,r,rr); Qs.l(c,r) = sol(c,r,'production'); Qd.l(c,r) = sol(c,'consumption',r); P.l(c,r) = sol(c,r,'price'); * iterlim = 0 so solver will only check initial solution * inspect the listing file option limrow=9999,iterlim=0; solve lcp using mcp; *----------------------------------------------------------------------- * compute equilibrium *----------------------------------------------------------------------- option iterlim=99999; solve lcp using mcp; *----------------------------------------------------------------------- * reporting *----------------------------------------------------------------------- parameter mysol(c,*,*)  'our solution'; mysol(c,r,rr) = x.l(c,r,rr); mysol(c,r,r) = Qs.l(c,r) - sum(rr$(not sameas(r,rr)),x.l(c,r,rr)); mysol(c,r,'production') = Qs.l(c,r); mysol(c,'consumption',r) = Qd.l(c,r); mysol(c,r,'price') = P.l(c,r); display mysol;