In [1], I discussed a model for the Euclidean Streiner Tree problem. A non-convex integer programming model from the literature was reformulated into a MISOCP (not a version of a Japanese dish, but a Mixed-Integer Second-Order Cone Program). Together with a symmetry-breaking constraint and some high-performance solvers, this can lead to being able to solve larger models.
One of the disadvantages of the model in [1] is that it only works with the full number of Steiner points \(n-2\) where \(n\) is the number of given (original) points. Here I want to discuss how we can use Minimum Spanning Tree (MST) models [2], as a building block for a model where we can add just a few Steiner points. One reason this is interesting: the first few Steiner points have the most impact on the objective.
We can just pick any model from [2]. Let's use the single-commodity flow model:
| MST: Single-commodity flow formulation |
|---|
| \[\begin{align}\min\>&\color{darkred}z = \sum_{(i,j)\in \color{darkblue}A} \color{darkblue}c_{i,j}\color{darkred}x_{i,j}\\& \sum_{j|(i,j)\in \color{darkblue}A}\color{darkred}f_{i,j}=\sum_{j|(j,i)\in\color{darkblue}A}\color{darkred}f_{j,i} + \color{darkblue}b_{i} && \forall i \\ & \color{darkblue}M\cdot \color{darkred}x_{i,j} \ge \color{darkred}f_{i,j} && \forall (i,j) \in \color{darkblue}A \\ & \color{darkred}x_{i,j}\in \{0,1\}\\ & \color{darkred}f_{i,j} \in \{0,1,2,\dots,\color{darkblue}n-1\}\end{align}\] |
| MISOCP Model |
|---|
| \[\begin{align}\min\>&\color{darkred}z = \sum_{(i,j)\in \color{darkblue}A_1} \color{darkblue}c_{i,j}\color{darkred}x_{i,j} + \sum_{(i,j)\in \color{darkblue}A_2} \color{darkred}d_{i,j}\\ & \color{darkred}d_{i,j}\ge \color{darkred}\Delta_{i,j}- \color{darkblue}M_1(1-\color{darkred}x_{i,j}) && \forall (i,j)\in \color{darkblue}A_2 \\ & \color{darkred}\Delta^2_{i,j} \ge \sum_c \color{darkred}\delta^2_{i,j,c} && \forall (i,j) \in \color{darkblue}A_2 \\ & \color{darkred}\delta_{i,j,c} = \color{darkred}p_{i,c}-\color{darkred}p_{j,c} && \forall (i,j)\in \color{darkblue}A_2, c \in \{x,y\} \\& \sum_{j|(i,j)\in \color{darkblue}A}\color{darkred}f_{i,j}=\sum_{j|(j,i)\in\color{darkblue}A}\color{darkred}f_{j,i} + \color{darkblue}b_{i} && \forall i \\ & \color{darkblue}M_2\cdot \color{darkred}x_{i,j} \ge \color{darkred}f_{i,j} && \forall (i,j) \in \color{darkblue}A \\ & \color{darkred}p_{i,c}=\color{darkblue}p^0_{i,c} && \text{for given points} \\ & \color{darkred}p_{i,c} \in [\color{darkblue}L,\color{darkblue}U] && \text{for Steiner points} \\ & \color{darkred}p_{i,x} \le \color{darkred}p_{i+1,x} && \text{for Steiner points}\\ & \color{darkred}d_{i,j},\color{darkred}\Delta_{i,j}\ge 0 \\ & \color{darkred}x_{i,j}\in \{0,1\}\\ & \color{darkred}f_{i,j} \in \{0,1,2,\dots,\color{darkblue}n-1\}\end{align}\] |
The first three constraints can be combined into \[\color{darkred}d_{i,j} \ge \sqrt{\sum_c\left(\color{darkred}p_{i,c}-\color{darkred}p_{j,c}\right)^2}-\color{darkblue}M(1-\color{darkred}x_{i,j})\] Splitting it in three components can help the solver recognize this as a convex quadratic constraint. Note that the variables \(\color{darkred}p_{i,c}, c\in \{x,y\}\), indicating the position of point \(i\), are constant for the original points and are unknown for the Steiner points. The Steiner points must lie in the convex hull of the given points, so we can deduce lower- and upper-bounds for them. The lowerbound is the smallest \(x/y\) coordinate of the given points, and the upperbound is the largest. We order the Steiner points by \(x\) coordinate.
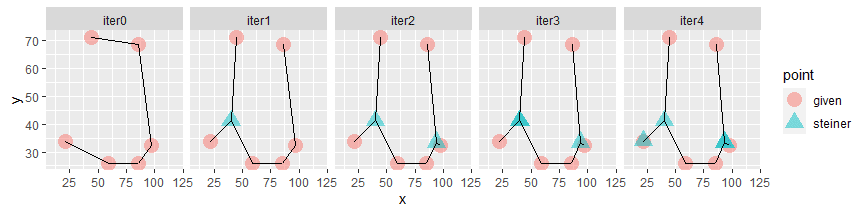
The first Steiner point is really helpful. After that, they do contribute little if anything. We see that Steiner points start to overlap previous points.
---- 198 PARAMETER Objs iter0 157.441, iter1 151.967, iter2 151.426, iter3 151.426, iter4 151.426 ---- 198 PARAMETER Points INDEX 1 = iter0 x y p1.given 85.283 26.044 p2.given 97.182 32.402 p3.given 21.663 33.972 p4.given 86.101 68.526 p5.given 44.485 71.240 p6.given 59.008 26.009 INDEX 1 = iter1 x y p1.given 85.283 26.044 p2.given 97.182 32.402 p3.given 21.663 33.972 p4.given 86.101 68.526 p5.given 44.485 71.240 p6.given 59.008 26.009 s1.steiner 39.971 41.171 INDEX 1 = iter2 x y p1.given 85.283 26.044 p2.given 97.182 32.402 p3.given 21.663 33.972 p4.given 86.101 68.526 p5.given 44.485 71.240 p6.given 59.008 26.009 s1.steiner 39.972 41.171 s2.steiner 93.599 33.559 INDEX 1 = iter3 x y p1.given 85.283 26.044 p2.given 97.182 32.402 p3.given 21.663 33.972 p4.given 86.101 68.526 p5.given 44.485 71.240 p6.given 59.008 26.009 s1.steiner 39.971 41.171 s2.steiner 39.971 41.171 s3.steiner 93.599 33.559 INDEX 1 = iter4 x y p1.given 85.283 26.044 p2.given 97.182 32.402 p3.given 21.663 33.972 p4.given 86.101 68.526 p5.given 44.485 71.240 p6.given 59.008 26.009 s1.steiner 21.663 33.972 s2.steiner 39.971 41.171 s3.steiner 93.599 33.559 s4.steiner 93.599 33.559
This would mean that we don't really need to solve problems with a large number of Steiner points. Just enough, until the objective does not improve anymore. This is a bit like the statistical techniques for clustering data. There also: we typically start with a small number of clusters, and stop once, by some measure, the situation does not sufficiently improve anymore.
Note: The Steiner points are never fixed. So in principle, they can be moved around from one iteration to the next. We see that does not happen here. A good Steiner point stays put (the ordering constraint may give it a different label). This behavior is likely problem dependent.
Conclusion
We can augment an MST (Minimum Spanning Tree) model to allow for Steiner points. As it seems that the value of adding additional Steiner points diminishes quickly, we can get good improvements by just adding a few Steiner points.
I think this was an interesting experiment.
References
- Euclidean Steiner tree problems as MISOCP, https://yetanothermathprogrammingconsultant.blogspot.com/2021/03/euclidean-steiner-tree-problems-as.html
- Minimum Spanning Trees in Math Programming models, https://yetanothermathprogrammingconsultant.blogspot.com/2021/03/minimum-spanning-trees-in-math.html

No comments:
Post a Comment