The 8-queens problem without binary variables

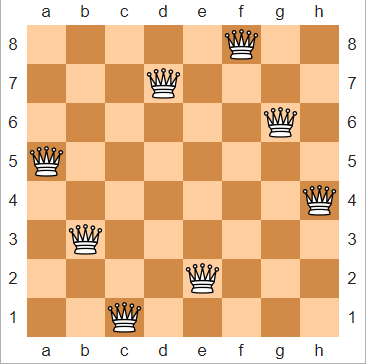
An eight-queens solution [3]

The 8-queens problem can be stated as:

Place \(n=8\) queens on an \(n \times n\) board such that none of the queens is attacked by another. 

This is a feasibility problem, and can be formulated as a MIP problem [1]:

n-Queens Problem
\[\begin{align}& \sum_j \color{DarkRed}x_{i,j} = 1 && \forall i\\& \sum_i \color{DarkRed}x_{i,j} = 1 && \forall j\\ & \sum_{i-j=k} \color{DarkRed}x_{i,j} \le 1 && k=-(n-2),\dots,(n-2)\\& \sum_{i+j=k} \color{DarkRed}x_{i,j} \le 1 && k=3,\dots,2n-1\\ & \color{DarkRed}x_{i,j}\in\{0,1\} \end{align}\]

Basically: place a single queen on each row and column such that each they don't attack each other diagonally. We need the conditions \(x_{i,j}\in \{0,1\}\) to make sure the variables only assume the values zero or one. If we would drop this requirement, and only assume \(x_{i,j}\in [0,1]\) (i.e. they have lower- and upper-bounds of 0 and 1), we may see a fractional solution like:

----     39 VARIABLE x.L  

            c1          c2          c3          c4          c5          c6          c7          c8

r1                                                                               1.000
r2                               0.200       0.800
r3       0.600       0.300                   0.100
r4                                                       0.600                               0.400
r5       0.200       0.700                   0.100
r6       0.200                                           0.400       0.400
r7                               0.800                               0.200
r8                                                                   0.400                   0.600

Nonlinear objective

We can invent a non-linear objective, to make sure the variables \(x_{i,j}\) assume only values zero or one in the optimal solution: \[\max \sum_{i,j} x^2_{i,j}\] The idea is that \[0.2^2+0.8^2=0.68 < 0^2+1^2 = 1\] So we want to solve:

n-Queens Problem as continuous NLP
\[\begin{align} \max & \sum_{i,j} \color{DarkRed}x^2_{i,j}\\ & \sum_j \color{DarkRed}x_{i,j} = 1 && \forall i\\& \sum_i \color{DarkRed}x_{i,j} = 1 && \forall j\\ & \sum_{i-j=k} \color{DarkRed}x_{i,j} \le 1 && k=-(n-2),\dots,(n-2)\\& \sum_{i+j=k} \color{DarkRed}x_{i,j} \le 1 && k=3,\dots,2n-1\\ & \color{DarkRed}x_{i,j}\in [0,1] \end{align}\]

This looks very ingenious. Unfortunately, the problem is non-convex, a complication that was forgotten in [2]. Solving a non-convex NLP problem like this to optimality will require a global solver. Indeed when solved with the solver BARON, I see:

----     39 VARIABLE x.L  

            c1          c2          c3          c4          c5          c6          c7          c8

r1                                                       1.000
r2                   1.000
r3                                                                                           1.000
r4       1.000
r5                                           1.000
r6                                                                               1.000
r7                               1.000
r8                                                                   1.000

Altogether, I believe this is not a very successful way to circumvent using binary variables. We make the problem not any easier by making it non-linear and non-convex.

Nonlinear constraint

Another way to replace binary variables by a continuous construct is to impose a constraint \[x(1-x)=0\] This also something I would not recommend. This constraint is also non-convex and needs a global solver unless you have a very good starting point (or unless you are extremely lucky).

Conclusion

There are ways to formulate models with binary variables as continuous models using clever objectives or constraints. These tricks make the model not any easier: they introduce nasty non-convexities. It is better to use explicit binary variables, not in the least to make clear we are dealing with a combinatorial problem.

References

1. Chess and solution pool, http://yetanothermathprogrammingconsultant.blogspot.com/2018/11/chess-and-solution-pool.html discusses \(n\)-queens and related problems, and tries the solution pool to enumerate all possible solutions.
2. How to solve the 8 queens problem  with CVXPY? https://stackoverflow.com/questions/54652279/how-to-solve-the-8-queens-problem-with-cvxpy/54660353 proposes a novel way to prevent binary variables.
3. Eight queens puzzle, https://en.wikipedia.org/wiki/Eight_queens_puzzle