
From [1]:
I have the following problem:
- I have N square paper documents with side lengths between 150mm and 860mm. I know each document side's length.
- I need to create 3−4 differently sized boxes to fit all the documents, e.g. Three box types: Box 1 side L1=300mm, Box 2 side L2=600mm, Box 3: L3=860mm.
- There are as many boxes as documents, i.e. each document goes into its own separate box (of the smallest possible size so as to minimize waste of cardboard).
- What is the best way to decide on the size of the boxes, so as to minimize the total amount of (surface area) of cardboard used?
The data looks like:
 |
| Original Data (partial view) |
We have 1166 records. We see there are items with the same length. These duplicates will always go in the same box type. So we don't have to distinguish them in the optimization model. As a result, we can reorganize the data into unique values and their count:
--- 392 PARAMETER data size count i1 156.000 1.000 i2 162.000 1.000 i3 168.000 1.000 i4 178.000 2.000 i5 180.000 1.000 i6 185.000 2.000 ... i379 806.000 1.000 i380 820.000 1.000 i381 823.000 1.000 i382 827.000 2.000 i383 855.000 2.000 i384 864.000 1.000
This table has 384 records. A big improvement over 1166 items! This will make our optimization models much smaller. Note that we make sure things are ordered by size (increasing). We will exploit this in one of the models below.
For small data sets we can easily enumerate all possible ways to use \(T\) different box sizes. Here we have \(n=6\) unique item sizes and \(T=3\) boxes:
We see that the best configuration is to have boxes of size 2, 6 and 9 with areas 4. 36 and 81.
We assume throughout that each box is used for at least one item. This makes sense: when adding a new box size, it is never a good idea not to use it. Remember: box sizes are variable: we determine the size of a box (it is not given).
Some more observations:
For large problems, of course, complete enumeration is out of the question. We will need to do something more cleverly.
It is tempting to start with an assignment variable such as: \[x_{i,j} = \begin{cases} 1 & \text{if item $i$ is assigned to box type $j=1,\dots\,T$}\\ 0 & \text{otherwise}\end{cases}\] Here \(T\) is the number of differently sized boxes. Furthermore let \[a_j = \text{area of box $j$}\] This can lead to a model like: \[\bbox[lightcyan,10px,border:3px solid darkblue] {\begin{align}\min & \sum_{i,j} \> \mathit{count}_i \> a_j \> x_{i,j} \\ & \sum_j x_{i,j} = 1 & \forall i & \> \> \text{(assignment)} \\ & x_{i,j} = 1 \Rightarrow a_j \ge \mathit{size}_i^2 & &\>\>\text{(fit)} \\ & x_{i,j} \in \{0,1\} \\ & a_j \ge 0 && \>\>\text{(area of box type $j$)}\end{align}}\] This is problematic: we have a non-convex quadratic objective. This model can be linearized with some effort. First we introduce a variable \(y_{i,j}=a_j x_{i,j}\). As we are minimizing, we can get away with just \(y_{i,j} \ge a_j - M (1-x_{i,j})\). The linearized model can look like \[\bbox[lightcyan,10px,border:3px solid darkblue] {\begin{align}min & \sum_{i,j} \> \mathit{count}_i \> y_{i,j} \\ & a_j \ge \mathit{size}_i^2 \> x_{i,j} \\ & y_{i,j} \ge a_j - \mathit{Amax} (1-x_{i,j}) \\ & a_1 = \mathit{Amax} \\ & a_{j+1} \le a_j - 1 \end{align}}\] where \(\mathit{Amax}=864^2\). The last two constraints should help the solver a little bit: we reduce symmetry.
This model is very difficult to solve. After 20 minutes it still had a gap of 30%.
This model is organized around the variable \[x_{i,j} = \begin{cases} 1 & \text{if items $i$ through $j$ are put in the same size box (with size $j$)} \\ 0 & \text{otherwise}\end{cases}\] This is somewhat unusual, but we'll see this will make a rather nice MIP model. Here we also see why the ordering of items by size is a useful concept: if \(x_{i,j}=1\) then all items \(i,i+1,\dots,j-1,j\) are placed in the same size box.
The basic idea is to cover each item exactly once by a variable \(x_{i,j}\). In addition we want exactly \(T\) variables that have a value of one. Here is how we organize our variables \(x_{i,j}\):
A feasible solution has two properties:
Indeed the total cost (area) goes up. Interestingly the smallest box size stays the same.
Notes:
This problem can also be modeled as a network problem. See [2] for more details.
The network is not very simple. Consider again the 6 item, \(T=3\) example. We drew a picture of a feasible covering earlier. The same feasible solution for the network of this problem looks like:
Selecting a link from item \(i\) to item \(j\) means: put items \(i,i+1,\dots,j-1\) into a box with size \(j-1\). Similarly, a link from item \(i\) to the sink node means: put items \(i,i+1,\dots,n\) into a box with size \(n\) (where \(n\) is the largest item or box).
The cost coefficients are defined by: \[\begin{align}c_{i,j} &= \mathit{size}_{j-1}^2 \sum_{k=i}^{j-1} \mathit{count}_k & \forall i\le j\\c_{i,\mathit{sink}} &= \mathit{size}_n^2 \sum_{k=i}^n \mathit{count}_k & \forall i \end{align}\]
We want to solve a shortest path problem from item 1 to the sink node with a side constraint: the number of "blue" nodes we visit should be exactly \(T\). The side constraint makes this a cardinality constrained or hop constrained shortest path problem. We can solve this as an MIP problem: \[\bbox[lightcyan,10px,border:3px solid darkblue] {\begin{align}min & \sum_{(i,j)\in A} c_{i,j} x_{i,j} \\ & \sum_{(j,i)\in A} x_{j,i} + b_i = y_i & \forall i & \>\> \text{(flow balance)}\\ & y_i = \sum_{(i,j)\in A} x_{i,j} & \forall i & \>\>\text{(outflow node $i$)}\\ &\sum_{i \ne \mathit{sink}} y_i = T &&\text{(cardinality)}\\ & x_{i,j},y_i \ge 0 \end{align} }\] Here \(b_i\) is the net exogenous supply of node \(i\). I.e. \[b_i = \begin{cases} 1 & \>\> \text{if $i=1$}\\ -1 & \>\> \text{if $i=\mathit{sink}$}\\ 0 & \>\>\text{otherwise}\end{cases}\]
This model solves very fast (the relaxed LP gives an integer solution for this data set). The solution for our real data with \(T=4\) looks like:
This means our optimal grouping is \(i_1 - i_{155}\), \(i_{156} - i_{268}\), \(i_{269} - i_{351}\), \(i_{352} - i_{384}\). This is the same solution as for our set partitioning model.
The previous model was a network model with a side constraint. We can create a pure network by augmenting the network. Basically we keep track of the number of different boxes by indexing the nodes by item number and layer number. This means we have a larger number of nodes. The network can look like:
Here we see all paths contain \(T=3\) blue nodes. Each node is labeled by (item,layer). Be aware that an arc \(i \rightarrow j\) represents putting items \(i,\dots,j-1\) in the same sized box. As nodes have 2 indices, arcs have four!
The results for the original data set with \(T=4\) looks like:
Note again that this must be interpreted as follows: group items \(i_1 - i_{155}\), \(i_{156} - i_{268}\), \(i_{269} - i_{351}\), \(i_{352} - i_{384}\) in box sizes large enough to hold \(i_{155}\), \(i_{268}\), \(i_{351}\), \(i_{384}\) . This is the same solution as for our earlier models.
As this is a pure network, we can ask Cplex to use the network simplex method to solve this. We see:
We see the presolver takes most of the time, but is also highly effective. The presolved model takes zero seconds to solve.
A dynamic programming algorithm is an alternative for this problem. If we define \[f_{i,b} = \text{minimum total area when we pack items $1,\dots,i$ (ordered and with unique size) in $b$ box sizes}\] then we can write down the recursion:\[ f_{i,b} = \min_{k=b-1,\dots,i-1} \left\{ f_{k,b-1} + \mathit{size}_i^2 \sum_{j=k+1}^i \mathit{count}_j \right\}\]
When we code this up in R we could see something like:
Note that the inner \(k\) loop is vectorized. The results look like:
The results for 1,2 and 3 boxes we get for free.
The data set used here is shown below:
Small data example
For small data sets we can easily enumerate all possible ways to use \(T\) different box sizes. Here we have \(n=6\) unique item sizes and \(T=3\) boxes:
 |
| Small data set with n=6, T=3 |
We assume throughout that each box is used for at least one item. This makes sense: when adding a new box size, it is never a good idea not to use it. Remember: box sizes are variable: we determine the size of a box (it is not given).
Some more observations:
- The larges box size is the size of the largest item.
- It will never make sense to choose a box size that is not equal to one of the item sizes. In this example: a box size of 3 will never be optimal.
For large problems, of course, complete enumeration is out of the question. We will need to do something more cleverly.
Assignment formulation
It is tempting to start with an assignment variable such as: \[x_{i,j} = \begin{cases} 1 & \text{if item $i$ is assigned to box type $j=1,\dots\,T$}\\ 0 & \text{otherwise}\end{cases}\] Here \(T\) is the number of differently sized boxes. Furthermore let \[a_j = \text{area of box $j$}\] This can lead to a model like: \[\bbox[lightcyan,10px,border:3px solid darkblue] {\begin{align}\min & \sum_{i,j} \> \mathit{count}_i \> a_j \> x_{i,j} \\ & \sum_j x_{i,j} = 1 & \forall i & \> \> \text{(assignment)} \\ & x_{i,j} = 1 \Rightarrow a_j \ge \mathit{size}_i^2 & &\>\>\text{(fit)} \\ & x_{i,j} \in \{0,1\} \\ & a_j \ge 0 && \>\>\text{(area of box type $j$)}\end{align}}\] This is problematic: we have a non-convex quadratic objective. This model can be linearized with some effort. First we introduce a variable \(y_{i,j}=a_j x_{i,j}\). As we are minimizing, we can get away with just \(y_{i,j} \ge a_j - M (1-x_{i,j})\). The linearized model can look like \[\bbox[lightcyan,10px,border:3px solid darkblue] {\begin{align}min & \sum_{i,j} \> \mathit{count}_i \> y_{i,j} \\ & a_j \ge \mathit{size}_i^2 \> x_{i,j} \\ & y_{i,j} \ge a_j - \mathit{Amax} (1-x_{i,j}) \\ & a_1 = \mathit{Amax} \\ & a_{j+1} \le a_j - 1 \end{align}}\] where \(\mathit{Amax}=864^2\). The last two constraints should help the solver a little bit: we reduce symmetry.
This model is very difficult to solve. After 20 minutes it still had a gap of 30%.
Covering formulation
This model is organized around the variable \[x_{i,j} = \begin{cases} 1 & \text{if items $i$ through $j$ are put in the same size box (with size $j$)} \\ 0 & \text{otherwise}\end{cases}\] This is somewhat unusual, but we'll see this will make a rather nice MIP model. Here we also see why the ordering of items by size is a useful concept: if \(x_{i,j}=1\) then all items \(i,i+1,\dots,j-1,j\) are placed in the same size box.
The basic idea is to cover each item exactly once by a variable \(x_{i,j}\). In addition we want exactly \(T\) variables that have a value of one. Here is how we organize our variables \(x_{i,j}\):
 |
| Variables x(i,j) |
A feasible solution has two properties:
- Each item (column) selects exactly one variable (row),
- The total number of selected variables is \(T\).
A feasible solution can look like:
 |
| Feasible solution for T=3 |
The feasible solution has exactly \(T=3\) variables selected, and all items are covered exactly once.
The complete model is surprisingly simple: \[\bbox[lightcyan,10px,border:3px solid darkblue] {\begin{align}min & \sum_{i\le j} c_{i,j} x_{i,j}\\ & \sum_{i \le k \le j} x_{i,j} = 1 & \forall k\\ & \sum_{i\le j} x_{i,j} = T \\ & x_{i,j} \in \{0,1\}\end{align}}\] The constraint \[\sum_{i \le k \le j} x_{i,j} = 1\>\>\> \forall k\] is typically a long summation. In the picture above, for \(k=2\), we have to add up the variables \(x_{1,2}\), \(x_{1,3}\), \(x_{1,4}\), \(x_{1,5}\), \(x_{1,6}\), \(x_{2,2}\), \(x_{2,3}\), \(x_{2,4}\), \(x_{2,5}\), and \(x_{2,6}\). The cost coefficients can be calculated as: \[c_{i,j} = \sum_{k=i}^j \mathit{count}_k \>\mathit{size}_j^2 \>\>\>\>\forall i\le j\] or if you prefer \[c_{i,j} = \mathit{size}_j^2 \sum_{i\le k\le j} \mathit{count}_k \ \>\>\>\>\forall i\le j\] This is like a set covering or better set partitioning problem (we want to cover exactly once: this is a set partitioning construct).
This leads to a large, but easy to solve MIP model: for \(T=4\), I see:
The complete model is surprisingly simple: \[\bbox[lightcyan,10px,border:3px solid darkblue] {\begin{align}min & \sum_{i\le j} c_{i,j} x_{i,j}\\ & \sum_{i \le k \le j} x_{i,j} = 1 & \forall k\\ & \sum_{i\le j} x_{i,j} = T \\ & x_{i,j} \in \{0,1\}\end{align}}\] The constraint \[\sum_{i \le k \le j} x_{i,j} = 1\>\>\> \forall k\] is typically a long summation. In the picture above, for \(k=2\), we have to add up the variables \(x_{1,2}\), \(x_{1,3}\), \(x_{1,4}\), \(x_{1,5}\), \(x_{1,6}\), \(x_{2,2}\), \(x_{2,3}\), \(x_{2,4}\), \(x_{2,5}\), and \(x_{2,6}\). The cost coefficients can be calculated as: \[c_{i,j} = \sum_{k=i}^j \mathit{count}_k \>\mathit{size}_j^2 \>\>\>\>\forall i\le j\] or if you prefer \[c_{i,j} = \mathit{size}_j^2 \sum_{i\le k\le j} \mathit{count}_k \ \>\>\>\>\forall i\le j\] This is like a set covering or better set partitioning problem (we want to cover exactly once: this is a set partitioning construct).
This leads to a large, but easy to solve MIP model: for \(T=4\), I see:
MODEL STATISTICS BLOCKS OF EQUATIONS 3 SINGLE EQUATIONS 386 BLOCKS OF VARIABLES 2 SINGLE VARIABLES 73,921 NON ZERO ELEMENTS 9,658,881 DISCRETE VARIABLES 73,920
This looks scary, but actually solves very fast:
The results look like:
This means we put items 1 through 155 in the smallest box with size 388 (area = \(388^2\)), etc.
When we run the model with \(T=3\) we see:
Root relaxation solution time = 6.73 sec. (3375.50 ticks) Nodes Cuts/ Node Left Objective IInf Best Integer Best Bound ItCnt Gap * 0+ 0 7.96958e+08 0.0000 100.00% Found incumbent of value 7.9695838e+08 after 102.45 sec. (46615.58 ticks) * 0 0 integral 0 3.29199e+08 3.29199e+08 2111 0.00% Elapsed time = 102.56 sec. (46669.97 ticks, tree = 0.00 MB, solutions = 2) Found incumbent of value 3.2919912e+08 after 102.56 sec. (46669.97 ticks)
The results look like:
---- 447 PARAMETER results count minsize maxsize area sum area i1 .i155 549.000 156.000 388.000 150544.000 8.264866E+7 i156 .i268 377.000 389.000 550.000 302500.000 1.140425E+8 i269 .i351 187.000 552.000 705.000 497025.000 9.294368E+7 i352 .i384 53.000 710.000 864.000 746496.000 3.956429E+7 total. 1166.000 3.291991E+8
This means we put items 1 through 155 in the smallest box with size 388 (area = \(388^2\)), etc.
When we run the model with \(T=3\) we see:
---- 447 PARAMETER results count minsize maxsize area sum area i1 .i155 549.000 156.000 388.000 150544.000 8.264866E+7 i156 .i284 423.000 389.000 574.000 329476.000 1.393683E+8 i285 .i384 194.000 576.000 864.000 746496.000 1.448202E+8 total. 1166.000 3.668372E+8
Indeed the total cost (area) goes up. Interestingly the smallest box size stays the same.
GAMS implementation
set i /i1*i384/; alias(i,j,k); set ij(i,j) 'allowed i,j combinations: i<=j' ijk(i,j,k) 'allowed i,j,k combinations: i<=k<=j' ; ij(i,j) = ord(i)<=ord(j); ijk(ij(i,j),k) = ord(k)>=ord(i) and ord(k)<=ord(j); table data(i,*) size count i1 156 1 i2 162 1 i3 168 1 i4 178 2
. . .
i381 823 1 i382 827 2 i383 855 2 i384 864 1 ; parameter count(i), size(i); count(i) = data(i,'count'); size(i) = data(i,'size'); scalar T 'number of different box sizes' /4/; binary variables x(i,j) 'items i-j in a single box type'; variable totalarea; parameter c(i,j) 'cost when items i-j are in box with size size(j)'; c(ij(i,j)) = sum(ijk(ij,k), count(k)*sqr(size(j))); equations cover(k) 'cover each item k exactly once' numboxes 'T different box sizes' objective 'minimize total area' ; cover(k).. sum(ijk(ij,k),x(ij)) =e= 1; numboxes.. sum(ij,x(ij)) =e= T; objective.. totalarea =e= sum(ij, c(ij)*x(ij)); model m /all/; option optcr=0; solve m minimizing totalarea using mip; set xij(i,j) 'selected x(i,j)'; xij(i,j) = x.l(i,j) > 0.5; parameter results(*,*,*); results(xij(i,j),'minsize') = size(i); results(xij(i,j),'maxsize') = size(j); results(xij(i,j),'area') = sqr(size(j)); results(xij,'count') = sum(ijk(xij,k),count(k)); results(xij,'sum area') = c(xij); results('total','','sum area') = totalarea.l; results('total','','count') = sum(ijk(xij,k),count(k)); display results; |
Notes:
- Intermediate sets are used to simplify things. I use this approach a lot. Sets are easier to debug than equations.
- Reporting is important. I try to collect meaningful information in the 3d parameter results. Hopefully the results can be interpreted even when not knowing the model or even when not knowing GAMS.
- The set xij(i,j) will indicate where we have x.l(i,j)=1. In practice, values for a binary variable can be 0.99999 or 1.00001. So I don't test against 1.0 exactly.
- I left out the data step where I combine duplicate item sizes. That was done in a separate piece of GAMS code.
Network model I
This problem can also be modeled as a network problem. See [2] for more details.
The network is not very simple. Consider again the 6 item, \(T=3\) example. We drew a picture of a feasible covering earlier. The same feasible solution for the network of this problem looks like:
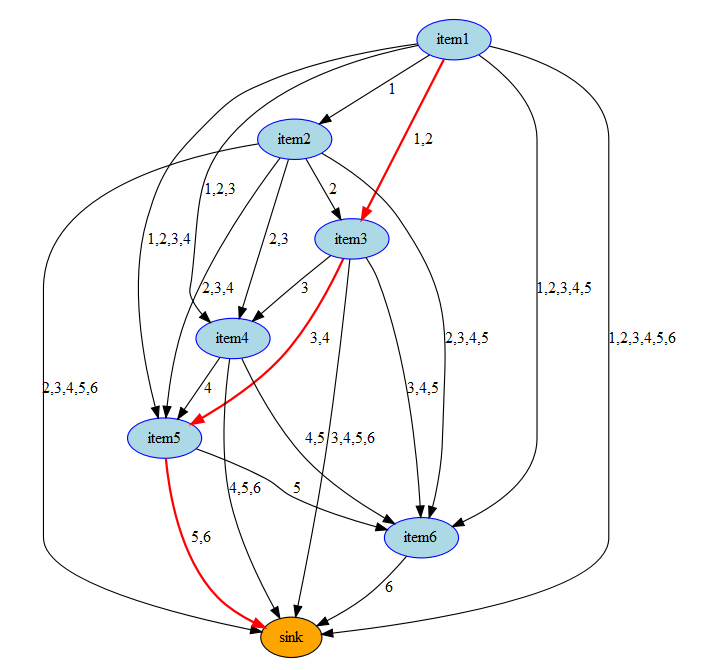 |
| Feasible solution for T=3 |
Selecting a link from item \(i\) to item \(j\) means: put items \(i,i+1,\dots,j-1\) into a box with size \(j-1\). Similarly, a link from item \(i\) to the sink node means: put items \(i,i+1,\dots,n\) into a box with size \(n\) (where \(n\) is the largest item or box).
The cost coefficients are defined by: \[\begin{align}c_{i,j} &= \mathit{size}_{j-1}^2 \sum_{k=i}^{j-1} \mathit{count}_k & \forall i\le j\\c_{i,\mathit{sink}} &= \mathit{size}_n^2 \sum_{k=i}^n \mathit{count}_k & \forall i \end{align}\]
We want to solve a shortest path problem from item 1 to the sink node with a side constraint: the number of "blue" nodes we visit should be exactly \(T\). The side constraint makes this a cardinality constrained or hop constrained shortest path problem. We can solve this as an MIP problem: \[\bbox[lightcyan,10px,border:3px solid darkblue] {\begin{align}min & \sum_{(i,j)\in A} c_{i,j} x_{i,j} \\ & \sum_{(j,i)\in A} x_{j,i} + b_i = y_i & \forall i & \>\> \text{(flow balance)}\\ & y_i = \sum_{(i,j)\in A} x_{i,j} & \forall i & \>\>\text{(outflow node $i$)}\\ &\sum_{i \ne \mathit{sink}} y_i = T &&\text{(cardinality)}\\ & x_{i,j},y_i \ge 0 \end{align} }\] Here \(b_i\) is the net exogenous supply of node \(i\). I.e. \[b_i = \begin{cases} 1 & \>\> \text{if $i=1$}\\ -1 & \>\> \text{if $i=\mathit{sink}$}\\ 0 & \>\>\text{otherwise}\end{cases}\]
---- 470 VARIABLE cost.L = 3.291991E+8 ---- 470 VARIABLE x.L arcs i156 i269 i352 sink i1 1.000 i156 1.000 i269 1.000 i352 1.000
This means our optimal grouping is \(i_1 - i_{155}\), \(i_{156} - i_{268}\), \(i_{269} - i_{351}\), \(i_{352} - i_{384}\). This is the same solution as for our set partitioning model.
GAMS Code
The GAMS code for this model can look like:
$ontext
Select Boxes Cardinality constrained shortest path $offtext sets iext 'orig nodes + sink' /i1*i384,sink/ i(iext) 'orig nodes w/o sink' /i1*i384/ ; table data(i,*) size count i1 156 1 i2 162 1 i3 168 1 i4 178 2 . . . i381 823 1 i382 827 2 i383 855 2 i384 864 1 ; parameter count(i), size(i); count(i) = data(i,'count'); size(i) = data(i,'size'); scalar T 'number of different box sizes' /4/; alias(iext,jext); alias(i,j,k); sets ij(i,j) 'allowed i,j combinations: i<=j' ijk(i,j,k) 'allowed i,j,k combinations: i<=k<=j' ; singleton set lastj(j) 'last element of j'; ij(i,j) = ord(i)<=ord(j); ijk(ij(i,j),k) = ord(k)>=ord(i) and ord(k)<=ord(j); lastj(j) = ord(j)=card(j); * * network topology * set a(iext,iext) 'arcs'; a(ij) = yes; a(i,'sink') = yes; parameter c(iext,iext) 'cost coefficients'; c(a(i,j)) = sqr(size(j-1)) * sum(ijk(i,j-1,k),count(k)); c(i,'sink') = sqr(size(lastj)) * sum(ijk(i,lastj,k),count(k)); parameter pinflow(iext) 'source/sink' / sink -1 i1 1 /; binary variables x(iext,iext) 'arcs' y(iext) 'outflow of node' ; variables cost; equations nodbal 'node balance' calcoutflow 'calc y' numboxes 'we need an active node for box' obj 'objective' ; obj.. cost =e= sum(a,c(a)*x(a)); calcoutflow(iext).. y(iext) =e= sum(a(iext,jext),x(a)); nodbal(iext).. sum(a(jext,iext), x(a)) + pinflow(iext) =e= y(iext); numboxes.. sum(i,y(i)) =e= T; model m /all/; * for this data set we can solve as LP (to be safe solve as MIP) solve m minimizing cost using rmip; display cost.l, x.l; * check if close to integer solution abort$sum((iext,jext)$(abs[x.l(iext,jext)-round(x.l(iext,jext))]>1e-4),1) "non-integer solution: solve as MIP"; * * reporting * set xij(i,jext) 'items i..j to into same box'; xij(i,jext) = x.l(i,jext+1) > 0.5; parameter results(*,*,*); results(xij(i,j),'minsize') = size(i); results(xij(i,j),'maxsize') = size(j); results(xij(i,j),'area') = sqr(size(j)); results(xij(i,j),'count') = sum(ijk(i,j,k),count(k)); results(xij(i,j),'sum area') = sqr(size(j)) * sum(ijk(i,j,k),count(k)); results('total','','sum area') = cost.l; results('total','','count') = sum(ijk(xij(i,j),k),count(k)); display results; |
Network Model II
The previous model was a network model with a side constraint. We can create a pure network by augmenting the network. Basically we keep track of the number of different boxes by indexing the nodes by item number and layer number. This means we have a larger number of nodes. The network can look like:
 |
| Layered network |
The results for the original data set with \(T=4\) looks like:
---- 467 VARIABLE cost.L = 3.291991E+8 ---- 467 VARIABLE x.L arcs i156.layer2 i269.layer3 i352.layer4 sink.Lsink i1 .layer1 1.00 i156.layer2 1.00 i269.layer3 1.00 i352.layer4 1.00
Note again that this must be interpreted as follows: group items \(i_1 - i_{155}\), \(i_{156} - i_{268}\), \(i_{269} - i_{351}\), \(i_{352} - i_{384}\) in box sizes large enough to hold \(i_{155}\), \(i_{268}\), \(i_{351}\), \(i_{384}\) . This is the same solution as for our earlier models.
GAMS Model
$ontext
Select Boxes Shortest path in layered network $offtext sets iext 'orig nodes + sink' /i1*i384,sink/ i(iext) 'orig nodes w/o sink' /i1*i384/ Lext 'orig layers + sink' /layer1*layer4,Lsink/ L(Lext) 'lyaers w/o sink' /layer1*layer4/ ; table data(i,*) size count i1 156 1 i2 162 1 i3 168 1 i4 178 2 . . . i381 823 1 i382 827 2 i383 855 2 i384 864 1 ; parameter count(i), size(i); count(i) = data(i,'count'); size(i) = data(i,'size'); scalar T 'number of different box sizes'; T = card(L); alias(iext,jext); alias(i,j,k); alias(Lext,L1ext,L2ext); alias(L,L1,L2); sets ij(i,j) 'allowed i,j combinations: i<=j' ijk(i,j,k) 'allowed i,j,k combinations: i<=k<=j' ; singleton sets lastj(j) 'last element of j' lastL(L) 'last element of L' ; ij(i,j) = ord(i)<=ord(j); ijk(ij(i,j),k) = ord(k)>=ord(i) and ord(k)<=ord(j); lastj(j) = ord(j)=card(j); lastL(L) = ord(L)=card(L); * * network topology * set a(iext,L1ext,jext,L2ext) 'arcs'; a(i,L1,j,L1+1) = ord(j)>ord(i); a(i,lastL,'sink','Lsink') = yes; parameter c(iext,L1ext,jext,L2ext) 'cost coefficients'; c(a(i,L1,j,L2)) = sqr(size(j-1)) * sum(ijk(i,j-1,k),count(k)); c(i,lastL,'sink','Lsink') = sqr(size(lastj)) * sum(ijk(i,lastj,k),count(k)); parameter pinflow(iext,Lext) 'source/sink' / sink.Lsink -1 i1.layer1 1 /; binary variables x(iext,Lext,iext,Lext) 'arcs' ; variables cost; equations nodbal 'node balance' obj 'objective' ; obj.. cost =e= sum(a,c(a)*x(a)); nodbal(iext,L1ext).. sum(a(jext,L2ext,iext,L1ext), x(a)) + pinflow(iext,L1ext) =e= sum(a(iext,L1ext,jext,L2ext), x(a)); model m /all/; * this is a pure network: we can solve as an LP solve m minimizing cost using rmip; option x:2:2:2; display cost.l, x.l; * * reporting * set xij(i,jext) 'items i..j to into same box'; xij(i,jext) = sum((L1ext,L2ext),x.l(i,L1ext,jext+1,L2ext)) > 0.5; parameter results(*,*,*); results(xij(i,j),'minsize') = size(i); results(xij(i,j),'maxsize') = size(j); results(xij(i,j),'area') = sqr(size(j)); results(xij(i,j),'count') = sum(ijk(i,j,k),count(k)); results(xij(i,j),'sum area') = sqr(size(j)) * sum(ijk(i,j,k),count(k)); results('total','','sum area') = cost.l; results('total','','count') = sum(ijk(xij(i,j),k),count(k)); display results; |
As this is a pure network, we can ask Cplex to use the network simplex method to solve this. We see:
--- 1,537 rows 220,993 columns 662,977 non-zeroes --- 220,992 discrete-columns --- Executing CPLEX: elapsed 0:01:15.411 ... Tried aggregator 1 time. LP Presolve eliminated 393 rows and 219470 columns. Aggregator did 764 substitutions. Reduced LP has 380 rows, 759 columns, and 1138 nonzeros. Presolve time = 2.25 sec. (568.28 ticks) Extracted network with 381 nodes and 759 arcs. Extraction time = 0.00 sec. (0.11 ticks) Iteration log . . . Iteration: 0 Infeasibility = 1.000000 (24337) Iteration: 100 Infeasibility = 1.000000 (24337) Iteration: 200 Infeasibility = 1.000000 (24337) Network - Optimal: Objective = 3.2919911900e+08 Network time = 0.00 sec. (0.07 ticks) Iterations = 261 (261) LP status(1): optimal Cplex Time: 2.39sec (det. 588.24 ticks)
We see the presolver takes most of the time, but is also highly effective. The presolved model takes zero seconds to solve.
Dynamic Programming
A dynamic programming algorithm is an alternative for this problem. If we define \[f_{i,b} = \text{minimum total area when we pack items $1,\dots,i$ (ordered and with unique size) in $b$ box sizes}\] then we can write down the recursion:\[ f_{i,b} = \min_{k=b-1,\dots,i-1} \left\{ f_{k,b-1} + \mathit{size}_i^2 \sum_{j=k+1}^i \mathit{count}_j \right\}\]
When we code this up in R we could see something like:
data <- c( 156,162,168,178,178,180,185,185,190,192,193,194,195,195,197,197,198,198,199,200,202,206, 206,210,210,210,212,212,214,215,217,217,217,217,217,218,220,220,220,220,220,220,220,220, ... 727,730,733,733,734,734,734,735,735,735,738,740,743,744,754,755,755,755,755,755,758,760, 766,766,780,780,780,780,780,780,780,782,783,785,795,805,806,820,823,827,827,855,855,864) t<-table(data) count <- as.vector(t) size <- as.numeric(rownames(t)) cumulative <- cumsum(count) # number of box sizes, number of item sizes NB <- 4 NI <- length(size) # allocate matrix NI rows, NB columns (initialize with NAs) # f[ni,nb] = cost when we have ni items and nb blocks F <- matrix(NA,NI,NB) S <- matrix("",NI,NB) # initialize for nb=1 F[1:NI,1] <- cumulative * size[1:NI]^2 S[1:NI,1] <- paste("(",1,"-",1:NI,")",sep="") # dyn programming loop for (nb in 2:NB) { for (ni in nb:NI) { k <- (nb-1):(ni-1) v <- F[k,nb-1] + (cumulative[ni]-cumulative[k])*size[ni]^2 F[ni,nb] <- min(v) # create path (string) mink <- which.min(v) + nb - 2 s <- paste("(",mink+1,"-",ni,")",sep="") S[ni,nb] <- paste(S[mink,nb-1],s,sep=",") } } for (nb in 1:NB) { cat(sprintf("%s boxes: %s, total area = %g\n",nb,S[NI,nb],F[NI,nb])) }
Note that the inner \(k\) loop is vectorized. The results look like:
1 boxes: (1-384), total area = 8.70414e+08 2 boxes: (1-268),(269-384), total area = 4.59274e+08 3 boxes: (1-155),(156-284),(285-384), total area = 3.66837e+08 4 boxes: (1-155),(156-268),(269-351),(352-384), total area = 3.29199e+08
The results for 1,2 and 3 boxes we get for free.
Data
The data set used here is shown below:
156,162,168,178,178,180,185,185,190,192,193,194,195,195,197,197,198,198,199,200,202,206 206,210,210,210,212,212,214,215,217,217,217,217,217,218,220,220,220,220,220,220,220,220 220,220,222,223,223,224,225,225,225,225,225,225,225,226,226,226,227,228,228,228,228,230 230,230,230,230,230,230,230,230,230,230,230,230,232,232,232,233,233,234,234,235,235,235 235,238,238,238,238,240,240,240,240,240,240,240,240,240,241,242,242,242,242,243,244,244 244,245,246,247,247,247,249,250,250,250,250,250,251,252,252,252,252,253,254,254,254,255 255,255,255,255,256,256,257,257,257,258,258,258,258,258,259,260,260,260,260,260,260,260 260,260,262,262,262,262,262,262,262,264,264,264,265,265,265,265,265,266,267,267,267,267 268,268,268,268,268,268,269,270,270,270,270,270,270,270,270,270,270,271,272,272,272,272 272,273,273,273,273,274,274,274,274,274,275,275,275,275,275,275,277,277,277,278,278,278 278,278,278,280,280,280,280,281,282,282,284,285,285,285,285,285,285,287,287,287,288,288 288,288,288,289,290,290,290,290,290,290,290,290,290,290,290,292,292,293,293,294,294,294 295,295,295,295,295,295,295,295,296,296,297,297,298,298,298,298,300,300,300,300,300,300 300,300,300,300,300,300,300,300,302,302,303,303,303,303,304,305,305,305,305,305,306,306 307,308,308,308,310,310,310,310,310,310,310,312,312,312,312,313,315,315,315,315,315,315 315,315,315,317,317,317,317,318,318,318,318,320,320,320,320,320,320,320,320,320,320,320 320,320,322,323,323,325,325,325,325,326,326,327,327,328,328,330,330,330,330,330,330,330 332,333,333,334,334,334,334,335,335,335,335,335,336,336,336,338,338,339,339,340,340,340 340,340,340,340,342,342,342,342,343,345,345,345,345,345,345,345,346,346,346,347,347,348 348,348,349,350,350,350,350,350,350,350,350,350,350,350,350,350,350,350,350,350,350,352 352,353,353,353,353,354,354,354,356,357,357,357,357,358,358,360,360,360,360,360,360,360 360,360,360,360,360,361,362,362,362,363,363,364,364,364,364,365,365,365,365,365,365,365 367,367,367,368,370,370,370,370,370,370,370,370,370,372,372,372,373,375,375,375,375,375 375,377,377,377,378,380,380,380,380,380,380,380,380,380,380,380,380,381,382,383,383,383 383,384,384,384,384,385,385,385,386,386,386,386,387,387,387,387,388,388,388,388,388,389 390,392,392,393,394,394,395,396,397,397,398,398,398,400,400,400,400,400,400,400,400,405 405,408,410,410,410,410,410,410,412,412,412,412,412,413,415,415,416,416,417,417,418,418 419,419,419,420,420,420,420,420,420,420,420,423,423,423,423,424,424,425,425,425,428,428 430,430,430,430,430,430,430,430,430,430,430,430,431,432,432,432,432,433,433,433,433,433 434,434,435,435,435,435,437,438,438,438,438,440,440,440,440,440,440,440,441,442,443,444 444,445,445,445,445,445,445,445,445,446,447,448,448,450,450,450,450,450,450,450,450,450 452,453,453,455,455,455,455,456,457,458,458,458,458,459,460,460,460,460,460,460,460,462 462,463,464,465,465,465,465,465,465,465,466,466,467,467,467,467,467,468,468,468,469,469 470,470,470,470,470,470,470,470,470,472,472,472,474,475,475,476,478,478,478,478,480,480 480,480,480,480,480,480,480,480,480,480,482,482,482,482,482,482,482,485,485,485,485,488 488,488,488,490,490,490,490,490,490,490,490,491,491,492,492,492,492,492,492,492,493,493 495,495,495,496,497,498,498,498,498,498,498,498,499,500,500,500,500,500,500,502,502,502 505,505,505,505,505,506,507,507,510,510,510,510,510,510,510,510,510,510,510,510,512,512 513,514,515,515,517,517,518,520,520,520,520,520,520,522,523,523,523,524,525,525,525,525 525,525,528,528,528,528,528,528,528,530,530,530,530,530,530,531,532,534,535,535,535,535 535,536,538,538,538,539,540,540,540,540,540,540,540,540,540,540,540,541,543,543,543,544 544,545,545,545,546,546,546,547,547,548,548,550,550,550,550,550,550,550,550,550,550,550 550,550,552,552,555,555,555,555,555,555,555,557,557,557,557,560,560,560,560,560,562,562 563,563,564,565,565,565,565,565,565,567,567,568,568,569,569,569,570,570,570,571,572,572 573,574,574,574,576,576,578,580,580,580,584,585,585,587,588,590,592,593,596,597,600,600 600,600,602,602,602,602,602,603,604,605,605,605,605,605,605,605,607,607,607,608,610,610 610,610,610,610,612,612,612,612,615,615,615,615,618,618,620,622,624,625,625,625,627,627 628,628,628,630,630,632,633,635,635,637,638,638,640,640,640,640,640,642,643,647,648,649 650,650,655,655,655,656,660,660,660,660,660,662,662,663,664,664,664,664,665,665,665,670 670,672,677,677,679,680,680,680,680,680,685,685,687,688,690,690,692,694,695,697,698,700 700,701,704,704,705,705,705,705,705,705,705,705,705,710,710,712,715,717,720,720,722,723 727,730,733,733,734,734,734,735,735,735,738,740,743,744,754,755,755,755,755,755,758,760 766,766,780,780,780,780,780,780,780,782,783,785,795,805,806,820,823,827,827,855,855,864
References
- Need to create 3−4 different box sizes and to minimize material waste for a set of n objects that need to fit into these boxes, https://math.stackexchange.com/questions/2843990/need-to-create-3-4-different-box-sizes-and-to-minimize-material-waste-for-a-se/2850260
- On the scheduling of reading book chapters, https://yetanothermathprogrammingconsultant.blogspot.com/2018/02/on-scheduling-of-reading-book-chapters.html
No comments:
Post a Comment