Numberlink Models

In the Numberlink puzzle [1] we need to connect end-points by paths over a board with cells such that:

1. Each cell is part of a path
2. Paths do not cross

E.g. the puzzle on the left has a solution as depicted on the right [1]:

 

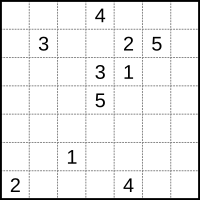
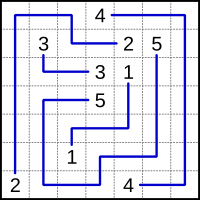
The picture on the left provides the end-points. The solution in the picture on the right can be interpreted as:

The main variable we use is:

\[x_{p,k} = \begin{cases}1 & \text{ if cell $p$ has value $k$}\\                                        0 & \text{ otherwise}\end{cases}\]

The main thought behind solving this model as a math programming model is to look at the neighbors of a cell. The neighbors are the cells immediately on the left, on the right, below or above. If a cell is an end-point of a path then it has exactly one neighbor with the same value. If a cell is not an end-point it is on a path between end-points and has two neighboring cells with the same value.

This leads to the following high-level MIQCP (Mixed Integer Quadratically Constrained Model):

\[\bbox[lightcyan,10px,border:3px solid darkblue] {\begin{align}                       &\sum_k x_{p,k} = 1\\                       &\sum_{q|N(p,q)} \sum_k x_{p,k}\cdot x_{q,k} =\begin{cases} 1&\text{if cell $p$ is an end-point}\\ 2&\text{otherwise}\end{cases}\\ &x_{p,k} = c_{p,k} \>\>\> \text{if cell $p$ is an end-point}\\&x_{p,k}\in \{0,1\}\end{align}}\]

Here \(N(p,q)\) is true if \(p\) and \(q\) are neighbors and \(c_{p,k}\) indicates if cell \(p\) is an end-point with value \(k\). The model has no objective: we are just looking for a feasible integer solution. Unfortunately, this is a non-convex model. The global solver Baron can solve this during its initial local search heuristic phase:

Doing local search   Solving bounding LP   Starting multi-start local search   Done with local search ===========================================================================     Iteration    Open nodes         Time (s)    Lower bound      Upper bound   *         1             0            23.09      0.00000          0.00000                1             0            23.11      0.00000          0.00000      Cleaning up                          *** Normal completion ***              Wall clock time:                    23.73   Total CPU time used:                23.12   Total no. of BaR iterations:       1   Best solution found at node:       1   Max. no. of nodes in memory:       1   All done

Of course we can try to linearize this model so it becomes a MIP model (and thus convex). The product of two binary variables \(y=x_1\cdot x_2\) can be linearized by:

\[\begin{align} &y \le x_1\\ &y\le x_2\\ &y \ge x_1+x_2-1\\ &y \in \{0,1\}\end{align}\]

We can relax \(y\) to a continuous variable between 0 and 1. In our model we can exploit some symmetry. This reduces the number of variables and equations:

\[\begin{align} &y_{p,q,k} \le x_{p,k}&\forall p<q\\ &y_{p,q,k} \le x_{p,k}&\forall p<q\\ &y_{p,q,k} \ge x_{p,k}+x_{q,k}-1&\forall p<q\\ &y_{p,q,k} \in \{0,1\}&\forall p<q\end{align}\]

The non-linear counting equation can now be written as:

\[\sum_{q|N(p,q)}  \sum_k \left( y_{p,q,k}|p<q + y_{q,p,k}|q<p \right)= b_{p}\]

Here \(b_p\) is the right-hand side of the counting constraint. This solves very fast. Cplex shows:

Tried aggregator 2 times. MIP Presolve eliminated 6178 rows and 1840 columns. MIP Presolve modified 40 coefficients. Aggregator did 394 substitutions. Reduced MIP has 11167 rows, 3892 columns, and 26610 nonzeros. Reduced MIP has 3892 binaries, 0 generals, 0 SOSs, and 0 indicators. Presolve time = 0.19 sec. (42.60 ticks) Found incumbent of value 0.000000 after 0.36 sec. (79.41 ticks) Root node processing (before b&c):    Real time             =    0.36 sec. (79.70 ticks) Sequential b&c:    Real time             =    0.00 sec. (0.00 ticks)                            ------------ Total (root+branch&cut) =    0.36 sec. (79.70 ticks) MIP status(101): integer optimal solution Cplex Time: 0.36sec (det. 79.72 ticks)

Cplex solves this in the root node.

Unique solution

A well-formed puzzle has exactly one solution. We can check this by adding a constraint that forbids the solution we just found. After adding this cut the model should be infeasible. Let \(\alpha_{p,k} = x^*_{p,k}\) be our feasible solution. Then our cut can look like:

\[\sum_{p,k} \alpha_{p,k} x_{p,k} \le |P|-1\]

where \(|P|\) is the number of cells. Indeed, when we add this constraint, the model becomes infeasible. So, we can conclude this is a proper puzzle.

Alternative formulation

In the comments Rob Pratt suggests a formulation that works a better in practice. The counting constraint is replaced by:

\[\begin{align} &\sum_{q|N(p,q)} x_{q,k}=1 &&\text{if cell $p$ is an end-point with value $k$}\\ &2x_{p,k}\le \sum_{q|N(p,q)} x_{q,k} \le 2x_{p,k}+M_p(1-x_{p,k})&&\text{if cell $p$ is not an end-point} \end{align}\]

where \(M_p\) can be replaced by \(M_p=|N(p,q)|=\sum_{q|N(p,q)} 1\) (the number of neighbors of cell \(p\)). This is at most 4 so not really a big big-M.

This formulation seems to work better. We can solve with this something like:

This problem has also exactly one solution.

Historical note

In [3] an early version of this puzzle is mentioned, appearing in

Here the goal is to draw paths from each house to its gate without the paths overlapping [4].

Large problems

For larger problems MIP solvers are not the best tool. From notes in [2] it looks like SAT solvers are most suitable for this type problem. In a CP/SAT framework we could use directly an integer variable \(x_p \in \{1,\dots,K\}\), and write the counting constraints as something like:

\[\sum_{q|N(p,q)} 1|(x_p=x_q) = \begin{cases} 1&\text{if cell $p$ is an end-point}\\ 2&\text{otherwise}\end{cases}\]

References

1. Numberlink, https://en.wikipedia.org/wiki/Numberlink
2. Hakan Kjellerstrand, Numberlink puzzle in Picat, https://github.com/hakank/hakank/blob/master/picat/numberlink.pi (shows a formulation in the Picat language)
3. Aaron Adcock, Erik D. Demaine, Martin L. Demaine, Michael P. O'Brien, Felix Reidl, Fernando Sanchez Villaamil, and Blair D. Sullivan, Zig-Zag Numberlink is NP-Complete, 2014, https://arxiv.org/pdf/1410.5845.pdf
4. Facsimiles of The Brooklyn Daily Eagle,  http://bklyn.newspapers.com/image/50475607/, https://bklyn.newspapers.com/image/50475838/
5. Neng-Fa Zhou, Masato Tsuru, Eitaku Nobuyama, A Comparison of CP, IP, and SAT Solvers through a common interface, 2012, http://www.sci.brooklyn.cuny.edu/~zhou/papers/tai12.pdf