Simple piecewise linear problem, not so easy with binary variables

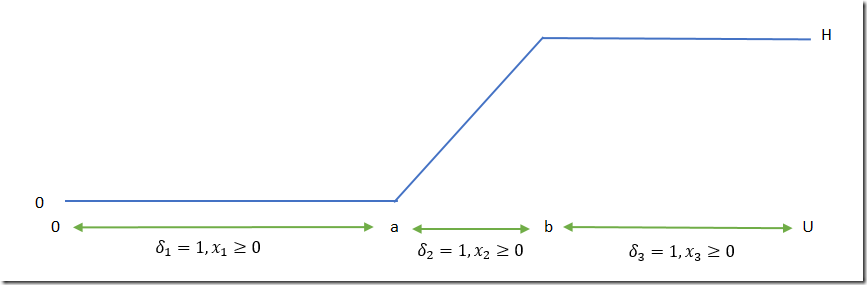
The following picture illustrates the problem:

The blue line is what we want to model:

$$\bbox[lightcyan,10px,border:3px solid darkblue]{    y = \begin{cases}     0 & \text{if $0 \le x \le a$}\\    (x-a)\displaystyle\frac{H}{b-a} & \text{if $a < x < b$}\\    H & \text{if $x\ge b$}\end{cases}}$$

Is there much we can exploit here, from this simple structure? I don’t believe so, and came up with:

$$\begin{align} &x_1 \le a \delta_1\\ &a \delta_2 \le x_2 \le b \delta_2\\ &b \delta_3 \le x_3 \le U \delta_3\\ &\delta_1+\delta_2+\delta_3 = 1\\ &x = x_1+x_2+x_3\\ &y = (x_2 - a \delta_2)\displaystyle\frac{H}{b-a} + H \delta_3 \\ &\delta_k \in \{0,1\}\\ &x_i \ge 0\\ &0 \le x \le U \end{align}$$

Update

Added missing $\sum_k \delta_k=1$, see comments below.