Assuming an \(n \times n\) board (with \(n\) even), we need to fill the cells \((i,j)\), with values 0 or 1, with the following restrictions:
- The number of ones in each row and in each column is equal to \(\displaystyle\frac{n}{2}\).
- Then we have also: The number of zeroes in each row and in each column is equal to \(\displaystyle\frac{n}{2}\).
- There can be no duplicate rows and no duplicate columns.
- In a row or column there cannot be more than two consecutive zeroes or ones.
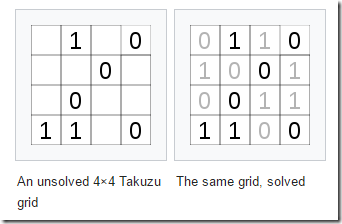
A small example is given in (1):
Of course our central variable will be \(x_{i,j}\in\{0,1\}\). Condition 1 can be easily modeled using two constraints:
| \[\begin{align} &\sum_j x_{i,j} = \frac{n}{2}\>\> \forall i\\ &\sum_i x_{i,j} = \frac{n}{2}\>\> \forall j \end{align}\] |
Condition 2 we don’t need to model explicitly: this follows from the above constraints.
Condition 3 (no duplicate rows or columns) is not very easy. One way to handle this, is to calculate a value for each row and column as follows:
| \[\begin{align} &v_i = \sum_j 2^{j-1} x_{i,j}\\ &w_j = \sum_i 2^{i-1} x_{i,j} \end{align}\] |
and then make sure there are no duplicate \(v_i\)’s or duplicate \(w_j\)’s. This can be done using some all-different formulation (3). A big-M approach to implement \(v_i \le v_{i’}-1 \textbf{ or } v_i \ge v_{i’}+1, \forall i\ne i’\) can look like:
| \[\begin{align} &v_i \le v_{i’}-1 + M \delta_{i,i’}\\ &v_i \ge v_{i’}+1 – M (1-\delta_{i,i’})\\ &\delta_{i,i’} \in \{0,1\} \end{align}\] |
However I want to attack this in a different way, using an xor condition (4). The constraints involved can be conceptualized as:
| \[\begin{align} &\sum_j |x_{i,j} – x_{i’,j}| \ge 1 \>\> \forall i\ne i’\\ &\sum_i |x_{i,j} – x_{i,j’}| \ge 1 \>\> \forall j\ne j’ \end{align}\] |
The value \(z_{i,j,i’,j’}=|x_{i,j}-x_{i’,j’}|\) can be interpreted as \(z_{i,j,i’,j’}=x_{i,j} \textbf{ xor } x_{i’,j’}\): zero if \(x_{i,j}\) and \(x_{i’,j’}\) are identical and one if they are different. This in turn can be written as a set of inequalities (4):
| \[\begin{align} &z_{i,j,i’,j’}\le x_{i,j} + x_{i’,j’}\\ &z_{i,j,i’,j’}\ge x_{i,j} - x_{i’,j’}\\ &z_{i,j,i’,j’}\ge x_{i’,j’} - x_{i,j}\\ &z_{i,j,i’,j’}\le 2 - x_{i,j} - x_{i’,j’}\\ &z_{i,j,i’,j’} \in \{0,1\} \end{align}\] |
After this we just need:
| \[\begin{align} &\sum_j z_{i,j,i’,j} \ge 1 \>\> \forall i\ne i’\\ &\sum_i z_{i,j,i,j’} \ge 1 \>\> \forall j\ne j’ \end{align}\] |
Due to the nature of these conditions on \(z\) we can limit the xor constraints to
| \[\begin{align} &z_{i,j,i’,j’}\le x_{i,j} + x_{i’,j’}\\ &z_{i,j,i’,j’}\le 2 - x_{i,j} - x_{i’,j’}\\ &z_{i,j,i’,j’} \in \{0,1\} \end{align}\] |
Note that we do not need to compute all \(z\) for all combinations \((i,j)\), \((i’,j’)\) (e.g. we never compare \(x_{2,3}\) with \(x_{3,2}\)). Furthermore we can relax \(z\) to be continuous between zero and one. Also note that if we compared row \(i\) and \(i’\) then we don’t need to compare row \(i’\) and row \(i\). Similarly for the columns. So we can do:
| \[\begin{align} &\sum_j z_{i,j,i’,j} \ge 1 \>\> \forall i< i’\\ &\sum_i z_{i,j,i,j’} \ge 1 \>\> \forall j< j’ \end{align}\] |
Finally we need to handle restriction 4. This can be implemented as:
| \[\begin{align} &1\le x_{i,j}+x_{i,j+1}+x_{i,j+2}\le 2\\ &1\le x_{i,j}+x_{i+1,j}+x_{i+2,j}\le 2 \end{align}\] |
Usually we need to write this as four inequalities (unless we can specify ranged equations). If the summation was longer I would have introduced extra variables with bounds one and two to reduce the number of constraints.
Note that the lower bound of one can also be inferred from \((1-x_{i,j})+(1-x_{i,j+1})+(1-x_{i,j+2})\le 2 \Rightarrow x_{i,j}+x_{i+1,j}+x_{i+2,j} \ge 1\).
Complete model
The variables are:
The dummy variable is related to a dummy objective: we look for a feasible integer solution only.
The different \(z\) values we need to compare is encoded in a set compare:
Finally the model equations are:
The result looks like:
| ---- 77 VARIABLE x.L i1 i2 i3 i4 i1 1 1 |
A large problem
The site (2) contains some “very hard” 14 x 14 puzzles. An example is:
It is interesting to see how this model behaves on this problem. It turns out the problem can be solved completely in preprocessing. E.g. Cplex and Gurobi report that zero Simplex iterations were needed and solve this problem blazingly fast:
| Tried aggregator 3 times. Root node processing (before b&c): |
Verifying Uniqueness
A well-formed puzzle has only one solution. To verify whether a solution is unique we can use a similar strategy as in (6):
- First solve the model to obtain a solution \(x^*_{i,j}\).
- Formulate a constraint to forbid this solution.
- Add this constraint to the model and resolve. The solver should not find a new solution but rather report that this model is infeasible.
Here the cut can be formulated as:
| \[\sum_{i,j} x^*_{i,j} x_{i,j} \le \frac{n^2}{2}-1\] |
Data Entry
Entering the problem data:
is an interesting issue. In GAMS “zero” and “does not exist” is identical, so we can not just use:
table init(i,j)
i1 i2 i3 i4
i1 1 0
i2 0
i3 0
i4 1 1 0
;
I used the following, which is not very clean:
table init(i,j)
i1 i2 i3 i4
i1 1 2
i2 2
i3 2
i4 1 1 2
;
x.fx(i,j)$(init(i,j)=1) = 1;
x.fx(i,j)$(init(i,j)=2) = 0;
Not sure if this is better:
parameter init(i,j) / #i.#j NA /;
$onmulti
table init(i,j)
i1 i2 i3 i4
i1 1 0
i2 0
i3 0
i4 1 1 0
;
variable x(i,j);
x.fx(i,j)$(init(i,j)<>NA) = init(i,j);
Note that AMPL has a "default" facility, so we can use in a data file:
param init default -1 : i1 i2 i3 i4 :=
i1 . 1 . 0
i2 . . 0 .
i3 . 0 . .
i4 1 1 . 0
;
It makes sense to use Excel for data entry. The initial configuration in Excel can look like:
To read this into GAMS and retain the zeros we can use the following code:
parameter init(i,j);
$call 'gdxxrw i=takuzu.xlsx sq=n par=init rng=b3 rdim=1 cdim=1'
$oneps
$gdxin takuzu.gdx
$loaddc init
display init;
The Squeeze=no option in the call to GDXXRW will tell it to retain the zeros. The $OnEps command tells GAMS to read the zero as an EPS special value. EPS is very useful: it is physically stored in the sparse data structures, but as soon as you do a numerical operation on it, it becomes zero. This will show:
| ---- 12 PARAMETER init i1 i2 i3 i4 i1 1.000 EPS |
This will now allow us to fix variables as:
binary variable x(i,j);
x.fx(i,j)$init(i,j) = init(i,j);
This model turned out to have quite a few interesting angles.
References
- Takuzu, https://en.wikipedia.org/wiki/Takuzu
- Online Takuzu puzzles, http://www.binarypuzzle.com/
- All-different and Mixed Integer Programming, http://yetanothermathprogrammingconsultant.blogspot.com/2016/05/all-different-and-mixed-integer.html
- xor as Inequalities, http://yetanothermathprogrammingconsultant.blogspot.com/2016/02/xor-as-linear-inequalities.html
- Similar puzzles are Sudoku and KenKen: http://yetanothermathprogrammingconsultant.blogspot.com/2016/10/mip-modeling-from-sudoku-to-kenken.html
- Unique Solutions in KenKen, http://yetanothermathprogrammingconsultant.blogspot.com/2016/12/unique-solutions-in-kenken.html





No comments:
Post a Comment