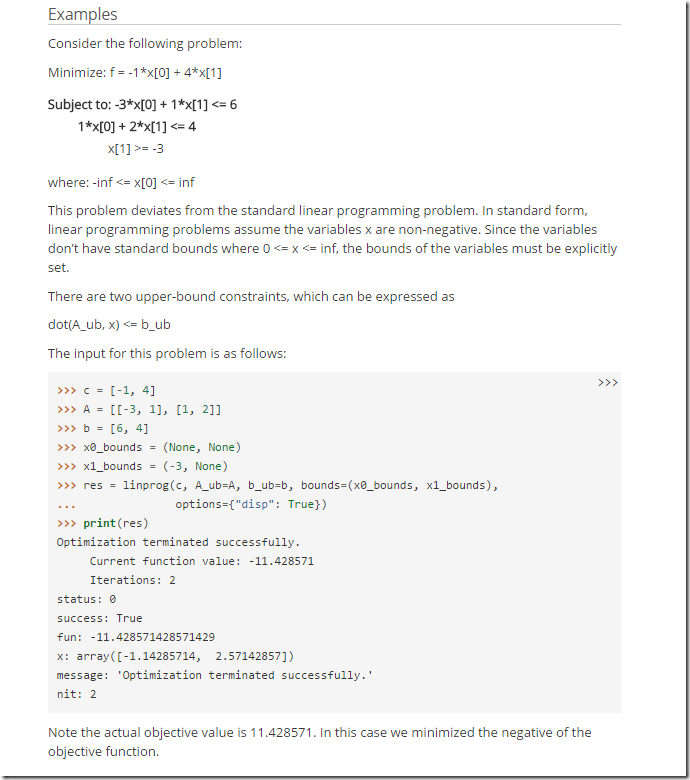
Source. In (1) and (2) an interesting problem is described: the aircraft landing problem. We have an airport with m runways, where we want to schedule aircrafts to land. Each aircraft has a target landing time and some allowed time window (it can land a bit earlier or somewhat later; typically the window is not symmetric around the target landing time). There is a required time between two landings (separation time) depending on the type of aircraft and the assigned runway. If two planes are scheduled on the same runway the separation time is longer than if they land on different runways.
The MIP model shown in (2) is as follows:
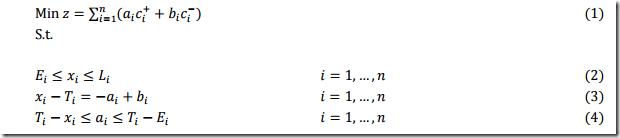
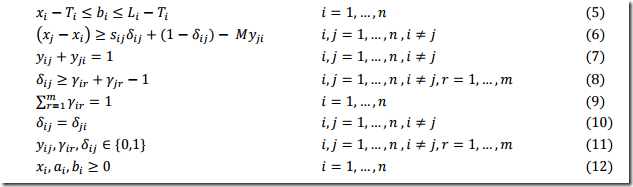
As usual I have some comments on the equations. Below I discuss each equations in turn (the numbers correspond to the equation number).
- The objective shows we have different costs for landing before or after the target landing time.
- This equation is just really a set of bounds that form the time-window. Usually I write these explicitly as bounds instead of constraints, even if presolvers will typically do this for you. When I specify them as bounds, I just want to convey in the model I know these restrictions are just bounds and paid attention.
- This constraint looks a bit unfamiliar, but actually is just a variable splitting constraint. Only one of \(a_i\), \(b_i\) will be nonzero due to the objective (if both are nonzero the LP solution of the current relaxation is not optimal).
- This constraint puts some limits on \(a_i\), but does not look like we need it. The first part: \(a_i \ge T_i-x_i\) follows from (3) while the bound \(a_i\le T_i-E_i\) follows from (2).
- This is similar and also looks redundant to me.
- This is a main constraint in the model. It says: if aircraft \(j\) is after \(i\) then there should be 1 or \(s_{i,j}\) minutes in between, depending on whether they land at the same runway. This equation gives rise to the thought we can make use of symmetry in the variables \(\delta_{i,j}\) (landing on same runway) and \(y_{i,j}\) (ordering). We know that \(\delta_{j,i} = \delta_{i,j}\) and that \(y_{j,i} = 1-y_{i,j}\). So we can save on these variables by exploiting that. Let’s say that we only have \(\delta_{i,j}\) and \(y_{i,j}\) for \(i<j\) (i.e. both are strictly upper triangular matrices) then we need to split constraint (6) into two parts:
\[\begin{align} x_j-x_i & \ge s_{i,j} \delta_{i,j} + (1 – \delta_{i,j}) – M(1-y_{i,j}) \>\> & \forall i<j \\
x_j-x_i & \ge s_{i,j} \delta_{j,i} + (1 – \delta_{j,i}) – M y_{j,i} \>\> & \forall i>j \end{align}\]
I am not sure if presolvers are so smart they can do this also. Even if they did, I would prefer to add this logic myself to show I have thought about this. We could do the same thing for \(s_{i,j}\) as the data seems to indicate \(s_{i,j}\) is symmetric. Saving on binary variables is more important that saving a few bytes on data, so we skip that. In addition, in practice \(s_{i,j}\) may not be symmetric (consider a Cessna before or after an A380).
Of course we need to use a good value for \(M\) that is as small as possible. Probably we should use \(M_{i,j}\) instead (i.e. use several constants). Finally we note that if for a combination \(i,j\) the time windows are far away from each other we can even drop this equation altogether. I ignore this for now because the data sets I am looking at now do not have such combinations. - We can drop this constraint if we only consider \(y_{i,j}\) for \(i<j\). Of course we need to be careful when we use \(y_{i,j}\) in the model (see the discussion of the previous constraint).
- This constraint can be considered as a linearization of \(\delta_{i,j}=\max_r \gamma_{i,r}\gamma_{j,r}\). This is a multiplication of two binary variables. We can get rid of the max and linearize by
\[ \delta_{i,j} \ge \gamma_{i,r}+\gamma_{j,r}-1\>\> \forall r, i\ne j \]
Note that we let \(\delta_{i,j}\) float when aircraft \(i\) and \(j\) do not share a runway. The objective will drive it to zero when needed. Forcing \(\delta_{i,j}=0\) in that case is not so easy: we would need some intermediate variables for that.
When we exploit symmetry we can reduce the number of constraints for equation (8). In our case it would become
\[\delta_{i,j}\ge \gamma_{i,r} + \gamma_{j,r}-1 \>\> \forall r, i<j\] - Each aircraft has to land on exactly one runway.
- This equation can be deleted when we exploit symmetry ourselves. Note that the given domain: \(i,j=1,..,n, i\ne j\) for this equation seems a bit generous. I guess they mean \(i<j\).
- Here I would note that I would restrict the domains of \(\delta_{i,j}\) and \(y_{i,j}\) to \(i<j\).
- When using a variable splitting technique I usually do not create two variables with different names (like \(a_i\) and \(b_i\)) but would rather create a single variable \(d_{i,k}\) (‘d’ for deviation from target landing time), where \(k=\{\text{early},\text{late}\}\). This is largely a matter of taste.
In summary, here is my version of the model:
The performance of the new formulation looks good at least on one small data set using 2 runways:
Some of the larger problems (n=44,n=50) are actually even easier to solve.
I am not sure how to depict the solution. Here is an attempt:
The dots indicate when a landing is scheduled and on which runway.
Conclusion
As usual: there is always a lot to think about, even for a small model like this.
References
(1) J. E. BEASLEY e.a., “Scheduling Aircraft Landings— The Static Case”, Transportation Science,Vol. 34, No. 2, May 2000
(2) Amir Salehipour, “Solving Large Aircraft Landing Problems on Multiple Runways by Applying a Constraint Programming Approach”, Report, The University of Newcastle, Australia, 2016
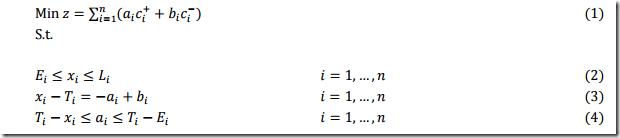
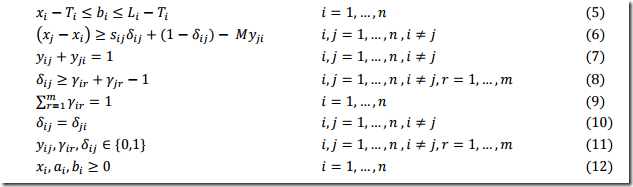
![image_thumb[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjF2NNRP-rmou9JlLd86PCc5OOIgr4hL9Rtxg0kRHPU1gWTDgTeyPF-D62Wee_-5IdIprN3y9MZ9DoTffqKQHT0OFc2xPHY88wPOc045FlQIybfzYO2snCaA_RZ79_VhNI2mMUbuH1fNtfh/s1600-h/image_thumb%25255B1%25255D%25255B4%25255D.png "image_thumb[1]")
