How do they make a bug like this?

For a small project I needed to solve a very small QP model. As the input and output were in Excel, it made some sense to try Excel’s Solver. One of the constraints is:

The way to do this is to create a cell with the sum and then use Solver.SolverAdd to add a constraint. The complete call can look like:

Call Solver.SolverAdd(CellRef:=sumcell, Relation:=2, FormulaText:=1)

See http://msdn.microsoft.com/en-us/library/office/ff838657(v=office.14).aspx

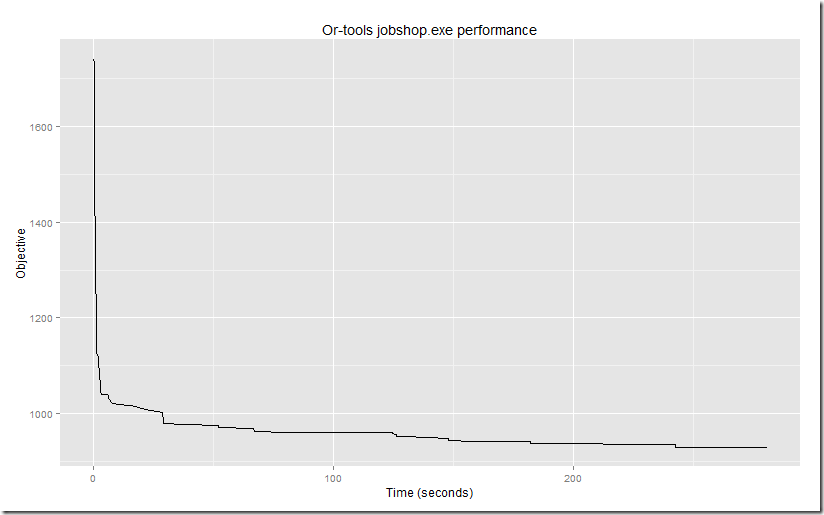
Unfortunately (for me) this did not work and I see:

After much experimentation I used instead:

Call Solver.SolverAdd(CellRef:=sumcell, Relation:=2, FormulaText:=0.999999999999999)

Now I see:

How in the world can such a bug be introduced? Some bugs make sense, but the logic of this one is difficult to fathom. I cannot but think there must be a statement somewhere:

if rhs=1 and (not interactive) and (user=’Erwin.Kalvelagen’) then
    call delete_constraint_to_confuse_user

Solver works correctly with a =1 equation when used from the GUI.
Well, found some more reports on this strange bug:

• http://www.pcreview.co.uk/forums/problem-solveradd-can-anyone-help-t961905.html
• http://excelforum.com/excel-programming-vba-macros/492647-solved-missing-condition-after-solver-called-by-macro.html
• http://stackoverflow.com/questions/15620177/excel-solver-ignoring-constraint-in-vba

This bug is present in Excel 2010 and 2013 (32 and 64 bit).

Playing with job shop problem ft10 (5)

In http://yetanothermathprogrammingconsultant.blogspot.com/2014/04/playing-with-ft10-job-shop-1.html we saw Gurobi was very successful in solving ft10.gms to optimality. How would the open source solver CBC do? Actually it could not close the gap before hitting an imposed time limit of 1 hour.

The picture does not give us much hope that by extending the time limit we will gain much.

This performance is substantially worse than what we saw with Gurobi.

Playing with job shop problem ft10 (4)

We could not solve my job shop formulations in http://yetanothermathprogrammingconsultant.blogspot.com/2014/04/playing-with-job-shop-problem-ft10-2.html but actually Or-tools has a pretty good C++ based implementation: https://code.google.com/p/or-tools/source/browse/trunk/examples/cpp/jobshop.cc. This can solve the ft10 problem in reasonable time:

c:\Users\erwin\tmp>jobshop --data_file=ft10 [19:25:55] examples\cpp/jobshop.h:131: Reading jssp instance ft10 [19:25:55] examples\cpp/jobshop.h:148: 10 machines and 10 jobs [19:25:55] src/constraint_solver/search.cc:243: Start search (memory used = 4.66 MB) [19:25:55] src/constraint_solver/search.cc:243: Root node processed (time = 1 ms, constraints = 351, memory used = 4.98 MB) [19:25:55] src/constraint_solver/search.cc:243: Solution #0 (objective value = 1740, time = 67 ms, branches = 91, failures = 0, depth = 91, memory used = 5.04 MB) [19:25:55] src/constraint_solver/search.cc:243: Solution #1 (objective value = 1734, objective maximum = 1740, time = 96 ms, branches = 96, failures = 7, depth = 89, memory used = 5.11 MB) [19:25:55] src/constraint_solver/search.cc:243: Solution #2 (objective value = 1729, objective maximum = 1740, time = 128 ms, branches = 101, failures = 13, depth = 87, memory used = 5.11 MB) [19:25:55] src/constraint_solver/search.cc:243: Solution #3 (objective value = 1723, objective maximum = 1740, time = 148 ms, branches = 106, failures = 17, depth = 88, memory used = 5.11 MB) [19:25:55] src/constraint_solver/search.cc:243: Solution #4 (objective value = 1717, objective maximum = 1740, time = 205 ms, branches = 125, failures = 46, depth = 76, memory used = 5.13 MB) [19:25:55] src/constraint_solver/search.cc:243: Solution #5 (objective value = 1685, objective maximum = 1740, time = 233 ms, branches = 136, failures = 55, depth = 78, memory used = 5.13 MB) [19:25:55] src/constraint_solver/search.cc:243: Solution #6 (objective value = 1664, objective maximum = 1740, time = 280 ms, branches = 154, failures = 75, depth = 74, memory used = 5.13 MB) .. [19:28:41] src/constraint_solver/search.cc:243: Solution #151 (objective value = 938, objective maximum = 1740, time = 165613 ms, branches = 534773, failures = 268520, depth = 36, memory used = 5.16 MB) [19:29:36] src/constraint_solver/search.cc:243: Solution #152 (objective value = 935, objective maximum = 1740, time = 221354 ms, branches = 709290, failures = 355782, depth = 40, memory used = 5.16 MB) [19:29:38] src/constraint_solver/search.cc:243: Solution #153 (objective value = 934, objective maximum = 1740, time = 222810 ms, branches = 709292, failures = 355784, depth = 40, memory used = 5.16 MB) [19:29:38] src/constraint_solver/search.cc:243: Solution #154 (objective value = 930, objective maximum = 1740, time = 222951 ms, branches = 709544, failures = 355918, depth = 34, memory used = 5.16 MB) [19:30:13] src/constraint_solver/search.cc:243: Finished search tree (time = 258350 ms, branches = 809795, failures = 406060, memory used = 5.16 MB) [19:30:13] src/constraint_solver/search.cc:243: End search (time = 258361 ms, branches = 809795, failures = 406060, memory used = 5.17 MB, speed = 3134 branches/s) [19:30:13] examples\cpp/jobshop.cc:165: Machine_0: 0, 1, 8, 6, 3, 4, 7, 9, 5, 2 [19:30:13] examples\cpp/jobshop.cc:165: Machine_1: 3, 5, 6, 9, 8, 4, 2, 7, 0, 1 [19:30:13] examples\cpp/jobshop.cc:165: Machine_2: 5, 3, 4, 7, 1, 6, 9, 8, 0, 2 [19:30:13] examples\cpp/jobshop.cc:165: Machine_3: 5, 6, 8, 4, 2, 0, 1, 9, 3, 7 [19:30:13] examples\cpp/jobshop.cc:165: Machine_4: 3, 1, 4, 5, 7, 0, 8, 9, 6, 2 [19:30:13] examples\cpp/jobshop.cc:165: Machine_5: 5, 4, 8, 6, 7, 9, 0, 2, 1, 3 [19:30:13] examples\cpp/jobshop.cc:165: Machine_6: 6, 3, 9, 5, 8, 7, 0, 1, 2, 4 [19:30:13] examples\cpp/jobshop.cc:165: Machine_7: 3, 5, 4, 8, 6, 2, 0, 7, 1, 9 [19:30:13] examples\cpp/jobshop.cc:165: Machine_8: 5, 3, 9, 4, 6, 2, 7, 8, 0, 1 [19:30:13] examples\cpp/jobshop.cc:165: Machine_9: 5, 1, 6, 8, 9, 4, 7, 3, 2, 0 c:\Users\erwin\tmp>

The problem is solved to a proven optimal solution in less than 5 minutes.

Some obvious questions arise:

1. So how is this implementation different from the Minizinc models I did before? One difference is that it is using interval variables. These variables have a start and a duration, and are often used in scheduling models. I am not sure how to use these variable in a Minizinc model.
2. Can we create a Minizinc model with similar performance?
3. The optimization is probably done by:
   1. Find solution
   2. If infeasible stop
   3. Else add the constraint obj < obj_found to the model and go to step 1
   This leads to many solutions being found: 154 to be precise. Would it not be better to use some binary search? This may be a stupid suggestion; but I would guess this could reduce the number of sub-problems to be solved. One could use an LP relaxation to find an initial lower bound. I assume my suggestion is not that good (otherwise it would have been implemented already), but I don’t see immediately why. May be tightening the problem is relatively easy compared to relaxing it.
4. When invoked without a data file name, the program crashes:
   
   Looks like this is caused by an abort() statement (replace by exit(-1) to stop more gracefully).
5. The performance over time looks vey much like a MIP solver:
   
   i.e. quick progress at the beginning and slowing down later on.

Playing with job shop problem ft10 (3)

To see how the two different formulations mentioned in http://yetanothermathprogrammingconsultant.blogspot.com/2014/04/playing-with-job-shop-problem-ft10-2.html compare we use a real small example: ft06. Here are the models:

Original formulation with OR constraints: ft06.mzn

int: numjobs = 6; int: numstages = 6; set of int: Jobs = 1..numjobs; set of int: Stages = 1..numstages; array[Jobs,Stages] of int: ProcTimes = [| 1,     3,     6,     7,     3,     6,   | 8,     5,    10,    10,    10,     4,   | 5,     4,     8,     9,     1,     7,   | 5,     5,     5,     3,     8,     9,   | 9,     3,     5,     4,     3,     1,   | 3,     3,     9,    10,     4,     1 |]; array[Jobs,Stages] of int: Machine = [| 2,   0,   1,   3,   5,   4,   | 1,   2,   4,   5,   0,   3,   | 2,   3,   5,   0,   1,   4,   | 1,   0,   2,   3,   4,   5,   | 2,   1,   4,   5,   0,   3,   | 1,   3,   5,   0,   4,   2 |]; int: horizon = sum([ ProcTimes[j,s] | j in Jobs, s in Stages]); array[Jobs,Stages] of var 0..horizon: Start; var 0..horizon: makespan; % order constraint    forall (j in Jobs, t in 1..numstages-1) (       Start[j,t+1] >= Start[j,t] + ProcTimes[j,t]    ); % no overlap constraint    forall (i in Jobs, j in Jobs where i<j) (      forall (ti in Stages, tj in Stages              where Machine[i,ti]=Machine[j,tj]) (         Start[i,ti] >= Start[j,tj] + ProcTimes[j,tj] \/         Start[j,tj] >= Start[i,ti] + ProcTimes[i,ti] )      ); constraint    makespan =     max( [ Start[j,numstages] + ProcTimes[j,numstages] | j in Jobs] ); solve minimize makespan; output ["makespan:",show(makespan),"\n",show(Start)]

Formulation with cumulative constraint: ft06c.mzn

include "globals.mzn"; int: numjobs = 6; int: numstages = 6; int: nummachines = 6; set of int: Jobs = 1..numjobs; set of int: Stages = 1..numstages; set of int: Machines = 0..nummachines-1; array[Jobs,Stages] of int: ProcTimes = [| 1,     3,     6,     7,     3,     6,   | 8,     5,    10,    10,    10,     4,   | 5,     4,     8,     9,     1,     7,   | 5,     5,     5,     3,     8,     9,   | 9,     3,     5,     4,     3,     1,   | 3,     3,     9,    10,     4,     1 |]; array[Jobs,Stages] of Machines: Machine = [| 2,   0,   1,   3,   5,   4,   | 1,   2,   4,   5,   0,   3,   | 2,   3,   5,   0,   1,   4,   | 1,   0,   2,   3,   4,   5,   | 2,   1,   4,   5,   0,   3,   | 1,   3,   5,   0,   4,   2 |]; int: horizon = sum([ ProcTimes[j,s] | j in Jobs, s in Stages]); array[Jobs,Stages] of var 0..horizon: Start; var 0..horizon: makespan; % order constraint    forall (j in Jobs, t in 1..numstages-1) (       Start[j,t+1] >= Start[j,t] + ProcTimes[j,t]    ); % no overlap constraint    forall (m in Machines) (        cumulative([ Start[j,t]     | j in Jobs, t in Stages where Machine[j,t]=m ],                   [ ProcTimes[j,t] | j in Jobs, t in Stages where Machine[j,t]=m ],                   [ 1              | j in Jobs, t in Stages where Machine[j,t]=m ],                   1)    ); constraint    makespan =     max( [ Start[j,numstages] + ProcTimes[j,numstages] | j in Jobs] ); solve minimize makespan; output ["makespan:",show(makespan),"\n",show(Start)]

Comparison

Solution time in seconds

Solver	or ft06.mzn	cumulative ft06c.mnz	Command line
g12fd	0.3	0.2	mzn-g12fd –s ft06.mzn
g12lazy	0.2	6.5	mzn-g12lazy -s ft06.mzn
gecode	0.1	0.1	mzn-gecode -s ft06.mzn
or-tools	147	0.1	minizinc -G or-tools -f \tmp\fz.exe ft06.mzn

Gecode and or-tools show some statistics for these case:

Playing with job shop problem ft10 (2)

How would a Constraint Programming formulation do on this problem: http://yetanothermathprogrammingconsultant.blogspot.com/2014/04/playing-with-ft10-job-shop-1.html. A straightforward translation of the MIP formulation into Minizinc can look like:

int: numjobs = 10; int: numstages = 10; set of int: Jobs = 1..numjobs; set of int: Stages = 1..numstages; array[Jobs,Stages] of int: ProcTimes = [| 29, 78,  9, 36, 49, 11, 62, 56, 44, 21,   | 43, 90, 75, 11, 69, 28, 46, 46, 72, 30,   | 91, 85, 39, 74, 90, 10, 12, 89, 45, 33,   | 81, 95, 71, 99,  9, 52, 85, 98, 22, 43,   | 14,  6, 22, 61, 26, 69, 21, 49, 72, 53,   | 84,  2, 52, 95, 48, 72, 47, 65,  6, 25,   | 46, 37, 61, 13, 32, 21, 32, 89, 30, 55,   | 31, 86, 46, 74, 32, 88, 19, 48, 36, 79,   | 76, 69, 76, 51, 85, 11, 40, 89, 26, 74,   | 85, 13, 61,  7, 64, 76, 47, 52, 90, 45 |]; array[Jobs,Stages] of int: MachineNumbers = [|  0, 1, 2, 3, 4, 5, 6, 7, 8, 9,   |  0, 2, 4, 9, 3, 1, 6, 5, 7, 8,   |  1, 0, 3, 2, 8, 5, 7, 6, 9, 4,   |  1, 2, 0, 4, 6, 8, 7, 3, 9, 5,   |  2, 0, 1, 5, 3, 4, 8, 7, 9, 6,   |  2, 1, 5, 3, 8, 9, 0, 6, 4, 7,   |  1, 0, 3, 2, 6, 5, 9, 8, 7, 4,   |  2, 0, 1, 5, 4, 6, 8, 9, 7, 3,   |  0, 1, 3, 5, 2, 9, 6, 7, 4, 8,   |  1, 0, 2, 6, 8, 9, 5, 3, 4, 7 |]; int: horizon = sum([ ProcTimes[j,s] | j in Jobs, s in Stages]); array[Jobs,Stages] of var 0..horizon: Start; var 0..horizon: makespan; % positive variables constraint    forall (j in Jobs) (       Start[j,1]>=0    ); % order constraint    forall (j in Jobs, t in 1..numstages-1) (       Start[j,t+1] >= Start[j,t] + ProcTimes[j,t]    ); % no overlap constraint    forall (i in Jobs, j in Jobs where i<j) (      forall (ti in Stages, tj in Stages              where MachineNumbers[i,ti]=MachineNumbers[j,tj]) (         Start[i,ti] >= Start[j,tj] + ProcTimes[j,tj] \/         Start[j,tj] >= Start[i,ti] + ProcTimes[i,ti] )      ); constraint    makespan =     max( [ Start[j,numstages] + ProcTimes[j,numstages] | j in Jobs] ); solve minimize makespan;

This looks actually quite nice. We can drop the binary variables that deal with the overlap, and the objective is more intuitive. As most CP solvers don’t deal very well or not at all with continuous variables, we used integer variables. This is ok here as we deal with integer valued processing times. In the real world you may need to rescale and/or approximate these numbers. Unfortunately this model does not solve. I am looking at the cursor and don’t see any feedback about any progress:

There is an alternative formulation that is often much better: replace the no overlap constraints by a global constraint called cumulative. Not totally intuitive but we can translate the model quite easily. In addition we added some bounds on all variables:

include "globals.mzn"; int: numjobs = 10; int: numstages = 10; int: nummachines = 10; set of int: Jobs = 1..numjobs; set of int: Stages = 1..numstages; set of int: Machines = 0..nummachines-1; array[Jobs,Stages] of int: ProcTimes = [| 29, 78,  9, 36, 49, 11, 62, 56, 44, 21,   | 43, 90, 75, 11, 69, 28, 46, 46, 72, 30,   | 91, 85, 39, 74, 90, 10, 12, 89, 45, 33,   | 81, 95, 71, 99,  9, 52, 85, 98, 22, 43,   | 14,  6, 22, 61, 26, 69, 21, 49, 72, 53,   | 84,  2, 52, 95, 48, 72, 47, 65,  6, 25,   | 46, 37, 61, 13, 32, 21, 32, 89, 30, 55,   | 31, 86, 46, 74, 32, 88, 19, 48, 36, 79,   | 76, 69, 76, 51, 85, 11, 40, 89, 26, 74,   | 85, 13, 61,  7, 64, 76, 47, 52, 90, 45 |]; array[Jobs,Stages] of int: Machine = [|  0, 1, 2, 3, 4, 5, 6, 7, 8, 9,   |  0, 2, 4, 9, 3, 1, 6, 5, 7, 8,   |  1, 0, 3, 2, 8, 5, 7, 6, 9, 4,   |  1, 2, 0, 4, 6, 8, 7, 3, 9, 5,   |  2, 0, 1, 5, 3, 4, 8, 7, 9, 6,   |  2, 1, 5, 3, 8, 9, 0, 6, 4, 7,   |  1, 0, 3, 2, 6, 5, 9, 8, 7, 4,   |  2, 0, 1, 5, 4, 6, 8, 9, 7, 3,   |  0, 1, 3, 5, 2, 9, 6, 7, 4, 8,   |  1, 0, 2, 6, 8, 9, 5, 3, 4, 7 |]; int: last_end = sum([ ProcTimes[j,s] | j in Jobs, s in Stages]); int: last_start = last_end - min([ ProcTimes[j,numstages] | j in Jobs ]); array[Jobs,Stages] of var 0..last_start: Start; var 0..last_end: makespan; % order constraint    forall (j in Jobs, t in 1..numstages-1) (       Start[j,t+1] >= Start[j,t] + ProcTimes[j,t]    ); % no overlap constraint    forall (m in Machines) (        cumulative([ Start[j,t]     | j in Jobs, t in Stages where Machine[j,t]=m ],                   [ ProcTimes[j,t] | j in Jobs, t in Stages where Machine[j,t]=m ],                   [ 1              | j in Jobs, t in Stages where Machine[j,t]=m ],                   1)    ); constraint    makespan =     max( [ Start[j,numstages] + ProcTimes[j,numstages] | j in Jobs] ); % helper constraint    forall (j in Jobs, t in 1..numstages-1) (       Start[j,t+1] >= sum([ProcTimes[j, tt] | tt in 1..t])    ); solve minimize makespan;

Unfortunately still just a blinking cursor…

Any better Minizinc formulation available? Here are some alternative formulations which I have not tried out:

• https://github.com/MiniZinc/minizinc-benchmarks/blob/master/jobshop/jobshop.mzn
• https://github.com/hakank/hakank/blob/master/minizinc/jobshop.mzn

Some questions:

1. No log when solving the models? One would like to see some progress log.
2. How to debug models? Something like a limrow/limcol in GAMS or expand in AMPL? One could look at the “flatzinc” output, but that is difficult to digest.
3. Can we set a time limit and then get the best solution so far?

Playing with job shop problem ft10 (1)

As discussed in http://yetanothermathprogrammingconsultant.blogspot.com/2009/09/job-shop-scheduling.html a MIP solver like Gurobi can solve this difficult problem quite easily.

Here we show the performance with 1 and 4 threads:

The big advantage of using a MIP solver is that any time (after finding the first integer solution) we have both a best found (upper bound) and best possible or best bound (lower bound) available. This not only gives us a proven optimal solution at the end but a sense of the quality of the solution during the solution process. We can interrupt before the end using this information (e.g. by stopping on a small gap).

There are a few interesting observations:

• The 4 thread integer solutions are not uniformly better than their 1 thread counterparts: quite often the red line (top part of the graph) is below the blue line
• But in the end 4 threads wins big
• Most progress is achieved in the beginning w.r.t. to finding good integer solutions. So when in a hurry we can stop early.
• This also means that building a heuristic that finds a good solution quickly is of limited value: the MIP solver finds good solutions quickly on its own. I.e. such a heuristic helps where the MIP solver does not need much help.
• The plot was produced with R and ggplot. I think it looks quite nice.

GAMS model

$ontext     Job Shop Scheduling     Manne formulation     Alan Manne, "On the job-shop scheduling problem", Operations Research     vol 8, no 2 March-April 1960.     Data set ft10 is from:     H. Fisher, G. L. Thompson, Probabilistic learning combinations of     local job-shop scheduling rules, in: J. F. Muth, G. L. Thompson (eds.),     Industrial Scheduling, Prentice Hall, Englewood Cliffs, N.J., 1963.  job1:   0 29 ; 1 78 ; 2  9 ; 3 36 ; 4 49 ; 5 11 ; 6 62 ; 7 56 ; 8 44 ; 9 21  job2:   0 43 ; 2 90 ; 4 75 ; 9 11 ; 3 69 ; 1 28 ; 6 46 ; 5 46 ; 7 72 ; 8 30  job3:   1 91 ; 0 85 ; 3 39 ; 2 74 ; 8 90 ; 5 10 ; 7 12 ; 6 89 ; 9 45 ; 4 33  job4:   1 81 ; 2 95 ; 0 71 ; 4 99 ; 6  9 ; 8 52 ; 7 85 ; 3 98 ; 9 22 ; 5 43  job5:   2 14 ; 0  6 ; 1 22 ; 5 61 ; 3 26 ; 4 69 ; 8 21 ; 7 49 ; 9 72 ; 6 53  job6:   2 84 ; 1  2 ; 5 52 ; 3 95 ; 8 48 ; 9 72 ; 0 47 ; 6 65 ; 4  6 ; 7 25  job7:   1 46 ; 0 37 ; 3 61 ; 2 13 ; 6 32 ; 5 21 ; 9 32 ; 8 89 ; 7 30 ; 4 55  job8:   2 31 ; 0 86 ; 1 46 ; 5 74 ; 4 32 ; 6 88 ; 8 19 ; 9 48 ; 7 36 ; 3 79  job9:   0 76 ; 1 69 ; 3 76 ; 5 51 ; 2 85 ; 9 11 ; 6 40 ; 7 89 ; 4 26 ; 8 74  job10:  1 85 ; 0 13 ; 2 61 ; 6  7 ; 8 64 ; 9 76 ; 5 47 ; 3 52 ; 4 90 ; 7 45   Description: jobs need to follow a sequence of operations. The numbers indicate   machine number and processing time.   This is a well-known benchmark problem and the optimal obj=930. $offtext set   j 'tasks' / job1*job10/   t 'stages'  /t1*t10/ ; table proctime(j,t) 'processing times for each stage'         t1    t2    t3    t4    t5    t6    t7    t8    t9   t10 job1    29    78     9    36    49    11    62    56    44   21 job2    43    90    75    11    69    28    46    46    72   30 job3    91    85    39    74    90    10    12    89    45   33 job4    81    95    71    99     9    52    85    98    22   43 job5    14     6    22    61    26    69    21    49    72   53 job6    84     2    52    95    48    72    47    65     6   25 job7    46    37    61    13    32    21    32    89    30   55 job8    31    86    46    74    32    88    19    48    36   79 job9    76    69    76    51    85    11    40    89    26   74 job10   85    13    61     7    64    76    47    52    90   45 ; table machine(j,t) 'machine numbers for each stage (zero based)'         t1  t2  t3  t4  t5  t6  t7  t8  t9  t10 job1    0    1   2   3   4   5   6   7   8   9 job2    0    2   4   9   3   1   6   5   7   8 job3    1    0   3   2   8   5   7   6   9   4 job4    1    2   0   4   6   8   7   3   9   5 job5    2    0   1   5   3   4   8   7   9   6 job6    2    1   5   3   8   9   0   6   4   7 job7    1    0   3   2   6   5   9   8   7   4 job8    2    0   1   5   4   6   8   9   7   3 job9    0    1   3   5   2   9   6   7   4   8 job10   1    0   2   6   8   9   5   3   4   7 ; alias (j,j2),(t,t2); set ovl(j,t,j2,t2) 'this subset of (j,t),(j2,t2) needs to be checked against overlap'; ovl(j,t,j2,t2)$(ord(j)<ord(j2) and machine(j,t)=machine(j2,t2)) = yes; variables   x(j,t)        'start time of subtask'   y(j,t,j2,t2)  'binary variable to implement non-overlap: (j,t) before or after (j2,t2)'   z             'objective variable' ; binary variable y; positive variable x; scalar TMAX 'max time horizon'; TMAX = sum((j,t), proctime(j,t)); equations    NoOverlap1(j,t,j2,t2)  'machine overlap'    NoOverlap2(j,t,j2,t2)  'machine overlap'    Precedence(j,t)        'orders need to follow a certain sequence of machines'    zmax(j,t)              'make span' ; * * each task within a job should start after previous one has finished * Precedence(j,t)$(ord(t)<card(t)).. x(j,t+1) =G= x(j,t) + proctime(j,t); * * tasks on a machine cannot overlap: * execute either before or after * NoOverlap1(ovl(j,t,j2,t2)).. x(j2,t2) =G= x(j,t) + proctime(j,t) - TMAX*y(j,t,j2,t2); NoOverlap2(ovl(j,t,j2,t2)).. x(j,t) =G= x(j2,t2) + proctime(j2,t2) - TMAX*(1-y(j,t,j2,t2)); * * minimize completion time of last task * zmax(j,t).. z =G= x(j,t) + proctime(j,t); option optcr=0; model jobshop /all/; solve jobshop minimizing z using mip;

R Code to create the plot

library(ggplot2)   setwd("C:/projects/tmp") # read csv files d1<-read.csv("1thread.csv") d4<-read.csv("4thread.csv") # stack them into a single data frame d<-rbind(d1,d4) # add a Threads column indicating the data set d$Threads <- c(rep("1 thread",nrow(d1)),rep("4 threads",nrow(d4))) # convert factor to double ("na" will be converted to NA) d$bestFound <- as.double(as.character(d$bestFound)) # actual plotting ggplot(data=d)+ geom_line(aes(group=Threads,x=seconds,y=bestBound,color=Threads))+ geom_line(aes(group=Threads,x=seconds,y=bestFound,color=Threads))+ ggtitle("Gurobi laptop performance on ft10.gms")+ xlab("Time (seconds)")+ ylab("Best Found (top), Best Bound (bottom)") Created by Pretty R at inside-R.org

Cleaning up the GAMS log

When running a large model the standard GAMS log may dump a large amount of more or less uninformative text to the screen:

After cleaning this up it looks a little bit more frugal, but actually gives a better idea of where you are in the solution progress: