> My large QP portfolio model does not solve with GAMS/KNITRO.
Yes, for large problems you will get:
Memory estimate for Hessian is too small.
Increase the <modelname>.workfactor option from the current value of 1
For 2000 stocks with WORKFACTOR=10 I got the same error.
Even if the model is formulated as a QCP model, the GAMS link is not smart enough in setting up the hessian efficiently. Instead it looks like the QP is handled as a general NLP.
There are two easy workarounds. First of all you can solve this with IPOPT. The GAMS link for IPOPT is smarter in dealing with second derivatives than the link for KNITRO (as of GAMS 23.5). Note that it is better to solve as a QCP model than as an NLP model: GAMS is not smart enough to recognize this as a QP and exploit that:
model type GAMS generation time IPOPT time function evaluation time Total solver time NLP 38 21.8 39.1 61.0 QCP 38 21.6 9.8 31.4
A second possibility is to reformulate model (1):
into model (2):
This formulation can be solved with KNITRO without the problems with the hessian storage.
As an aside we can improve formulation 1 by replacing the variance-covariance matrix Q by
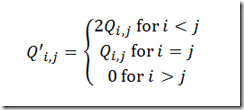
model type GAMS generation time IPOPT time function evaluation time Total solver time QCP –triangular Q 18.8 21.3 4.6 26
We can also apply the triangular storage scheme to model (2). With a solver like SNOPT this leads to a very fast total solution time (i.e. generation time + solver time).
model type GAMS generation time SNOPT time NLP –triangular Q in linear constraints 1 5
If needed we can even speed this up by not using the covariances but rather the mean adjusted returns directly:
I used T=300 time periods. This formulation yields:
model type GAMS generation time SNOPT time NLP – Mean Adj Returns 0.5 2.3
Even for the simple QP portfolio model, careful modeling can help to improve the performance in a significant way.


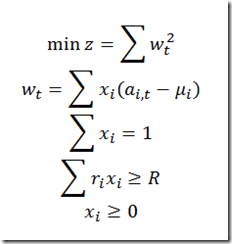
In many cases you can do these models quite efficiently using conic optimization which is supported in GAMS. Note all issues with Hessian complete vanishes because there no Hessian in conic optimization.
ReplyDeleteThe note
http://www.mosek.com/fileadmin/reports/tech/portfolio.pdf
tells how to reformulate your problem as conic problem.
On a small GAMS example Michael B. and tried with MOSEK the conic formulation led faster solution times.
Mosek can solve this very fast as conic problem, but its solution is a little bit sloppy. With this data set it will be rejected as infeasible when fed into Mosek as QP. I have noticed that behavior also with other (large) data sets. Somehow all the formulations I showed, demonstrated better numerical behavior.
ReplyDeleteI am a bit confused. MOSEK can also solve it as QP and that is something different from a conic formulation. So if you input it as QP then you are not using the conic optimizer.
ReplyDeleteThe QP optimizer may sometimes say infeasible when it should not but that usually indicate a bad problem scaling (large numbers somewhere). Also there is there is parameter that can be set so it is more conservative about scaling infeasible. If I can see the log file I might be able to come up with a solution.
Finally, regarding formulation then quite frequently you can reformulate the problem to have diagonal Q at the cost of increasing the number linear constraints and variables (as discussed in our note). This is in many cases advantageous for the interior-point optimizers.
But I am sure you aware of that trick.
The sanity check for the conic solution was:
ReplyDelete1. Solve conic model
2. Fix: x.fx(i) = x.l(i);
3. Solve QP => INFEASIBLE.
I.e. the conic solver does not deliver a solution that is within feasibility tolerances.
Maybe there is bug somewhere. Without running the problem it is hard to say though. If you submit the problem to GAMS support or MOSEK support (support@mosek.com) we shall look at it.
ReplyDeleteThe model data is too big to email.
ReplyDeleteProblem source is here: http://amsterdamoptimization.com/models/cone/portfcone.gms. Data is here: http://amsterdamoptimization.com/models/cone/portf.gdx. Here I just do:
1. Solve conic problem
2. Fix:x.fx(i) = x.l(i);
3. Solve conic problem
The second model will be declared infeasible. (The budget equation is actually violated by more than 1e-6).