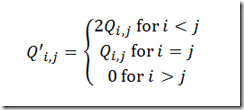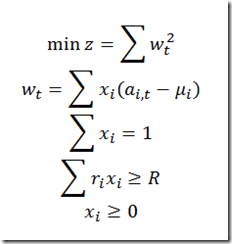Long running horizon

I am experimenting with a timber model. These models have typically long horizons, which can cause some problems with some solvers. As the model has a nonlinear objective I tried a few NLP solvers:

Solver	Objective (maximize)
Conopt	104599.7740
Minos	53746.0234
Snopt	6651.1413

This looks pretty bad. Fortunately, a simple option setting: SCALE OPTION = 0, can make things much better:

Solver	Objective (maximize)
Minos (no scaling)	104599.7740
Snopt (no scaling)	104599.6879

Intuitively this makes some sense: MINOS and SNOPT scale by default only the linear variables. This strategy is actually not without merit: the Jacobian elements for these nonlinear variables can change quite a lot during the optimization, so scaling based on the initial Jacobian elements may not be very wise. However, in some cases making this distinction between linear and nonlinear variables can make things worse. In this case it is better not to scale at all.

I was first tinkering with the optimality tolerance, as I have seen with other forestry models (LP and NLP) that for these ridiculously long time horizons, tightening the optimality tolerance can help getting better solutions. For this model that was not the case.

Cplex new version

In some cases a new version of a solver can perform worse on some models. Here is a particular unfortunate example, where Cplex 12.1 finds several very good solutions in the initial heuristics, but Cplex 12.2 just fails to find any integer solutions within the allotted time: 

ILOG CPLEX       Nov  1, 2009 23.3.3 WEX 13908.15043 WEI x86_64/MS Windows Cplex 12.1.0, GAMS Link 34 Cplex licensed for 1 use of parallel lp, qp, mip and barrier. Cplex MIP uses 1 of 4 parallel threads. Change default with option THREADS. Reading data... Starting Cplex.… … Root relaxation solution time =  102.77 sec.         Nodes                                         Cuts/    Node  Left     Objective  IInf  Best Integer     Best Node    ItCnt     Gap       0     0    15053.5468   150                  15053.5468   151633         *     0+    0                       150008.6529    15053.5468   151633   89.96%       0     0    15065.0166   146   150008.6529     Cuts: 479   158521   89.96% *     0+    0                        15387.9888    15065.0166   158521    2.10%       0     0    15065.1974   152    15387.9888 Flowcuts: 146   159618    2.10%       0     0    15065.2096   146    15387.9888      Cuts: 70   159894    2.10%       0     0    15065.2104   146    15387.9888   Flowcuts: 9   159952    2.10% *     0+    0                        15175.4264    15065.2104   159952    0.73% Flow cuts applied:  472 Mixed integer rounding cuts applied:  4 Gomory fractional cuts applied:  7 MIP status(102): integer optimal, tolerance

 

IBM ILOG CPLEX   Jul  4, 2010 23.5.1 WEX 18414.18495 WEI x86_64/MS Windows Cplex 12.2.0.0, GAMS Link 34 GAMS/Cplex licensed for continuous and discrete problems. Cplex MIP uses 1 of 4 parallel threads. Change default with option THREADS. Reading data... Starting Cplex... … Root relaxation solution time =  107.14 sec.         Nodes                                         Cuts/    Node  Left     Objective  IInf  Best Integer     Best Node    ItCnt     Gap       0     0    15053.5468   111                  15053.5468   120941               0     0    15066.3609   105                   Cuts: 787   126925               0     0    15067.4221    99                     Cuts: 7   127524               0     0    15067.4512   100                     Cuts: 8   127557               0     0    15067.4512   100                  MIRcuts: 2   127559         Heuristic still looking. Heuristic still looking.       0     2    15067.4512   100                  15067.4561   127559         Elapsed real time = 237.15 sec. (tree size =  0.00 MB, solutions = 0)       1     3    15072.3309    97                  15067.4561   131486               2     4    15068.7687    75                  15068.8163   134032               3     5    15069.6752    84                  15068.8163   134657               4     6    15071.3502    88                  15069.6828   135922               5     7    15072.3709    75                  15069.6828   136786               6     8    15086.2295    77                  15069.6828   145563               7     9    15072.9117    71                  15069.6828   146885               8    10    15073.9185    79                  15069.6828   148355               9    11    15081.7555    70                  15069.6828   154282              12    14    15074.6296    72                  15069.6828   154696         Elapsed real time = 314.54 sec. (tree size =  2.27 MB, solutions = 0)      13    15    15088.4559    66                  15069.6828   159070         … MIP status(108): time limit exceeded, no integer solution CPLEX Error  1217: No solution exists. Resource limit exceeded, no integer solution found.

Such behavior is always difficult to explain to a customer. The argument that on average a new version tends to do better is of little consolation.

PS. The time limit was very tight on this model: 400 seconds (extremely tight considering the LP takes 100 seconds). This was no problem with previous versions of Cplex as the initial heuristic always found solutions very quickly. These solutions were so good they already obeyed the requested gap of 0.8%. Cplex 12.2 finds the solution relatively quickly in the B&B after about 500 seconds on my machine with 1 thread (the client on his machine obtained no solution in 600 seconds with 2 threads and some other solver options; I assume a little bit more time may help here).

PS2. All my runs were with default settings (except 1 thread, gap=0.8%, time limit=400 seconds).

QP Models with GAMS/Knitro

> My large QP portfolio model does not solve with GAMS/KNITRO.

Yes, for large problems you will get:

Memory estimate for Hessian is too small.
Increase the <modelname>.workfactor option from the current value of 1

For 2000 stocks with WORKFACTOR=10 I got the same error.

Even if the model is formulated as a QCP model, the GAMS link is not smart enough in setting up the hessian efficiently. Instead it looks like the QP is handled as a general NLP.

There are two easy workarounds. First of all you can solve this with IPOPT. The GAMS link for IPOPT is smarter in dealing with second derivatives than the link for KNITRO (as of GAMS 23.5). Note that it is better to solve as a QCP model than as an NLP model: GAMS is not smart enough to recognize this as a QP and exploit that:

model type	GAMS generation time	IPOPT time	function evaluation time	Total solver time
NLP	38	21.8	39.1	61.0
QCP	38	21.6	9.8	31.4

A second possibility is to reformulate model (1):

into model (2):

This formulation can be solved with KNITRO without the problems with the hessian storage.

---

As an aside we can improve formulation 1 by replacing the variance-covariance matrix Q by

We exploit here symmetry in the quadratic form x’Qx. This exercise substantially reduces the GAMS generation time, and also further shaves off some time from the solver:

model type	GAMS generation time	IPOPT time	function evaluation time	Total solver time
QCP –triangular Q	18.8	21.3	4.6	26

We can also apply the triangular storage scheme to model (2). With a solver like SNOPT this leads to a very fast total solution time (i.e. generation time + solver time).

model type	GAMS generation time	SNOPT time
NLP –triangular Q in linear constraints	1	5

If needed we can even speed this up by not using the covariances but rather the mean adjusted returns directly:

I used T=300 time periods. This formulation yields:

model type	GAMS generation time	SNOPT time
NLP – Mean Adj Returns	0.5	2.3

Even for the simple QP portfolio model, careful modeling can help to improve the performance in a significant way.

Simplex vs barrier

For some models the barrier algorithm is very fast compared to the Simplex method (for an example see http://yetanothermathprogrammingconsultant.blogspot.com/2009/01/cplex-barrier-results.html). Here is an example of a medium sized but quite dense problem (107543 rows, 81160 columns, 878481 nonzeroes), for which the opposite holds. The primal and dual simplex method of the leading solvers are all doing very good, and the interior point algorithms have some troubles. In addition the variability between interior point timings is much more pronounced than the variability between Simplex times.

Timings are in seconds. The fastest barrier is 306 secs.

Gurobi recovery in difficult LP

It is interesting to see how Gurobi recovers from numerical trouble in a difficult (dense) LP, when using the primal simplex algorithm:

Iteration    Objective       Primal Inf.    Dual Inf.      Time
       0    1.6911927e+08   0.000000e+00   1.779242e+04      1s
    9864    1.4022077e+06   0.000000e+00   6.819017e+01      5s
Warning: 1 variables dropped from basis
Warning: switch to quad precision
   13988    1.3343358e+06   0.000000e+00   1.064917e+02     10s
   14726    1.3299619e+06   0.000000e+00   0.000000e+00     13s

Apparently it switches to quadruple precision. Those are REAL*16 numbers, yielding approx. 34 decimal digits of precision. I don’t think I have ever seen this capability in other solvers.

OR in MIP

Question: If we have two non-negative variables, X1, X2 >= 0 and we know at least one of them is zero. How shall we linearize the constraints? In other word, the constraints are:
X1>= 0
X2 >=0
X1*X2 = 0.

The details are very much problem dependent, but

x1*x2 =0

can be formulated as

x1 <= 0 OR  X2 <= 0

i.e.

x1 <= M1*b
x2 <= M2*(1-b)
b in {0,1}
M1 = (tight) upper bound on X1 (constant)
M2 = (tight) upper bound on X2 (constant)

Solver Foundation CSP: Min/Max

>I want to use Min and Max operators to find the Minimum and maximum value for an array. This array has
>decision variables involved. If Solver Foundation does not support Min and Max operators, do you have any
>other idea to finish such operations?

The current version of Microsoft Solver Foundation is missing Min and Max as in

y == Min[Foreach[{i,I},x[i]]]

One simple alternative is:

    Foreach[{i,I},y<=x[i]],
    Or[Foreach[{i,I},y==x[i]]]

No doubt this will be fixed in the next release.