MIQP bounds and performance

Cplex automatic reformulations

The performance of MIQP models is not always predictable. Here are the results for a small model we used to reproduce a performance issue with Cplex:

Looks like Cplex is attempting a smart reformulation that fails terribly. An indication is the log line:

Reduced MIQP objective Q matrix has 1 nonzeros.

Also the negative best bound (compare this to the relaxed objective) is an indication.

There are two ways to fix the problem. A small reformulation that simplifies the objective, leads to much better performance:

  

In this case the objective is written as a sum of squares of continuous variables, and this prohibits Cplex to do their reformulations. The second way is to use option qtolin and set it to zero.

See: http://www-01.ibm.com/support/knowledgecenter/SSSA5P_12.6.1/ilog.odms.cplex.help/CPLEX/Parameters/topics/QToLin.html?lang=en.

The same issue is discussed in:

• http://bob4er.blogspot.com/2015/03/quadratic-optimization-mysteries-part-1.html
• http://bob4er.blogspot.com/2015/03/quadratic-optimization-mysteries-part-2.html

With a slight variation of this model we can make Mosek look bad. This variant of the model can be easily linearized, which helps tremendously in this case.

The linearized model solves very easily, although there are some bugs with reporting the correct gap. This gap should be 0%, but instead we see:

Best possible: +inf
Absolute gap:       3.000000E+300
Relative gap:            1.000000

This could be related to the relaxed LP having integer values.

Scary numbers

In http://lists.gnu.org/archive/html/help-glpk/2015-04/msg00031.html we see GLPK failing with some scary looking messages:

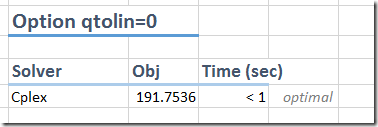
With glpk 4.52 and with the attached input, I get the following failure/error:

------------------------------------------------------------------------------
$ glpsol --lp mi.cplex

Warning: numerical instability (primal simplex, phase I)
   2979: obj =   1.092652474e+04  infeas =  5.265e+09 (0)
Warning: numerical instability (primal simplex, phase I)
   2996: obj =   1.092637382e+04  infeas =  5.260e+09 (0)
   3000: obj =   1.092644011e+04  infeas =  5.235e+09 (0)
Warning: numerical instability (primal simplex, phase I)
   3051: obj =   1.077725595e+04  infeas =  5.201e+09 (0)
Warning: numerical instability (primal simplex, phase I)
   3059: obj =   1.074805814e+04  infeas =  5.185e+09 (0)
Warning: numerical instability (primal simplex, phase I)
   3122: obj =   1.998434476e+03  infeas =  3.955e+05 (0)
Warning: numerical instability (primal simplex, phase I)
   3159: obj =   1.998431624e+03  infeas =  3.944e+05 (0)
Error: unable to factorize the basis matrix (1)
Sorry, basis recovery procedure not implemented yet
glp_intopt: cannot solve LP relaxation
Time used:   1.7 secs
Memory used: 10.8 Mb (11322915 bytes)
--------------------------------------------------------------

Any insights/workarounds will be appreciated.

Even more scary is the following part of the log:

Scaling...
A: min|aij| =  1.000e+00  max|aij| =  2.306e+18  ratio =  2.306e+18
GM: min|aij| =  1.213e-04  max|aij| =  8.246e+03  ratio =  6.800e+07
EQ: min|aij| =  1.480e-08  max|aij| =  1.000e+00  ratio =  6.755e+07
2N: min|aij| =  1.490e-08  max|aij| =  1.500e+00  ratio =  1.007e+08

Commercial solvers typically do much better on these kind of poorly scaled models. As the attached problem file was called mi.cplex, I tried Cplex’s DropSolve on-line tool on this problem. It solves it quickly:

Changed parameter CPX_PARAM_THREADS from 0 to 12
Param[1,067] = 12
Param[1,130] = UTF-8
Param[1,132] = -1
Tried aggregator 1 time.
MIP Presolve eliminated 535 rows and 0 columns.
MIP Presolve modified 38 coefficients.
Reduced MIP has 4312 rows, 345 columns, and 48488 nonzeros.
Reduced MIP has 152 binaries, 193 generals, 0 SOSs, and 0 indicators.
Presolve time = 0.02 sec. (16.48 ticks)
Found incumbent of value 1.2193885e+12 after 0.05 sec. (30.35 ticks)
Probing time = 0.11 sec. (6.03 ticks)
Tried aggregator 1 time.
Reduced MIP has 4312 rows, 345 columns, and 48488 nonzeros.
Reduced MIP has 152 binaries, 193 generals, 0 SOSs, and 0 indicators.
Presolve time = 0.01 sec. (11.80 ticks)
Probing time = 0.11 sec. (5.81 ticks)
Clique table members: 744.
MIP emphasis: balance optimality and feasibility.
MIP search method: dynamic search.
Parallel mode: deterministic, using up to 12 threads.
Root relaxation solution time = 0.08 sec. (17.25 ticks)

        Nodes                                         Cuts/
   Node  Left     Objective  IInf  Best Integer    Best Bound    ItCnt     Gap

*     0+    0                       1.21939e+12     -228.0000           100.00%
*     0+    0                       1.21939e+12     -228.0000           100.00%
*     0+    0                       1.21939e+12     -228.0000           100.00%
      0     0        0.0000    76   1.21939e+12        0.0000      190  100.00%
      0     0       22.2000   114   1.21939e+12     Fract: 76      663  100.00%
*     0+    0                       6.45608e+11       22.2000           100.00%
      0     2       22.2000   114   6.45608e+11       22.2000      663  100.00%
Elapsed time = 1.08 sec. (582.03 ticks, tree = 0.00 MB, solutions = 4)
*     3+    3                       137054.0000       23.0197            99.98%
      3     5      820.0414   170   137054.0000       23.0197     2837   99.98%
     13    15      963.0516   223   137054.0000      822.1327     5049   99.40%
*   156   119      integral     0     4281.0000      822.1327    12517   80.80%
    160    65     4266.0500   109     4281.0000      858.1613    12976   79.95%
*   197    31      integral     0     4278.0000      858.1613    13771   79.94%
*   207    21      integral     0     4275.0000      858.1613    13951   79.93%

Gomory fractional cuts applied:  76

Root node processing (before b&c):
  Real time             =    1.06 sec. (578.93 ticks)
Parallel b&c, 12 threads:
  Real time             =    1.62 sec. (1062.86 ticks)
  Sync time (average)   =    1.06 sec.
  Wait time (average)   =    1.10 sec.
                          ------------
Total (root+branch&cut) =    2.67 sec. (1641.79 ticks)
Incumbent solution:
MILP objective                                 4.2750000000e+03
MILP solution norm |x| (Total, Max)            1.36000e+02  6.00000e+00
MILP solution error (Ax=b) (Total, Max)        2.02749e-12  1.13687e-13
MILP x bound error (Total, Max)                3.15081e-13  1.05027e-13
MILP x integrality error (Total, Max)          1.22169e-12  2.08722e-13
MILP slack bound error (Total, Max)            7.46694e-11  1.98952e-12
integer optimal solution (101)

I would certainly double check the solution.

Note: The first run on DropSolve failed. I renamed the file (not sure if the filename contributed to the problem), and tried again. Now it worked:

Margin vs Mark Up

See e.g. http://en.wikipedia.org/wiki/Gross_margin

The definitions are:

Often these terms are used in a less precise manner.

Does not happen a lot

Often Gurobi and Cplex are in the same ballpark when solving my models. But sometimes you can see something like this:

The model is related to scheduling maintenance for power generators.

Note: I also have seen cases the other way around (Gurobi much faster than Cplex).

operating on an empty set

See: http://www.johndcook.com/blog/2015/04/14/empty-sum-product/

Of course modeling systems should do this correctly.

GAMS

$onempty;
set e(*) / /;
display e;

scalars s,p;
s = sum(e,1);
p = prod(e,1);
display s,p;

Gives:

----      3 SET e 

                                                      ( EMPTY )

----      8 PARAMETER s                    =        0.000 
            PARAMETER p                    =        1.000 

AMPL

ampl: set e = {};
ampl: param s = sum{i in e} 1;
ampl: param p = prod{i in e} 1;
ampl: display s,p;
s = 0
p = 1

Diagonalization Algorithm

Following

we can write a simple diagonalization / relaxation algorithm in GAMS that computes the oligopolistic market equilibrium of the problem described here: http://yetanothermathprogrammingconsultant.blogspot.com/2015/03/oligopolistic-producer-behavior-or-why.html.

In this algorithm we solve a sub-problem where we maximize profits (varying the output) for each firm while we keep the output of the other firms constant in the sub-problem (i.e. we take them from the previous iteration of the algorithm). The sub-problem is now a straightforward NLP. It looks like:

We run this model in a loop until it converges: the quantities produced don’t change anymore:

 

We see we can reproduce the results from the paper:

----    104 PARAMETER trace               firm1       firm2       firm3       firm4       firm5        diff iter0       10.000      10.000      10.000      10.000      10.000 iter1       55.029      56.193      55.760      53.414      49.142     219.538 iter2       27.188      32.991      36.158      36.505      34.382     102.314 iter3       42.618      46.760      48.008      46.372      42.300      58.834 iter4       33.565      38.853      41.170      40.545      37.475      34.451 iter5       38.886      43.533      45.192      43.922      40.220      20.146 iter6       35.778      40.804      42.835      41.927      38.583      11.827 iter7       37.607      42.411      44.218      43.092      39.534       6.935 iter8       36.536      41.470      43.406      42.406      38.972       4.071 iter9       37.165      42.022      43.883      42.808      39.301       2.388 iter10      36.796      41.698      43.603      42.572      39.108       1.402 iter11      37.013      41.888      43.767      42.710      39.221       0.822 iter12      36.886      41.777      43.671      42.629      39.154       0.483 iter13      36.960      41.842      43.727      42.677      39.193       0.283 iter14      36.916      41.804      43.694      42.649      39.170       0.166 iter15      36.942      41.826      43.714      42.665      39.184       0.098 iter16      36.927      41.813      43.702      42.656      39.176       0.057 iter17      36.936      41.821      43.709      42.661      39.181       0.034 iter18      36.931      41.816      43.705      42.658      39.178       0.020 iter19      36.934      41.819      43.707      42.660      39.180       0.012 iter20      36.932      41.818      43.706      42.659      39.179       0.007

It is always nice to see that we can reproduce some results.

Notes:

• Note: to speed up the iterations we can set solprint and solvelink:
   
  
• Patrick Harker has been appointed as the next president of the Fed in Philadelphia [link].
• The trace output illustrates the linear convergence of this algorithm: the difference is halved by each iteration.
• This algorithm is also known as the PIES-q algorithm [link].

More fun with quadratic models

This model seems to be solving just fine:

MODEL STATISTICS BLOCKS OF EQUATIONS          81     SINGLE EQUATIONS           81 BLOCKS OF VARIABLES         127     SINGLE VARIABLES          127 NON ZERO ELEMENTS           361     NON LINEAR N-Z            240 DERIVATIVE POOL              20     CONSTANT POOL              56 CODE LENGTH                 782     DISCRETE VARIABLES         60

Gurobi           24.4.1 r50296 Released Dec 20, 2014 WEI x86 64bit/MS Windows Gurobi full license. Gurobi library version 6.0.0 Starting Gurobi... Optimize a model with 20 rows, 126 columns and 60 nonzeros Model has 60 quadratic objective terms Model has 60 quadratic constraints Coefficient statistics:   Matrix range    [1e+00, 1e+00]   Objective range [0e+00, 0e+00]   Bounds range    [5e-01, 8e+00]   RHS range       [1e+00, 1e+00] Presolve time: 0.00s Presolved: 20 rows, 126 columns, 60 nonzeros Presolved model has 60 quadratic objective terms Variable types: 66 continuous, 60 integer (60 binary) Root relaxation: objective 0.000000e+00, 41 iterations, 0.00 seconds     Nodes    |    Current Node    |     Objective Bounds      |     Work Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time H    0     0                      20.1386974    0.00000   100%     -    0s      0     0   12.95963    0    6   20.13870   12.95963  35.6%     -    0s      0     0 infeasible    0        20.13870   20.13870  0.00%     -    0s Cutting planes: Explored 0 nodes (377 simplex iterations) in 0.08 seconds Thread count was 1 (of 8 available processors) Optimal solution found (tolerance 0.00e+00) Best objective 2.013869741063e+01, best bound 2.013869741063e+01, gap 0.0% MIQCP status(2): Model was solved to optimality (subject to tolerances). Solving fixed MIQCP. Optimize a model with 20 rows, 126 columns and 60 nonzeros Model has 60 quadratic objective terms Model has 60 quadratic constraints Coefficient statistics:   Matrix range    [1e+00, 1e+00]   Objective range [0e+00, 0e+00]   Bounds range    [5e-01, 8e+00]   RHS range       [1e+00, 1e+00] Presolve removed 20 rows and 100 columns Presolve time: 0.00s Presolved: 246 rows, 260 columns, 560 nonzeros Presolved model has 60 second-order cone constraints Ordering time: 0.00s Barrier statistics: AA' NZ     : 6.030e+03 Factor NZ  : 6.276e+03 Factor Ops : 2.569e+05 (less than 1 second per iteration) Threads    : 1                   Objective                Residual Iter       Primal          Dual         Primal    Dual     Compl     Time    0   5.95174921e+02 -2.20942251e+01  5.61e+00 5.24e+00  8.70e+00     0s    1   7.73169938e+01 -9.09925343e+01  3.83e-01 5.80e-01  1.08e+00     0s    2   2.61450398e+01 -5.66216921e+00  4.50e-02 7.46e-02  1.58e-01     0s    3   2.18586349e+01  2.14234892e+00  7.66e-03 4.90e-02  9.78e-02     0s    4   2.09341242e+01  6.68994751e+00  2.23e-03 3.59e-02  7.14e-02     0s    5   2.04734405e+01  1.56421119e+01  4.98e-04 1.15e-02  2.39e-02     0s    6   2.02435139e+01  1.92199379e+01  2.82e-05 2.18e-03  4.88e-03     0s    7   2.01585476e+01  2.00900183e+01  1.20e-10 5.47e-05  2.70e-04     0s    8   2.01393068e+01  2.01370266e+01  5.85e-10 1.50e-06  8.78e-06     0s    9   2.01387075e+01  2.01386804e+01  4.13e-09 7.98e-08  9.68e-08     0s   10   2.01386974e+01  2.01386961e+01  5.47e-10 7.04e-10  4.52e-09     0s Barrier solved model in 10 iterations and 0.01 seconds Optimal objective 2.01386974e+01 Solving KKT system to obtain QCP duals... Optimize a model with 80 rows, 126 columns and 240 nonzeros Coefficient statistics:   Matrix range    [2e-03, 4e+00]   Objective range [2e-01, 2e+01]   Bounds range    [5e-01, 8e+00]   RHS range       [1e-01, 1e+01] Presolve removed 20 rows and 60 columns Presolve time: 0.02s Presolved: 60 rows, 66 columns, 180 nonzeros Ordering time: 0.00s Barrier statistics: AA' NZ     : 5.700e+02 Factor NZ  : 6.300e+02 Factor Ops : 8.610e+03 (less than 1 second per iteration) Threads    : 1                   Objective                Residual Iter       Primal          Dual         Primal    Dual     Compl     Time    0   1.64221433e+07 -1.74037374e+07  9.98e+02 5.00e+02  1.00e+06     0s    1   3.06430913e+06 -3.96880437e+06  7.86e+02 1.97e+02  4.11e+05     0s    2   7.41985462e+04 -1.37029670e+06  8.77e+01 2.58e+01  8.16e+04     0s    3   7.82357071e+02 -1.08762827e+06  5.30e+00 1.62e+00  9.72e+03     0s    4   4.89433799e+02 -5.28127121e+05  0.00e+00 1.62e-06  2.75e+03     0s    5   4.84263108e+02 -2.44700888e+03  0.00e+00 6.77e-09  1.53e+01     0s    6   1.49830346e+02 -3.22980351e+02  0.00e+00 7.99e-15  2.46e+00     0s    7   4.73122148e+01 -5.45185139e+01  0.00e+00 1.78e-15  5.30e-01     0s    8   2.37562000e+01  1.37551176e+01  0.00e+00 8.88e-16  5.21e-02     0s    9   2.03314732e+01  1.97150561e+01  0.00e+00 8.88e-16  3.21e-03     0s   10   2.01629353e+01  2.01091957e+01  0.00e+00 8.88e-16  2.80e-04     0s   11   2.01421045e+01  2.01349098e+01  0.00e+00 8.88e-16  3.75e-05     0s   12   2.01391804e+01  2.01381595e+01  0.00e+00 8.88e-16  5.32e-06     0s   13   2.01387653e+01  2.01386209e+01  0.00e+00 1.78e-15  7.53e-07     0s   14   2.01387066e+01  2.01386861e+01  0.00e+00 8.88e-16  1.07e-07     0s   15   2.01386982e+01  2.01386953e+01  0.00e+00 1.78e-15  1.51e-08     0s   16   2.01386970e+01  2.01386966e+01  0.00e+00 1.78e-15  2.14e-09     0s Barrier solved model in 16 iterations and 0.02 seconds Optimal objective 2.01386970e+01 Fixed MIQCP status(2): Model was solved to optimality (subject to tolerances). MIQCP Solution:         20.138697    (377 iterations, 0 nodes) Final Solve:            20.138697    (0 iterations) Best possible:          20.138697 Absolute gap:            0.000000 Relative gap:            0.000000

This looks all fine. Except the correct (global) optimal objective is 2.2388. The reason is: this MIQCP model is actually non-convex. Gurobi usually rejects those models (with a message about a Q matrix not being positive definite) but in this case it slips through. The solution is probably just a local optimum.

Interesting Xpress log

On a very small (convex) MIQCP model (it solves within the limits of the demo version of GAMS/Xpress) we see Xpress struggling mightily. Commercial solvers like Xpress are very robust for LP and MIP models, but they seem somewhat less reliable with respect to quadratic models, probably because they are less exposed to quadratic models.

MODEL STATISTICS BLOCKS OF EQUATIONS          51    SINGLE EQUATIONS           51 BLOCKS OF VARIABLES          89    SINGLE VARIABLES           89 NON ZERO ELEMENTS           241     NON LINEAR N-Z             80 DERIVATIVE POOL              20     CONSTANT POOL              36 CODE LENGTH                 400     DISCRETE VARIABLES         40

FICO-Xpress      24.4.1 r50296 Released Dec 20, 2014 WEI x86 64bit/MS Windows Xpress Optimizer 27.01 Xpress-Optimizer 64-bit v27.01.02 (Hyper capacity) (c) Copyright Fair Isaac Corporation 1983-2014. All rights reserved Licensed for use by: GAMS Development Corp. for GAMS Reading Problem m Problem Statistics           50 (      0 spare) rows           88 (      0 spare) structural columns          200 (      0 spare) non-zero elements           80 quadratic elements in 40 quadratic constraints Global Statistics           40 entities        0 sets        0 set members Minimizing MIQCQP m Original problem has:         50 rows           88 cols          200 elements        40 globals         40 qrows          80 qrowelem Presolved problem has:         50 rows           88 cols          200 elements        40 globals         40 qrows          80 qrowelem Will try to keep branch and bound tree memory usage below 21.7Gb Barrier cache sizes : L1=32K L2=8192K Using AVX support Cores per CPU (CORESPERCPU): 8 Barrier starts, with L2 cache 1024K Matrix ordering - Dense cols.:      0   NZ(L):       950   Flops:        14984   Its   P.inf      D.inf      U.inf      Primal obj.     Dual obj.      Compl.    0  1.91e+001  1.19e+001  9.70e+000  2.8159564e+003 -2.6134886e+002  3.8e+003    1  7.49e+000  5.91e+000  1.54e+000  5.8570174e+002 -8.3787742e+001  7.2e+002    2  1.28e+000  3.28e-001  1.10e-002  2.9030624e+000 -1.2271889e+001  1.9e+001    3  9.84e-002  1.92e-002  8.10e-004  1.6036787e-001 -1.0029935e+000  2.0e+000    4  7.98e-004  3.67e-003  5.07e-006  1.9140695e-003 -7.4258213e-003  2.5e-002    5  2.11e-006  1.03e-005  1.33e-008  5.1448073e-006 -1.5450951e-005  6.0e-005    6  2.13e-009  1.05e-008  1.34e-011  5.2140230e-009 -1.5655265e-008  6.1e-008 Barrier method finished in 0 seconds Crossover starts    Its         Obj Value      S   Ninf  Nneg        Sum Inf  Time     42           .000000      P     45     0     416.304867     0      0           .000000      N     45     0     416.304867     0      0           .000000      D     45     0        .000000     0 Crossover successful Objective function value:      .000000 time: 0      0           .000000      P     12    36       6.913862     0     14           .000000      P      0     0        .000000     0 Optimal solution found Barrier solved problem   6 barrier and 56 simplex iterations in 0s Final objective                         : 0.000000000000000e-01   Max primal violation      (abs / rel) :       0.0 /       0.0   Max dual violation        (abs / rel) :       0.0 /       0.0   Max complementarity viol. (abs / rel) :       0.0 /       0.0 All values within tolerances Starting root cutting & heuristics Its Type    BestSoln    BestBound   Sols    Add    Del     Gap     GInf   Time +           75.710978      .000000      1               75.7110        0      0 +           75.297982      .000000      2               75.2980        0      0    1  O     75.297982      .487605      2     50     20   99.35%      29      0    2  O     75.297982    13.426199      2     51     48   82.17%      26      0    3  O     75.297982    33.375760      2     38     25   55.68%      12      0    4  O     75.297982    60.087607      2     52     40   20.20%      18      0    5  O     75.297982    71.987890      2     34     40    4.40%      12      0    6  O     75.297982    74.005329      2     30     24    1.72%       6      0    7  K     75.297982    74.005329      2     13     23    1.72%      16      0    8  K     75.297982    74.005329      2      5     15    1.72%      16      0    9  K     75.297982    74.005329      2      7      5    1.72%      10      0   10  K     75.297982    74.005329      2      0      7    1.72%      10      0 Heuristic search started Heuristic search stopped Cuts in the matrix         : 73 Cut elements in the matrix : 216 Its Type    BestSoln    BestBound   Sols    Add    Del     Gap     GInf   Time    1  O     75.297982    74.005329      2     35      5    1.72%       0      0    2  O     75.297982    74.005329      2     19     36    1.72%       0      0    3  O     75.297982    74.005329      2     23     17    1.72%       0      0 Will try to keep branch and bound tree memory usage below 21.7Gb Starting tree search     Node     BestSoln    BestBound   Sols Active  Depth     Gap     GInf   Time        1    75.297982    74.005329      2      2      1    1.72%      18      0        2    75.297982    74.005329      2      1      2    1.72%      21      0        3    75.297982    74.005329      2      2      3    1.72%      20      0        4    75.297982    74.005329      2      3      4    1.72%      20      0        5    75.297982    74.005329      2      4      5    1.72%      20      0        6    75.297982    74.005329      2      5      6    1.72%      19      0        7    75.297982    74.005381      2      6      3    1.72%      19      0        8    75.297982    74.005383      2      7      7    1.72%      19      0        9    75.297982    74.031433      2      8      5    1.68%      18      0       10    75.297982    74.031433      2      9      6    1.68%      16      0 +     15    74.628262    74.031433      3     11     10    0.80%       0      0 +     19    74.628249    74.031433      4     11     14    0.80%       0      0       20    74.628249    74.031433      4     11     14    0.80%       2      0       30    74.628249    74.031433      4     18     14    0.80%       4      0       40    74.628249    74.031449      4     25     11    0.80%       8      0       50    74.628249    74.077101      4     31      8    0.74%      16      0 +     59    74.576175    74.077101      5     31     16    0.67%       0      0       60    74.576175    74.077101      5     31     16    0.67%       2      0 +     60    74.525346    74.077101      6     31     17    0.60%       0      0 B&B tree size: 144k total     Node     BestSoln    BestBound   Sols Active  Depth     Gap     GInf   Time       70    74.525346    74.077154      6     36      6    0.60%      14      0 +     79    74.501844    74.077154      7     36     14    0.57%       0      0       80    74.501844    74.077154      7     36     14    0.57%       2      0 +     80    74.451129    74.077154      8     36     15    0.50%       0      0       90    74.451129    74.079222      8     39      4    0.50%      16      0      100    74.451129    74.079222      8     45      4    0.50%      16      0      200    74.451129    74.100052      8     89     14    0.47%       6      0      300    74.451129    74.105467      8    134      9    0.46%      16      0      400    74.451129    74.123164      8    161     14    0.44%       6      0      500    74.451129    74.131429      8    185     11    0.43%       8      0      600    74.451129    74.172380      8    207     16    0.37%       2      0      700    74.451129    74.179219      8    245     10    0.37%       4      0      800    74.451129    74.203200      8    265     13    0.33%       6      0 +    884    74.441499    74.205322      9    289     20    0.32%       0      0      900    74.441499    74.205322      9    290     14    0.32%       8      0     1000    74.441499    74.205322      9    311     11    0.32%       2      0     1200    74.441499    74.205322      9    367     16    0.32%      12      0 +   1217    74.408242    74.205322     10    369     23    0.27%       0      0     1300    74.408242    74.220873     10    352     17    0.25%       4      0     1400    74.408242    74.231426     10    363     10    0.24%       8      0 B&B tree size: 1.0Mb total     Node     BestSoln    BestBound   Sols Active  Depth     Gap     GInf   Time     1500    74.408242    74.231426     10    382     16    0.24%       4      1     1700    74.408242    74.250990     10    415     14    0.21%       8      1     1800    74.408242    74.257529     10    439     15    0.20%       6      1 +   1818    74.408060    74.257529     11    436     20    0.20%       0      1     1900    74.408060    74.261403     11    443     17    0.20%       4      1     2000    74.408060    74.271531     11    448     10    0.18%       7      1     2100    74.408060    74.277093     11    451     11    0.18%       6      1     2200    74.408060    74.279215     11    462     16    0.17%       4      1     2300    74.408060    74.283948     11    468     13    0.17%       2      1     2400    74.408060    74.287506     11    477     16    0.16%       4      1     2500    74.408060    74.299222     11    468     11    0.15%       2      1     2600    74.408060    74.305186     11    477      7    0.14%      10      1     2700    74.408060    74.305319     11    485     14    0.14%       8      1     2800    74.408060    74.305319     11    479     15    0.14%       4      1     3000    74.408060    74.315007     11    449     16    0.13%       4      1     3100    74.408060    74.327330     11    427     17    0.11%       4      2     3200    74.408060    74.331422     11    420     15    0.10%       2      2     3400    74.408060    74.342707     11    377     13    0.09%       8      2     3500    74.408060    74.352660     11    363     15    0.07%       2      2     3600    74.408060    74.359277     11    339     19    0.07%       4      2 B&B tree size: 1.3Mb total     Node     BestSoln    BestBound   Sols Active  Depth     Gap     GInf   Time     3700    74.408060    74.373115     11    303     13    0.05%       2      2     3900    74.408060    74.379200     11    275     15    0.04%       4      2     4000    74.408060    74.379212     11    258     14    0.04%       2      2     4200    74.408060    74.387502     11    192     19    0.03%       5      2     4500    74.408060    74.405315     11     59     15   0.004%       4      3     4600    74.408060    74.405640     11     15     15   0.003%      10      3 *** Search completed ***     Time:     3 Nodes:       4629 Number of integer feasible solutions found is 11 Best integer solution found is    74.408060 Best bound is    74.408060 Warning: 6 node(s) could not be solved or branched. Final bound or status may be incorrect. Uncrunching matrix fixing discrete vars and re-solving as an LP. Minimizing QCQP m Original problem has:         50 rows           88 cols          200 elements         40 qrows          80 qrowelem Presolved problem has:         40 rows           48 cols          120 elements         40 qrows          80 qrowelem Barrier cache sizes : L1=32K L2=8192K Using AVX support Cores per CPU (CORESPERCPU): 8 Barrier starts, with L2 cache 1024K Matrix ordering - Dense cols.:      0   NZ(L):       376   Flops:         2520   Its   P.inf      D.inf      U.inf      Primal obj.     Dual obj.      Compl.    0  1.83e+001  2.52e+001  1.16e+001  1.5112915e+003 -9.4937458e+002  2.6e+003    1  4.74e+000  9.55e+000  1.19e+000  2.5408247e+002 -2.9217970e+002  3.9e+002    2  2.34e+000  3.44e+000  3.35e-001  7.8404847e+001 -1.0977438e+002  1.4e+002    3  7.92e-001  6.84e-001  1.89e-002  5.2158577e+000 -1.3750171e+001  1.4e+001    4  6.28e-001  6.38e-001  1.33e-002  4.1020675e+000 -7.8600545e+000  1.1e+001    5  4.37e-001  3.32e-001  8.43e-003  9.0795149e+000  3.4120483e-001  1.5e+001    6  1.98e-001  2.61e-001  3.73e-003  9.3869573e+000  4.9561739e+000  8.6e+000    7  3.63e-002  6.02e-002  3.74e-004  8.7705271e+000  7.9879673e+000  1.3e+000    8  8.70e-003  2.50e-002  3.59e-005  8.6114463e+000  8.6224795e+000  1.4e-001    9  2.28e-003  1.31e-002  4.91e-006  8.5979647e+000  8.6831580e+000  2.5e-002   10  3.52e-004  2.47e-003  4.60e-009  8.5944005e+000  8.5952389e+000  2.2e-004   11  5.07e-005  7.03e-004  6.92e-012  8.5943916e+000  8.5948297e+000  2.1e-005   12  8.59e-006  2.20e-004  8.78e-016  8.5943913e+000  8.5944862e+000  2.5e-006   13  1.56e-006  7.24e-005  8.78e-016  8.5943913e+000  8.5944094e+000  2.9e-007   14  3.00e-007  2.42e-005  1.10e-015  8.5943913e+000  8.5943941e+000  3.3e-008 Barrier method finished in 0 seconds Uncrunching matrix Optimal solution found    Its         Obj Value      S   Ninf  Nneg        Sum Inf  Time      0          8.594391      B      0     0        .000000     0 Barrier solved problem   14 barrier iterations in 0s Final objective                         : 8.594391251039179e+00   Max primal violation      (abs / rel) : 8.474e-07 / 5.042e-08   Max dual violation        (abs / rel) :       0.0 /       0.0   Max complementarity viol. (abs / rel) : 4.300e-07 / 1.758e-08 All values within tolerances fixed LP solved successfully, objective = 8.59439125104. Integer solution proven optimal. MIP solution  :          8.594391 Best possible :         74.408060 Absolute gap  :        -65.813669     optca :          0.000000 Relative gap  :         -0.884497     optcr :          0.000000

The correct optimal objective is 0.8404.