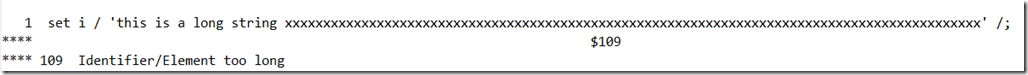Yet Another Math Programming Consultant: May 2013

Friday, May 31, 2013

Large Scale Aggregation Example

Teaching a course about GAMS modeling as USDA. A large real-world aggregation step cannot be ommitted! Here is an example how we can do many things in one step:

Even though the raw data was too large to fit into Excel, GAMS aggregates this very quickly: < 2 seconds.

Wednesday, May 22, 2013

Data Models and Optimization Models

Just had another example of what I see more often. In this case we deal with a fairly small data model. Unfortunately the db guru has mixed up flow and stock variables. When developing a scheduling model the difference between a time period and a point in time is rather important, and I need to explicitly deal with this in the model. The concept of time seems often to be misunderstood.

In this case, I tried to raise the issue but the db people became defensive and angry, so I dropped it quickly. In such a situation it is best to make some reasonable assumptions (e.g. about if something is measured at the beginning or the end of a time period) and be prepared to change the model when the first results are presented.

More general: there is much more hand waiving possible in db design than in the implementation of optimization models. We often have to be much more precise even (may be especially) if the db design is beautifully documented with all kind of fancy diagrams (these sometimes give a false impression of precision).

Another observation that further strengthens this argument that in almost all cases data from a database contains errors. As optimization models typically see the whole thing ("simultaneous equations") we often see errors in the data that were never observed by the db people. Referential integrity goes only so far....

Fodder

I am teaching an Intro GAMS class at a government agency, and I was thinking about doing a shortest path model as LP. There are lots of interesting angles from a modeling perspective, at least I think so. I can talk easily for an hour or more just about that. But now I read this is all just fodder:

Given a directed graph (V, A) with source node s, target node t, and cost w_ij for each arc (i, j) in A, consider the program with variables x_ij

minimize $\sum_{ij \in A} w_{ij} x_{ij}$ subject to $x \ge 0$ and for all i, $\sum_j x_{ij} - \sum_j x_{ji} = \begin{cases}1, &\text{if }i=s;\\ -1, &\text{if }i=t;\\ 0, &\text{ otherwise.}\end{cases}$

This LP, which is common fodder for operations research courses, has the special property that it is integral

http://en.wikipedia.org/wiki/Shortest_path_problem

In my opinion there are quite a few things to say about modeling these things (even without discussing algorithms at all):

Dense vs. sparse
How to prevent inadmissible arcs to show up in the solution (high cost, fix to zero, don't generate those at all)
One-directional, bi-directional arcs
Large networks
Data input

The appeal of this model is one does not have explain a lot about the problem itself.

Monday, May 20, 2013

Elements of Statistical Learning

Although the book is available as PDF file from http://www-stat.stanford.edu/~tibs/ElemStatLearn/ I decided to spend the $80 and ordered the book as real book. It was delivered this weekend. Some beautiful graphs and pictures: highly recommended.

Interesting quote (italics by me):

Often neural networks have too many weights and will overfit the data at the global minimum of R. In early developments of neural networks, either by design or by accident, an early stopping rule was used to avoid overfitting. Here we train the model only for a while, and stop well before we approach the global minimum.

Friday, May 17, 2013

Visualization of Model Results

I was working on some sheets about visualization of results of policy models. Of course we cannot leave out Hans Rosling:

Microsoft Update

Critical Information Regarding Microsoft Update and ArcGIS

A recent Microsoft update (deployed as KB 2732673, KB 2775511, or KB 2824408) may result in data corruption when using ArcGIS on a Windows 7 system and writing data to remote data storage on a Windows Vista, 7, 2008/2008 R2, or 2012 system. This data corruption appears as truncation of a write request and has shown up in file geodatabases and shapefiles.

Microsoft has acknowledged the problem, identified the affected component as RDBSS.sys, and provided
further details.

Esri and Microsoft are working closely to understand what has changed in the RDBSS.sys component and
how to resolve the problem.

Microsoft recommends not installing the above-referenced updates.

See Esri Knowledge Base article 41119 for further information and updates.

Oops…

Thursday, May 16, 2013

Long Strings

Should developers impose hard limits on lengths of strings?

Yesterday struggled good part of the day to work around some issues where we needed long labels in GAMS. Looking back I think that in general systems should not impose such limits if at all possible. Any such limit is rather artificial anyway, and there are always cases where they become a problem.

Quantum Computing vs Cplex

http://graphics8.nytimes.com/packages/pdf/business/quantum-study.pdf

Summary: on some exotic hardware we can find good solutions (heuristic) for some combinatorial problems much faster than with Cplex on standard hardware.

I am not familiar with what is this really is. Some more information is here:

Wikipedia entry: http://en.wikipedia.org/wiki/D-Wave_Systems (the picture below is also from Wikidepia).
Company web-site: http://www.dwavesys.com/en/dw_homepage.html
In-depth blog posting: http://www.scottaaronson.com/blog/?p=1400
More blogs postings: http://mat.tepper.cmu.edu/blog/?p=1786, https://www.ibm.com/developerworks/community/blogs/jfp/entry/will_quantum_computing_kill_cplex
USC paper: http://arxiv.org/abs/1304.4595
The Economist! http://www.economist.com/news/science-and-technology/21578027-first-real-world-contests-between-quantum-computers-and-standard-ones-faster

Photograph of a chip constructed by D-Wave Systems Inc. designed to operate as a 128-qubit superconducting adiabatic quantum optimization processor, mounted in a sample holder. (Source: Wikipedia)
Note: the paper is located at the NY Times?

PS: the box is a bit larger than I expected:

Tuesday, May 14, 2013

Scalar models: CP models in AMPL

AMPL has since a long time facilities to write Constraint Programming models (see http://users.iems.northwestern.edu/~4er/WRITINGS/cp.pdf), but only recently this became available for the general public. In http://www.hakank.org/ampl/ there is a nice collection of CP models written in AMPL. Very worthwhile to have a look if you want to write CP models in AMPL.
Of course I always have a few minor beefs with how models are written. Here is the first model:

/*

  "A puzzle" in AMPL+CP.

  From "God plays dice"
  "A puzzle"
  http://gottwurfelt.wordpress.com/2012/02/22/a-puzzle/
  And the sequel "Answer to a puzzle"
  http://gottwurfelt.wordpress.com/2012/02/24/an-answer-to-a-puzzle/

  This problem instance was taken from the latter blog post.
  """
  8809 = 6
  7111 = 0
  2172 = 0
  6666 = 4
  1111 = 0
  3213 = 0
  7662 = 2
  9312 = 1
  0000 = 4
  2222 = 0
  3333 = 0
  5555 = 0
  8193 = 3
  8096 = 5
  7777 = 0
  9999 = 4
  7756 = 1
  6855 = 3
  9881 = 5
  5531 = 0

  2581 = ?
  """

  Note: 
  This model yields 10 solutions, since x4 is not 
  restricted in the constraints. 
  All solutions has x assigned to the correct result. 
  

  The problem stated in "A puzzle"
  http://gottwurfelt.wordpress.com/2012/02/22/a-puzzle/
  is
  """
  8809 = 6
  7662 = 2
  9312 = 1
  8193 = 3
  8096 = 5
  7756 = 1
  6855 = 3
  9881 = 5

  2581 = ?
  """
  This problem instance - using the same principle - yields 
  two different solutions of x, one is the same (correct) as 
  for the above problem instance, and one is not.
  This is because here both x4 and x1 are underdefined.
  

  Note: 
  This problem has another non-algebraic and - let us say - topological
  approach which yield the same solution as the first problem and one
  of the solutions of the second problem.


  This AMPL model was created by Hakan Kjellerstrand, hakank@gmail.com
  See also my AMPL page: http://www.hakank.org/ampl/

*/

param n;

# decision variables
var x0 >= 0 <= 9 integer;
var x1 >= 0 <= 9 integer;
var x2 >= 0 <= 9 integer;
var x3 >= 0 <= 9 integer;
var x4 >= 0 <= 9 integer;
var x5 >= 0 <= 9 integer;
var x6 >= 0 <= 9 integer;
var x7 >= 0 <= 9 integer;
var x8 >= 0 <= 9 integer;
var x9 >= 0 <= 9 integer;

var x >= 0 <= 9 integer;

#
# constraints
#
s.t. c1:
  x8+x8+x0+x9 = 6 and
  x7+x1+x1+x1 = 0 and
  x2+x1+x7+x2 = 0 and
  x6+x6+x6+x6 = 4 and
  x1+x1+x1+x1 = 0 and
  x3+x2+x1+x3 = 0 and
  x7+x6+x6+x2 = 2 and
  x9+x3+x1+x2 = 1 and
  x0+x0+x0+x0 = 4 and
  x2+x2+x2+x2 = 0 and
  x3+x3+x3+x3 = 0 and
  x5+x5+x5+x5 = 0 and
  x8+x1+x9+x3 = 3 and
  x8+x0+x9+x6 = 5 and
  x7+x7+x7+x7 = 0 and
  x9+x9+x9+x9 = 4 and
  x7+x7+x5+x6 = 1 and
  x6+x8+x5+x5 = 3 and
  x9+x8+x8+x1 = 5 and
  x5+x5+x3+x1 = 0 and

  x2+x5+x8+x1 = x
;

# This smaller variant yields two different values for x.
# s.t. c2:
#  x8+x8+x0+x9 = 6 and
#  x7+x6+x6+x2 = 2 and
#  x9+x3+x1+x2 = 1 and
#  x8+x1+x9+x3 = 3 and
#  x8+x0+x9+x6 = 5 and
#  x7+x7+x5+x6 = 1 and
#  x6+x8+x5+x5 = 3 and
#  x9+x8+x8+x1 = 5 and

#  x2+x5+x8+x1 = x
# ;

data;


# option presolve 0;
option show_stats 2;

option solver gecode;
option gecode_options "var_branching=size_min val_branching=min outlev=1 outfreq=1";

# option solver ilogcp;
# option ilogcp_options "optimizer=cp alldiffinferencelevel=4 debugexpr=0 logperiod=10 logverbosity=0";

solve;

display x;
display x0,x1,x2,x3,x4,x5,x6,x7,x8,x9;

The first thing we notice is that the model is written using scalar variables and equations. We are not using the indexing facilities of AMPL although variable names like x0,x1,x2, suggest we could exploit indexing.

The one big equation is really a set of equations. If we write a set of simultaneous equations this is really like we use the AND operator in between the equations.

The different data sets are formulated as different models. It make sense to ask: “can we write this as one and the same model with just different data?”. I.e. we want to make the model data driven. Of course we want to keep the model structure. If our only goal was to make the model 100% data drive we just could formulate Ax=b and we are done. But such a model is not at the correct abstraction level, and moves all the complexity to the correct organization of the data. If you ever used the Matlab solvers from the Optimization Toolbox you know what I am talking about. We definitely want to convey the structure and purpose of the model inside the AMPL model (that is why modeling systems have been developed). Here is my attempt:

Model

 
set R;   # number of records in training set
set P;   # data record

param raw {R,P};  # raw data

set I = 0..9;   # x{I} variables

set Px := P diff {'y'};
param datax {r in R, i in I} = sum{p in Px: raw[r,p]=i} 1;


var x{I} >=0 <=9 integer;
var y >=0 <=9 integer;

s.t. e{r in R diff {'r0'}}:
    sum{i in I} datax[r,i] * x[i] = raw[r,'y'];

s.t. ydef:
     y = sum{i in I} datax['r0',i] * x[i];

Data set 1


set R := r0 r1 r2 r3 r4 r5 r6 r7 r8 r9 r10 r11 r12 r13 r14 r15 r16 r17 r18 r19 r20;
set P := c1 c2 c3 c4 y;
param raw: c1 c2 c3 c4 y :=
  r0  2  5  8  1  .
  r1  8  8  0  9  6
  r2  7  1  1  1  0
  r3  2  1  7  2  0
  r4  6  6  6  6  4
  r5  1  1  1  1  0
  r6  3  2  1  3  0
  r7  7  6  6  2  2
  r8  9  3  1  2  1
  r9  0  0  0  0  4
  r10 2  2  2  2  0
  r11 3  3  3  3  0
  r12 5  5  5  5  0
  r13 8  1  9  3  3
  r14 8  0  9  6  5
  r15 7  7  7  7  0
  r16 9  9  9  9  4
  r17 7  7  5  6  1
  r18 6  8  5  5  3
  r19 9  8  8  1  5
  r20 5  5  3  1  0
;

Data set 2


set R := r0 r1 r2 r3 r4 r5 r6 r7 r8;
set P := c1 c2 c3 c4 y;
param raw: c1 c2 c3 c4 y :=
  r0  2  5  8  1  .
  r1  8  8  0  9  6
  r2  7  6  6  2  2
  r3  9  3  1  2  1
  r4  8  1  9  3  3
  r5  8  0  9  6  5
  r6  7  7  5  6  1
  r7  6  8  5  5  3
  r8  9  8  8  1  5
;

This can now be solved with any CP and MIP solver. As we can see the model is now a little bit more complex but more compact compared to the scalar model.

Note: In many cases it is possible to let AMPL extract the driving sets from a parameter in a data file. I believe this is not possible in this case where we use a tabular notation. That means we have to form the sets R and P explicitly. It would have been helpful if we could have used something like set R := r0..r8; but that is not something that is supported by AMPL.

Wednesday, May 8, 2013

Sparse matrix multiplication in SQL

This actually could work reasonably well:

Source: http://research.microsoft.com/en-us/um/redmond/events/escience2012/Bill_Howe.pdf