Option optcr

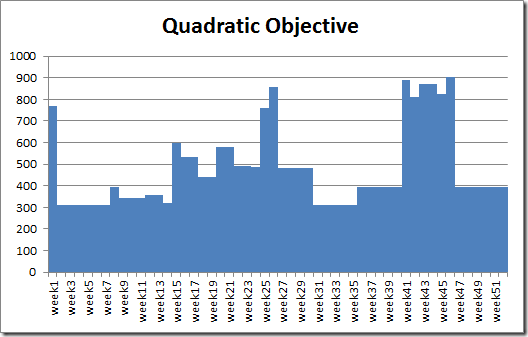
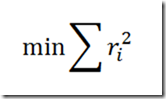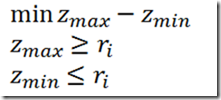Some of the MIP models in http://www.amazon.com/gp/product/0471150436 (these models are written in GAMS) seem to be missing OPTION OPTCR=0, so some non-optimal solutions are presented. By default GAMS uses a 10% relative gap criterion.

E.g.:

But I see:

Next month teaching a GAMS course in Germany. I’ll be sure to mention this (and how to spot this in the listing file).

GAMS is quite unique in having a default with nonzero gap optimality criteria. Other systems typically like to solve to optimality unless instructed otherwise.

PS. See comment for another system with a nonzero gap tolerance.

Cplex 12.5 vs 12.4 Out of memory handling

With Cplex 12.4:

Besides Cplex crashing here, we also see poor error recovery and exception handling by the calling problem. It is good to see that with Cplex 12.5 we see much better behavior:

This is with 32 bit software. We could use a 64-bit version instead to allow larger memories, but instead I opted for reformulating the model and making it smaller so I don’t leave this work to the presolver.

Better element names

Sometimes I see GAMS code like:

SETS
  K index of periods of time  /1*4/
  J index of generators /1*3/

In general I don’t like plain numbers as set elements. I prefer something like:

SETS
  K index of periods of time  /t1*t4/
  J index of generators /gen1*gen3/

This often improves the readability of the output. This is especially the case in the GDX viewer where we can swap rows and columns. Here is a some sample output:

Numerical	Id+Numerical
SETS   K index of periods of time  /1*4/   J index of generators /1*3/	SETS   K index of periods of time  /t1*t4/   J index of generators /gen1*gen3/
----    110 VARIABLE p.L  output power of generator j at period k               2           3           4   1     150.000     350.000     260.000 2                 100.000 3                  50.000     140.000	----    110 VARIABLE p.L  output power of generator j at period k                 t2          t3          t4   gen1     150.000     350.000     260.000 gen2                 100.000 gen3                  50.000     140.000

For this small example this is not terribly convincing, but for larger, high-dimensional data it surely helps in understanding output quickly.

Lazy Constraints and GAMS

> Can I use lazy constraints in my GAMS model?

Sorry, the answer is “no”. Lazy constraints are supported by the Cplex and Gurobi solvers. Other modeling systems (AMPL, AIMMS) support lazy constraints, but GAMS does not. There have been some attempts to implement this in GAMS but they were not useable in practice (using scalar models as intermediary). This was more for testing I think. 

Here is a discussion on lazy constraints: http://orinanobworld.blogspot.com/2012/08/user-cuts-versus-lazy-constraints.html

Long SQL queries

Over the holidays I ran a small script against SQL Server. Basically spatial queries. I ran the script in pieces to make sure I did not have to rerun the whole thing if something went wrong. That was a good idea: some of the queries took 6 or 7 hours or more. With memories getting larger, may be tasks like this are better done in-core than using a database. 

No error message

I have posted regularly about poor error messages from software. In general I find that the importance of formulating meaningful  error messages is underestimated by developers, leading to some level of frustration by users. Of course, issuing no error message at all is even easier for a developer (and even more difficult for users to deal with).

S O L V E      S U M M A R Y      MODEL   LANDfeas            OBJECTIVE  totallow      TYPE    LP                  DIRECTION  MINIMIZE      SOLVER  MOSEK               FROM LINE  165233 **** SOLVER STATUS     4 Terminated By Solver      **** MODEL STATUS      14 No Solution Returned     **** OBJECTIVE VALUE                0.0000 RESOURCE USAGE, LIMIT         20.311    900000.000 ITERATION COUNT, LIMIT         0        900000     Copyright (C)   MOSEK ApS, Fruebjergvej 3, Box 16                     DK-2100 Copenhagen, Denmark                     http://www.mosek.com GAMS/MOSEK Extended license detected No solution returned

I received a listing file with this fragment. I have no idea how I can help the user as I have no idea what went wrong. Now I need to get the model and data files and see if I can reproduce the problem. We see some strange trade-offs at work here: the developers saved some time by not providing code to print a readable message, and as a result (multiple) users have to spent extra time and effort in supporting and maintaining an application.

MySQL and union

For a GAMS model I need to read data from a MySQL database. Some of the data can be easily imported into a GAMS gdx file using an SQL UNION construct:

SELECT id,xxx FROM tableA
UNION
SELECT `obj’,xxx FROM tableB

Now the interesting part is that ids are INTs. So basically the first column looks like

1	xxx
2	xxx
3	xxx
obj	xxx

On my MySQL installation, the first column gets a correct type of VARCHAR(11) as the integer type was INT(10) – the extra char is for the sign I think (although we have only positive ids). However when the client was testing this, it went terribly wrong. Turned out that their MySQL version created a type of VARBINARY(11), a BLOB like type. This created havoc downstream. Luckily I was using $LOADDC in GAMS to read the GDX file produced by SQL2GMS, so we caught a domain error.

No doubt this was bad SQL produced by me. I tried something similar with SQL Server, and SQL Server complains directly about not being able to put a string into integer type. The fix: using a cast as in:

SELECT cast(id as char(10)),xxx FROM tableA
UNION
SELECT `obj’,xxx FROM tableB

A little bit troublesome that different versions of MySQL behave differently on this.

Fun with SQL Server and Quotes

I am trying to help with some SQL and we were really having fun today! A complicated dynamic SQL statement involving cursors was failing with the illuminating error: syntax error near ‘a’. When working with SQL Server it is not easy to parameterize for table names, hence the dynamic SQL instead of normal static SQL. Well, the problem turned out to be a quote in a name in the database. This was causing the generated SQL statement to be incorrect.

The best would be to fix all SQL queries, but that was not feasible right now. Instead we tried to replace all quotes by two quotes. (This was a staging table anyway, so no problem in polluting this table: it is not used by others). Sometimes you have to be pragmatic and take a short cut. The static SQL to do: replace a single quote by two single quotes looks already funky but the dynamic SQL version is really horrific:

Low cost parallel computing

There are a few interesting projects going on:

• Raspberry Pi + Lego based “supercomputer”: http://www.southampton.ac.uk/~sjc/raspberrypi/. It is estimated you need 1.4 million Raspis (and a lot of Lego) to build a machine that appears in the TOP500 of supercomputers (http://hackaday.com/2012/09/12/64-rasberry-pis-turned-into-a-supercomputer/).
• Adepteva (http://www.adapteva.com/) is working on a $99 board including some 16 parallel RISC coprocessor cores. “A cluster of 100 16-core Parallellas would cost $10,000 and provide 10 teraflops” (http://arstechnica.com/information-technology/2012/09/99-raspberry-pi-sized-supercomputer-touted-in-kickstarter-project/).

History of LP/MIP

http://www.gurobi.com/pdf/a-brief-history-of-optimization.pdf. I am always fascinated by these stories… Every time when looking back I am impressed by the size and complexity of models we can solve these days on our laptops compared to what we could solve on mainframes and supercomputers a few decades ago (and with much more convenience).

PS. You also may want to look at the whole issue at: http://www.zib.de/groetschel/publications/OptimizationStories.pdf. More interesting historic details about optimization.

GAMS question

A question was posed at https://groups.google.com/forum/?fromgroups=#!topic/gamsworld/0qYEcVd9x8I:

set    j  /n1*n5/,        k  /n5/; variable pi(j); scalar ab; ab=sum (k, sum(j$(ord(j)=ord(k)), pi.L(j) )  );

The user want to pick the 5-th element. This implementation clearly does not work. Some valid answers were given:

Ab= sum(j$sameas(j,“n5“), pi.L(j) )  ; or ab=sum (k, sum(j$sameas(j,k), pi.L(j) )  );

However I would say this is not really good modeling practice. The best approach IMHO would be:

set   j     /n1*n5/,       k(j)  /n5/; variable pi(j); scalar ab; ab=sum(k, pi.L(k));

There are two advantages of this approach:

• The set k is now domain checked against j; no elements outside j can be specified here without alarm bells going off. Domain checking is very important when developing large, complex models.
• We can substantially simplify the assignment to ab and increase readability. The expression conveys immediately what it is supposed to do.

Setting up proper subsets will help you down the road.

Parallel LP

> Can I run LP solver in parallel on multiple cores? What about all running on GPUs?

All major LP solvers include a barrier/interior point code that can run on multiple cores. This includes Cplex, Gurobi and Mosek. Do not expect perfect scaling but some speed-up is possible. Sparse simplex algorithms are not ideally suited for parallelization. Some recent results were shown by John Forrest. See: ISMP 2012 talk.

About GPUs:

(From the same talk).

There are some other algorithms that can be implemented on GPUs. Many meta-heuristics have been ported to these devices. Here are some links:

• http://www.fit.vutbr.cz/research/view_pub.php?file=%2Fpub%2F9184%2F60240442.pdf&id=9184
• http://link.springer.com/chapter/10.1007%2F978-3-642-04843-2_4?LI=true
• http://www.gputechconf.com/content/GTC/posters/2010/A04-Parallel-Ant-Colony-Optimization-with-CUDA.pdf
• http://sikaman.dyndns.org:8888/honours/karim-tantawy-winter-2011.pdf
• and many more

Don’t always trust what a solver is saying

This is supposed to be a fairly difficult MIQP. However, when I run it I get quickly: INFEASIBLE:

Tried aggregator 2 times. MIQP Presolve eliminated 1 rows and 1 columns. MIQP Presolve modified 248 coefficients. Aggregator did 52 substitutions. Reduced MIQP has 125 rows, 548 columns, and 3696 nonzeros. Reduced MIQP has 496 binaries, 0 generals, 0 SOSs, and 0 indicators. Reduced MIQP objective Q matrix has 52 nonzeros. Presolve time =    0.00 sec. Probing time =    0.00 sec. Clique table members: 654. MIP emphasis: balance optimality and feasibility. MIP search method: dynamic search. Parallel mode: none, using 1 thread. Tried aggregator 1 time. No QP presolve or aggregator reductions. Presolve time =    0.00 sec. Parallel mode: none, using 1 thread for barrier Number of nonzeros in lower triangle of A*A' = 2360 Using Approximate Minimum Degree ordering Total time for automatic ordering = 0.00 sec. Summary statistics for Cholesky factor:   Rows in Factor            = 125   Integer space required    = 241   Total non-zeros in factor = 3007   Total FP ops to factor    = 90075 Itn      Primal Obj        Dual Obj  Prim Inf Upper Inf  Dual Inf             0  1.4172319e+007 -1.4172911e+007 2.45e+003 5.04e+002 2.77e+007    1  1.2037355e+007  1.0009350e+007 1.78e+002 3.66e+001 2.01e+006    2  1.1903244e+007  1.1658232e+007 2.15e+001 4.42e+000 2.43e+005    3  1.1888608e+007  1.1839300e+007 4.33e+000 8.90e-001 4.89e+004    4  1.1885153e+007  1.1882071e+007 2.71e-001 5.56e-002 3.05e+003    5  1.1884924e+007  1.1884909e+007 1.33e-003 2.73e-004 1.50e+001 Barrier time =    0.05 sec. Total time on 1 threads =    0.05 sec. Root relaxation solution time =    0.05 sec.         Nodes                                         Cuts/    Node  Left     Objective  IInf  Best Integer    Best Bound    ItCnt     Gap       0     0    infeasible                                          5         Root node processing (before b&c):   Real time             =    0.05 Sequential b&c:   Real time             =    0.00                           ------- Total (root+branch&cut) =    0.05 sec. MIQP status(119): integer infeasible or unbounded Problem is integer infeasible. **** SOLVER STATUS     1 Normal Completion         **** MODEL STATUS      10 Integer Infeasible       **** OBJECTIVE VALUE               NA

OK, but that sounds not really correct. I found a good integer solution with a linearized objective (same constraints). So lets fix the integer variables and see what happens:

* solve MIP
solve gms1 minimizing z using mip;
* fix integer variables
x.fx(i,t) = x.l(i,t);
* and feed it into MIQP solver
solve gms2 minimizing z using miqcp;

Now I see:

Tried aggregator 1 time. MIQP Presolve eliminated 178 rows and 601 columns. All rows and columns eliminated. Presolve time =    0.00 sec. MIQP status(101): integer optimal solution Fixing integer variables, and solving final QP.. Tried aggregator 1 time. QP Presolve eliminated 178 rows and 601 columns. All rows and columns eliminated. Presolve time =    0.00 sec. Total time on 1 threads =    0.00 sec. QP status(1): optimal Proven optimal solution. MIP Solution:     14817439.000000    (0 iterations, 0 nodes) Final Solve:      14817439.000000    (0 iterations)

Hmm, so not integer infeasible after all. Some more experiments yielded:

• Using MIPSTART with the MIP solution allowed the MIQP solver to proceed
• Scaling the objective cause the MIQP to proceed also. The scaling looks like:
  objective2.. z =e= sum(t,sqr(reserves(t)))/1e6;

Don’t always trust the messages from the solvers…

GAMS qp interface not very coherent

It is possible to write quadratically constrained problems (and QPs in particular) in GAMS and solve them efficiently with solvers like Cplex, Gurobi. But the rules are somewhat ad-hoc and incoherent.

1. GAMS will not extract a QCP when using the notation x**2 (for a rather obscure reason; this should probably be dealt with in a smarter way)
2. GAMS will extract a QCP with the notation x*x or sqr(x) or power(x,2)
3. But GAMS will again not allow power(x,1) or power(x,0) so we can’t write the following:

sets   g 'generators' /g1,g2/   d 'degree'   /d0,d1,d2/ ; table cfuelcost(g,d)  'coefficients for fuel cost as quadratic function of output.'       d2        d1       d0 g1    0.00889   10.333   200 g2    0.00741   10.833   240 ; parameter v(d); v(d) = ord(d)-1; variables    p(g)      'output'    fuelcost  'total fuel cost' ; positive variable p; equations    efuel    'fuel consumption constraint' ; * power(x,2) is allowed * power(x,1) or power(x,0) is not recognized????? *efuel.. fuelcost =e= sum(g, cfuelcost(g,'d2')*power(p(g),2) + cfuelcost(g,'d1')*p(g) + cfuelcost(g,'d0')); efuel.. fuelcost =e= sum((g,d), cfuelcost(g,d)*power(p(g),v(d))); model m /all/; option qcp=cplex; solve m using qcp minimizing fuelcost;

In forbidden cases you’ll get the poorly worded error message:

*** Could not load data from file: Detected 1 general nonlinear rows in model

Smoothing

In a scheduling model for maintenance of power generators the objective is to smooth the reserves. The authors use a quadratic objective to model and the results over a year look like:

  

MIQP’s still solve significantly slower than MIP models, so I was looking for a linear approximation. The first thing that comes to mind is to minimize the max. This gives:

The problem here is we get a few weeks with really low reserves. An alternative is to minimize the difference between the max and the min. This looks like:

This actually looks quite similar to the first picture, and we have achieved our goal: make the model linear.

1 vs 4 threads

Running a small MIP using 1 thread:

Optimize a model with 177 rows, 549 columns and 3800 nonzeros Presolve time: 0.02s Presolved: 177 rows, 549 columns, 3944 nonzeros Variable types: 1 continuous, 548 integer (496 binary) Found heuristic solution: objective 949.0000000 Root relaxation: objective 4.990000e+02, 947 iterations, 0.03 seconds     Nodes    |    Current Node    |     Objective Bounds      |     Work Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time      0     0  499.00000    0   63  949.00000  499.00000  47.4%     -    0s      0     0  499.00000    0   93  949.00000  499.00000  47.4%     -    0s      0     0  499.00000    0   63  949.00000  499.00000  47.4%     -    0s      0     2  499.00000    0   63  949.00000  499.00000  47.4%     -    0s H  135   117                     910.0000000  499.00000  45.2%  47.3    0s *  204    96              44     901.0000000  499.00000  44.6%  47.1    0s   1963   797  891.00000   34   53  901.00000  578.12129  35.8%  46.1    5s   6122  2135  822.02658   39   78  901.00000  720.84013  20.0%  34.5   10s  12502  3801     cutoff   44       901.00000  796.00000  11.7%  27.4   15s  21404  5575  891.00000   51   42  901.00000  862.00000  4.33%  21.7   20s  34494  6391  891.00000   42   53  901.00000  891.00000  1.11%  17.1   25s  52100  4430  891.00000   67   60  901.00000  891.00000  1.11%  12.8   31s  68445  3439     cutoff   72       901.00000  891.00000  1.11%  10.7   35s  94101  2702 infeasible   56       901.00000  891.00000  1.11%   8.9   40s 115791  2055     cutoff   55       901.00000  891.00000  1.11%   8.0   45s 141811  1165  891.00000   40   81  901.00000  891.00000  1.11%   7.2   50s 168722   165  891.00000   44   59  901.00000  891.00000  1.11%   6.7   55s Explored 177443 nodes (1164346 simplex iterations) in 56.54 seconds Thread count was 1 (of 8 available processors) Optimal solution found (tolerance 0.00e+00) Best objective 9.010000000000e+02, best bound 9.010000000000e+02, gap 0.0% MIP status(2): Model was solved to optimality (subject to tolerances).

Now solve the same model with the same solver on the same machine using 4 threads:

Optimize a model with 177 rows, 549 columns and 3800 nonzeros Presolve time: 0.02s Presolved: 177 rows, 549 columns, 3944 nonzeros Variable types: 1 continuous, 548 integer (496 binary) Found heuristic solution: objective 949.0000000 Root relaxation: objective 4.990000e+02, 947 iterations, 0.03 seconds     Nodes    |    Current Node    |     Objective Bounds      |     Work Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time      0     0  499.00000    0   63  949.00000  499.00000  47.4%     -    0s      0     0  499.00000    0   93  949.00000  499.00000  47.4%     -    0s      0     0  499.00000    0   63  949.00000  499.00000  47.4%     -    0s      0     3  499.00000    0   63  949.00000  499.00000  47.4%     -    0s *  141    97              50     901.0000000  499.00000  44.6%  50.9    0s   6876  3503     cutoff   64       901.00000  558.96236  38.0%  30.4    5s  31149  7878 infeasible   58       901.00000  891.00000  1.11%  18.1   10s  72874  4957     cutoff   63       901.00000  891.00000  1.11%  12.2   18s  87864  4665  891.00000   55    8  901.00000  891.00000  1.11%  11.3   20s . . . . 97009933 49020  897.00000   80   47  901.00000  897.00000  0.44%   5.8 9085s 97054184 47405 infeasible   86       901.00000  897.00000  0.44%   5.8 9090s 97103347 45433 infeasible   95       901.00000  897.00000  0.44%   5.8 9095s 97174397    76 infeasible   97       901.00000  900.91810  0.01%   5.8 9100s Explored 97174474 nodes (560614904 simplex iterations) in 9100.06 seconds Thread count was 4 (of 8 available processors) Optimal solution found (tolerance 0.00e+00) Best objective 9.010000000000e+02, best bound 9.010000000000e+02, gap 0.0% MIP status(2): Model was solved to optimality (subject to tolerances).

Solution times go from 1 minute to 2.5 hours! Extrapolating this to 8 cores gives me the shivers….

Data errors

Even small tables can contain errors. An example data set in a published paper about scheduling maintenance of power generators looks like:

In GAMS I transcribed this as:

table data(i,*)            capacity   allowed-from  allowed-to  outage-weeks *             MW        week           week    number of weeks   unit1      555          1             26           7   unit2      555         27             52           5   unit3      180          1             26           2   unit4      180          1             26           1   unit5      640         27             52           5   unit6      640          1             26           3   unit7      640          1             26           3   unit8      555         27             52           6   unit9      276          1             26          10   unit10     140          1             26           4   unit11      90          1             26           1   unit12      76         27             52           3   unit13      76          1             26           2   unit14      94          1             26           4   unit15      39          1             26           2   unit16     188          1             26           2   unit17      58         27             52           1   unit18      48         27             52           2   unit19     137         27             52           1   unit20     469         27             52           4   unit21      52          1             26           3 ; table manpower(i,t) 'Manpower required for each week'         week1 week2 week3 week4 week5 week6 week7 week8 week9 week10 unit1    10    10     5     5     5     5     3 unit2    10    10    10     5     5 unit3    15    15 unit4    20 unit5    10    10    10    10    10 unit6    15    15    15 unit7    15    15    15 unit8    10    10    10     5     5     5 unit9     3     2     2     2     2     2     2     2     2     3 unit10   10    10     5     5 unit11   20 unit12   10     1     5    15 unit13   15    15 unit14   10    10    10    10 unit15   15    15 unit16   15    15 unit17   20 unit18   15    15 unit19   15 unit20   10    10    10    10 unit21   10    10    10 ;

Just to be sure I added some checks:

set error(i,t) 'check for mismatch between manpower and outage-weeks'; error(i,t)$(manpower(i,t)=0 and ord(t)<=data(i,'outage-weeks')) = yes; error(i,t)$(manpower(i,t)<>0 and ord(t)>data(i,'outage-weeks')) = yes; abort$card(error) "manpower mismatch",error;

Low and behold, we see:

----     93 manpower mismatch ----     93 SET error  check for mismatch between manpower and outage-weeks              week4 unit12         YES **** Exec Error at line 93: Execution halted: abort$1 'manpower mismatch'

Indeed we have for this unit a problem in the manpower allocation.