Strict Inequalities in Optimization Models

An often seen question is:

Can I write an inequality of the form:

\[\sum_i a_i x_i < b \]

The obvious answer is no. LP, MIP and NLP solvers only allow \(\le\) and \(\ge\) inequalities.

Here are some notes:

• Here is the mathematical answer. Strict inequalities cause the feasible region to be an open set. Mathematically, a maximum or minimum over an open set does not exist.  In your theory book you should see that optimization takes place over compact sets.
• A CS answer could be that the difference between \(<\) and \(\le\) is not that meaningful in the presence of floating point computations and their round-off errors.
• The same thing holds for bounds: e.g. we write \(x \in [0,1]\) and not \(x \in (0,1)\).
• One could do something like: replace “\(x+y<1\)” by “\(x+y \le 0.999\)”.
• Be aware that solvers apply a feasibility tolerance: variables and equations are allowed to be slightly infeasible. So \(\sum a_i x_i \le b\) really means:
  

  \[\sum_i a_i x_i \le b +\epsilon\]

  where \(\epsilon>0\) is the feasibility tolerance.
• If \(x\) and \(y\) are binary variables, note that they can assume values slightly smaller or larger than 0 or 1 (similar for integer variables). Solvers apply a so-called integer feasibility tolerance.
• That also means we should not write ”\(x+y\le 1-\varepsilon\)” with say \(\varepsilon=1.0 \times 10^{-15}\). Our tolerance should be larger than the feasibility tolerance. Even more complications can arise as the result of integer tolerances and scaling. So our tolerance should be relatively large.
• If \(x\) and \(y\) are binary (or integer) variables, we can replace “\(x+y<2\)” by “\(x+y \le 1\)”.
• I don’t really know why so many people are asking for this: I never have the urgent need to use strict inequalities in practical models. 

Piecewise Linear Functions

Here is an example of the last point. Say we want to implement a piecewise linear function as below, taken from (1):

 

\[f(x)=\begin{cases} -x-3&\text{if }x \le –3\\   x+3&\text{if }-3<x<0\\   -2x+3&\text{if }0 \le x<3\\   0.5x-4.5&\text{if }x \ge 3 \end{cases}\]

In practice we would make things ambiguous at the kinks:

\[f(x)=\begin{cases} -x-3&\text{if }x \le –3\\   x+3&\text{if }-3\le x\le 0\\   -2x+3&\text{if }0 \le x\le 3\\   0.5x-4.5&\text{if }x \ge 3 \end{cases}\]

Of course here the function \(f(x)\) is continuous and it does not make a difference. If the function \(f(x)\) would be discontinuous (i.e. jumps instead of kinks) we can let the model pick the “best” (e.g. cheapest or most profitable) segment. In almost any case this is a good choice.

Floor function

An example of a discontinuous piecewise linear function is the floor function \(\lfloor x \rfloor\). This picture is from (2):

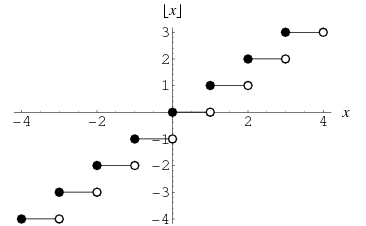
In practical model we would not care about what is precisely happening at the integer points (most likely picking the “best” value would be a good strategy: we would not want suboptimal solutions based on some artificial \(\varepsilon\) argument). But if I want to avoid such a discussion, we could model \(y=\lfloor x \rfloor\) as:

\[\boxed{\begin{align} &y \> \text{integer}\\ &y \le x\\ &y \ge x-0.999 \end{align}}\]

Note that this would create small holes in the set of allowed \(x\) values.

References

1. Piecewise linear function, https://en.wikipedia.org/wiki/Piecewise_linear_function
2. Floor function, http://mathworld.wolfram.com/FloorFunction.html
3. GAMS: Piecewise linear functions with SOS2 variables, http://yetanothermathprogrammingconsultant.blogspot.com/2009/06/gams-piecewise-linear-functions-with.html