ifthen adventures in GAMS (and R)

GAMS has a function ifthen which can be used in equations. For example:

e.. y =e= ifthen(x<1,(1+x)/2,sqrt(x));

This function implements:

\[y=\begin{cases}\displaystyle\frac{1+x}{2}&\text{if $x<1$}\\                          \sqrt{x}&\text{if $x\ge 1$}\end{cases}\]

This is a perfectly smooth function: it is continuous and differentiable.

However when we use it in GAMS we are in for a surprise:

variable x,y; equation e; e.. y =e= ifthen(x<1,(1+x)/2,sqrt(x)); x.fx = -1; model m /all/; solve m minimizing x using dnlp;

Here we fix \(x=-1\) so we just want to evaluate at that point. We see:

**** Exec Error at line 4: sqrt: FUNC DOMAIN: x < 0

The underlying reason is that GAMS always evaluates both branches. Obviously we would much prefer it would not do that.

If we replace fixing the variable by:

x.lo = -1; x.l = 2;

i.e. start at \(x=2\) and move to the optimal value \(x=-1\), we see:

C O N O P T 3   version 3.17A    Copyright (C)   ARKI Consulting and Development A/S                    Bagsvaerdvej 246 A                    DK-2880 Bagsvaerd, Denmark   Iter Phase Ninf   Infeasibility   RGmax    NSB   Step InItr MX OK      0   0        1.4142135624E+00 (Input point)                   Pre-triangular equations:   0                   Post-triangular equations:  1      1   0        0.0000000000E+00 (After pre-processing)      2   0        0.0000000000E+00 (After scaling) ** Feasible solution. Value of objective =    2.00000000000   Iter Phase Ninf     Objective     RGmax    NSB   Step InItr MX OK     11   3        6.5613264487E-03 1.0E+00     1 3.9E-03      F  F     21   3        1.6608134823E-07 1.0E+00     1 6.0E-08      F  F     31   3        3.2205059005E-13 1.0E+00     1 1.5E-11      F  T     41   3        8.5912908646E-17 1.0E+00     1 2.2E-16      F  T     51   3        5.0871607672E-23 1.0E+00     1 3.4E-21      F  T     52   3        5.0871607672E-23 1.0E+00     1 ** Feasible solution. Convergence too slow. The change in objective    has been less than 3.0000E-12 for 20 consecutive iterations

The solver gets stuck at \(x=0\). This is obviously incorrect. The only hint of the source of the problem is listed here:

RESOURCE USAGE, LIMIT          0.062      1000.000 ITERATION COUNT, LIMIT        52    2000000000 EVALUATION ERRORS            803             0

This behavior is really a bug: we should see good feedback where the problem with domain errors originates from. Note that setting the limit of allowed evaluation errors (using option domlim) does not help in this case.

R

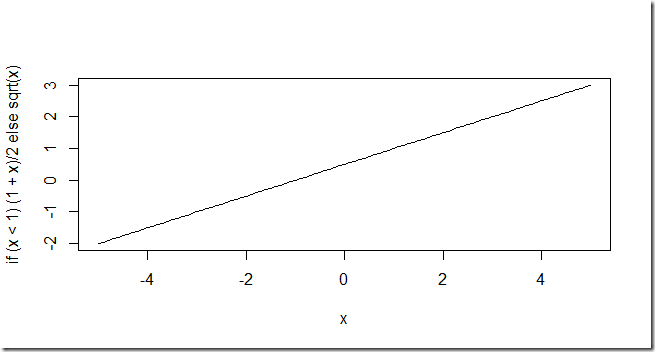
Interestingly R has something similar. Besides the standard if statement it has a vectorized ifelse function. The standard if is not vectorized which we can see from:

> curve(if (x<1) (1+x)/2 else sqrt(x),-5,5) Warning message: In if (x < 1) (1 + x)/2 else sqrt(x) :   the condition has length > 1 and only the first element will be used

This only plots \(f(x)=\displaystyle\frac{1+x}{2}\):

Basically this if statement is interpreted as:

if (x[1]<1) (1+x)/2 else sqrt(x)

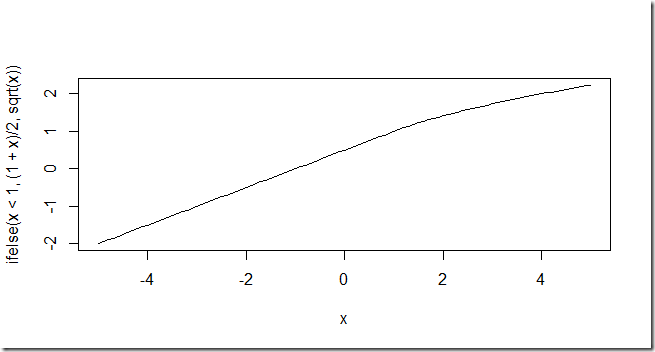
With ifelse we get better results:

> curve(ifelse(x<1,(1+x)/2,sqrt(x)),-5,5) Warning message: In sqrt(x) : NaNs produced

The plot is correct, but from the warning message we see that ifelse is also evaluating the \(\sqrt{x}\) for all \(x\). The ifelse function evaluates both branches.

To be precise this is only for vector arguments with some but not all \(x_i<1\). For scalar arguments (vectors of length one) or more general if all elements of the vector are either less than one or all are \(\ge 1\) things are ok:

Basically this is due to lazy but vector “all-or-nothing” evaluation.

Workaround

Of course the workaround is easy in this particular case. We can use something like:

e.. y =e= ifthen(x<1,(1+x)/2,sqrt(abs(x)));

Now the solver has no problems with this model, and can solve it very quickly (again with starting point \(x=2\) and optimal solution \(x=-1\)):

C O N O P T 3   version 3.17A    Copyright (C)   ARKI Consulting and Development A/S                    Bagsvaerdvej 246 A                    DK-2880 Bagsvaerd, Denmark   Iter Phase Ninf   Infeasibility   RGmax    NSB   Step InItr MX OK      0   0        1.4142135624E+00 (Input point)                   Pre-triangular equations:   0                   Post-triangular equations:  1      1   0        0.0000000000E+00 (After pre-processing)      2   0        0.0000000000E+00 (After scaling) ** Feasible solution. Value of objective =    2.00000000000   Iter Phase Ninf     Objective     RGmax    NSB   Step InItr MX OK      4   3       -1.0000000000E+00 0.0E+00     0 ** Optimal solution. There are no superbasic variables.

The same trick can be used in the R code:

curve(ifelse(x<1,(1+x)/2,sqrt(abs(x))),-5,5)

does not give any errors or warnings.