The Mixed Integer Programming formulations for solving the puzzles Sudoku and KenKen have a major trait they share: the basic data structure is a binary decision variable:
\[x_{i,j,k} = \begin{cases}1 & \text{if cell $(i,j)$ has the value $k$}\\
0 & \text{otherwise}\end{cases}\] |
Such a binary variable allows us to easily formulate so-called ‘all-different’ constructs (1). E.g. if each row \(i\) having \(n\) cells must have different values \(1..n\) in each cell, we can write:
\[\boxed{\begin{align}&\sum_j x_{i,j,k} = 1 &&\forall i, k&& \text{value $k$ appears once in row $i$}\\
&\sum_k x_{i,j,k} = 1&&\forall i, j&&\text{cell $(i,j)$ contains one value}\\
&x_{i,j,k} \in \{0,1\}
\end{align}}\] |
If we want to recover the value of a cell \((i,j)\) we can introduce a variable \(v_{i,j}\) with:
| \[v_{i,j} = \sum_k k \cdot x_{i,j,k}\] |
Detail: this is essentially what is sometimes called a set of accounting rows. We could also do this in post-processing outside the optimization model.
Below I extend this basic structure to a model that solves the Sudoku problem. Next we tackle the KenKen problem. We do this along the lines of (6) but we use a different, more straightforward logarithmic linearization technique for the multiplications and divisions.
Sudoku


On the left we have a Sudoku puzzle and on the right we see the solution (2).
In Sudoku we need uniqueness along the rows, the columns and inside the 3 x 3 sub-squares. The constraints that enforce these uniqueness conditions are:
\[\boxed{\begin{align}&\sum_j x_{i,j,k} = 1 &&\forall i, k&& \text{value $k$ appears once in row $i$}\\
&\sum_j x_{i,j,k} = 1 &&\forall j, k&& \text{value $k$ appears once in column $j$}\\
&\sum_{i,j|u_{s,i,j}} x_{i,j,k} = 1 &&\forall s, k&& \text{value $k$ appears once in square $s$}\\
&\sum_k x_{i,j,k} = 1&&\forall i, j&&\text{cell $(i,j)$ contains one value}
\end{align}}\] |
Here \(u_{s,i,j}\) contains the elements \(i,j\) for square \(s\). With this we have two issues left: How can we build up \(u_{s,i,j}\) and how can we fix the given values in the Sudoku problem.
Populate areas
We number the squares as follows:

Let’s see if we can populate \(u_{s,i,j}\) without entering data manually and without using loops. We can invent a function \(s=f(i,j)\) that takes a row and column number and returns the number of the square as follows:
| \[f(i,j) = 3\left\lceil i/3 \right\rceil + \left\lceil j/3 \right\rceil – 3\] |
Here the funny brackets indicate the ceiling function. E.g. \(f(4,7)= 3\left\lceil 4/3 \right\rceil + \left\lceil 7/3 \right\rceil –3 = 3\cdot 2+3-3=6\). This means we can populate \(u\) as in:
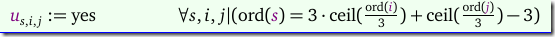
When we take a step back, we can consider rows and columns as just another particularly shaped block. So we add to our set \(u\) the individual rows and columns:

To verify we get the correct data structure, you may want to display u:
| ---- 23 SET u areas with unique values c1 c2 c3 c4 c5 c6 c7 c8 c9 r1.r1 YES YES YES YES YES YES YES YES YES
r2.r2 YES YES YES YES YES YES YES YES YES
r3.r3 YES YES YES YES YES YES YES YES YES
r4.r4 YES YES YES YES YES YES YES YES YES
r5.r5 YES YES YES YES YES YES YES YES YES
r6.r6 YES YES YES YES YES YES YES YES YES
r7.r7 YES YES YES YES YES YES YES YES YES
r8.r8 YES YES YES YES YES YES YES YES YES
r9.r9 YES YES YES YES YES YES YES YES YES
c1.r1 YES
c1.r2 YES
c1.r3 YES
c1.r4 YES
c1.r5 YES
c1.r6 YES
c1.r7 YES
c1.r8 YES
c1.r9 YES
c2.r1 YES
c2.r2 YES
c2.r3 YES
c2.r4 YES
c2.r5 YES
c2.r6 YES
c2.r7 YES
c2.r8 YES
c2.r9 YES
c3.r1 YES
c3.r2 YES
c3.r3 YES
c3.r4 YES
c3.r5 YES
c3.r6 YES
c3.r7 YES
c3.r8 YES
c3.r9 YES
c4.r1 YES
c4.r2 YES
c4.r3 YES
c4.r4 YES
c4.r5 YES
c4.r6 YES
c4.r7 YES
c4.r8 YES
c4.r9 YES
c5.r1 YES
c5.r2 YES
c5.r3 YES
c5.r4 YES
c5.r5 YES
c5.r6 YES
c5.r7 YES
c5.r8 YES
c5.r9 YES
c6.r1 YES
c6.r2 YES
c6.r3 YES
c6.r4 YES
c6.r5 YES
c6.r6 YES
c6.r7 YES
c6.r8 YES
c6.r9 YES
c7.r1 YES
c7.r2 YES
c7.r3 YES
c7.r4 YES
c7.r5 YES
c7.r6 YES
c7.r7 YES
c7.r8 YES
c7.r9 YES
c8.r1 YES
c8.r2 YES
c8.r3 YES
c8.r4 YES
c8.r5 YES
c8.r6 YES
c8.r7 YES
c8.r8 YES
c8.r9 YES
c9.r1 YES
c9.r2 YES
c9.r3 YES
c9.r4 YES
c9.r5 YES
c9.r6 YES
c9.r7 YES
c9.r8 YES
c9.r9 YES
s1.r1 YES YES YES
s1.r2 YES YES YES
s1.r3 YES YES YES
s2.r1 YES YES YES
s2.r2 YES YES YES
s2.r3 YES YES YES
s3.r1 YES YES YES
s3.r2 YES YES YES
s3.r3 YES YES YES
s4.r4 YES YES YES
s4.r5 YES YES YES
s4.r6 YES YES YES
s5.r4 YES YES YES
s5.r5 YES YES YES
s5.r6 YES YES YES
s6.r4 YES YES YES
s6.r5 YES YES YES
s6.r6 YES YES YES
s7.r7 YES YES YES
s7.r8 YES YES YES
s7.r9 YES YES YES
s8.r7 YES YES YES
s8.r8 YES YES YES
s8.r9 YES YES YES
s9.r7 YES YES YES
s9.r8 YES YES YES
s9.r9 YES YES YES |
This means we can reduce the model equations to just:
\[\boxed{\begin{align}&\sum_{i,j|u_{a,i,j}} x_{i,j,k} = 1 &&\forall a, k&& \text{value $k$ appears once in area $a$}\\
&\sum_k x_{i,j,k} = 1&&\forall i, j&&\text{cell $(i,j)$ contains one value}\\
&x_{i,j,k} \in \{0,1\}
\end{align}}\] |
Fixing initial values
If we use the variables \(v_{i,j}\) in the model, we can use them to fix the initial values.

If we don’t have the \(v\) variables in the model we can fix the underlying \(x\) variables:

Complete model

The input is most conveniently organized as a table:
| table v0(i,j)
c1 c2 c3 c4 c5 c6 c7 c8 c9
r1 5 3 7
r2 6 1 9 5
r3 9 8 6
r4 8 6 3
r5 4 8 3 1
r6 7 2 6
r7 6 2 8
r8 4 1 9 5
r9 8 7 9
;
|
The output looks like:
| ---- 49 PARAMETER v c1 c2 c3 c4 c5 c6 c7 c8 c9 r1 5 3 4 6 7 8 9 1 2
r2 6 7 2 1 9 5 3 4 8
r3 1 9 8 3 4 2 5 6 7
r4 8 5 9 7 6 1 4 2 3
r5 4 2 6 8 5 3 7 9 1
r6 7 1 3 9 2 4 8 5 6
r7 9 6 1 5 3 7 2 8 4
r8 2 8 7 4 1 9 6 3 5
r9 3 4 5 2 8 6 1 7 9 |
KenKen

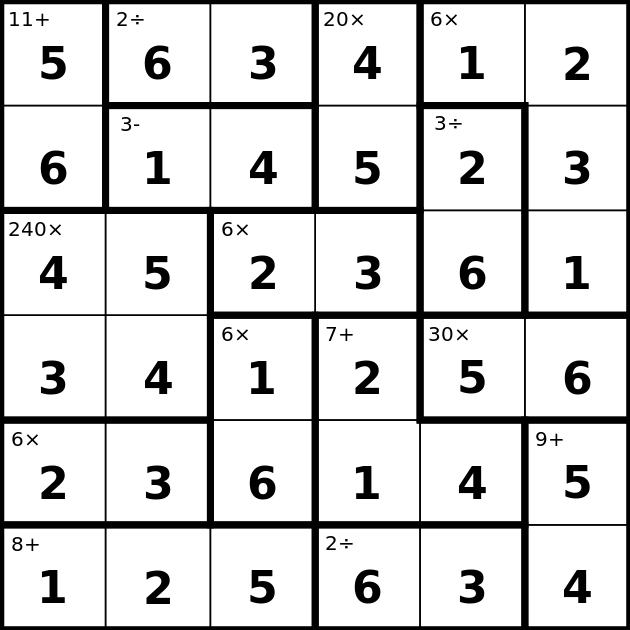
On the left we have a KenKen puzzle and on the right we see the solution (4).
In the KenKen puzzle we need to have unique values along the rows and the columns. As we have seen in Sudoku example, this is straightforward. We can formulate this as:
\[\boxed{\begin{align}&\sum_j x_{i,j,k} = 1 &&\forall i, k&& \text{value $k$ appears once in row $i$}\\
&\sum_i x_{i,j,k} = 1 &&\forall j, k&& \text{value $k$ appears once in column $j$}\\
&\sum_k x_{i,j,k} = 1&&\forall i, j&&\text{cell $(i,j)$ contains one value}\\
&x_{i,j,k} \in \{0,1\}
\end{align}}\] |
As in the Sudoku example, we can combine the first two constraints into a single one:
| \[\sum_{i,j|u_{s,i,j}} x_{i,j,k} = 1 \>\>\forall s,k\] |
Lemma
In the subsequent discussion we will make use of the following logarithmic transformation:
Given the construct
| \[v_{i,j} = \sum_k k \cdot x_{i,j,k}\] |
where \(x_{i,j,k}\in \{0,1\}\), \(k=1,\dots,K\) and \(\displaystyle\sum_k x_{i,j,k}=1\) we have
| \[\log(v_{i,j}) = \sum_k \log(k) \cdot x_{i,j,k}\] |
In addition to these uniqueness constraints we have a slew of restrictions related to collections of cells - these are called the cages. Each cage has a rule and a given answer. For instance the first cage in the example above with rule 11+ means that the values of the cells in the cage need to add up to 11 (the solution turns out to be 5+6). Let’s discuss them in detail:
- n this is a single cell with a given value. This case is not present in the data set in our example above. The rule is easy: just put the number in the cell \((i,j)\): \(v_{i,j} = n\),

For this example we would fix this cell to the value 1. - n+ indicates we add up the values in the cage and the result should be n. This is a simple linear constraint: \[\sum_{i,j|C{i,j}} v_{i,j} = n\]
- n- is a cage with just two cells where the absolute value difference between the values of the two cells is n. I.e. \[|v_{i_1,j_1}- v_{i_2,j_2}|=n\] In (6) it is proposed to model this in a linear fashion with the help of an additional binary variable as: \[v_{i_1,j_1}- v_{i_2,j_2}=n(2 \delta-1)\] where \(\delta \in \{0,1\}\).
- n* indicates we multiply all values in the cage: \[\prod_{i,j|C{i,j}} v_{i,j} = n\] In (6) a number of possible linearizations are mentioned, some of them rather complicated with such things as prime number factorizations. Let me suggest a much simpler approach using logarithms. We have: \[\begin{align}&\prod_{i,j|C{i,j}} v_{i,j} = n\\ \Longrightarrow\>\> & \sum_{i,j|C_{i,j}} \log(v_{i,j}) = \log(n)\\ \Longrightarrow\>\> & \sum_{i,j|C_{i,j}} \sum_k \log(k) x_{i,j,k} = \log(n)\end{align}\] The last constraint is linear in the decision variables \(x_{i,j,k}\)!. We have used here that \(\log(v_{i,j})=\sum_k \log(k) x_{i,j,k}\). This simpler linearization is not mentioned in (6).
Note that we can always evaluate \(\log(k)\) and \(\log(n)\) as \(k\ge 1\) and \(n \ge 1\). - n÷ this operation has two cells, and indicates division and can be described more formally: \[\frac{v_{i_1,j_1}}{v_{i_2,j_2}}=n \>\text{or}\>\frac{v_{i_2,j_2}}{v_{i_1,j_1}}=n\] In (6) the following linearization is proposed:\[\begin{align} &v_{i_1,j_1}-n\cdot v_{i_2,j_2} \ge 0-M\cdot \delta\\&v_{i_1,j_1}-n\cdot v_{i_2,j_2} \le 0+M\cdot \delta\\&v_{i_2,j_2}-n\cdot v_{i_1,j_1} \ge 0-M\cdot (1-\delta)\\&v_{i_2,j_2}-n\cdot v_{i_1,j_1} \le 0+M\cdot (1-\delta)\\&\delta\in\{0,1\}\end{align}\] Again I would suggest a simpler linearization: \[\begin{align}&\frac{v_{i_1,j_1}}{v_{i_2,j_2}}=n \>\text{or}\>\frac{v_{i_2,j_2}}{v_{i_1,j_1}}=n\\ \Longrightarrow\>\>&\log(v_{i_1,j_1})-\log(v_{i_2,j_2})=\log(n) \> \text{or} \>\log(v_{i_2,j_2})-\log(v_{i_1,j_1})=\log(n)\\ \Longrightarrow\>\>&|\log(v_{i_1,j_1})-\log(v_{i_2,j_2})|=\log(n)\\ \Longrightarrow\>\>&\log(v_{i_1,j_1})-\log(v_{i_2,j_2})=\log(n)(2\delta-1)\\ \Longrightarrow\>\>&\sum_k \log(k) x_{i_1,j_1,k}-\sum_k \log(k) x_{i_2,j_2,k}=\log(n)(2\delta-1)\end{align}\]
I believe we can assume \(n\ge 1\) even for subtraction, hence we can safely apply the logarithm.
Complete Model
We have now all the pieces to assemble the complete model.

The sets are almost identical to the Sudoku model. We have introduced new sets \(op\), \(p\) and \(c\). The unique values will be handled through a set \(u\) as before, only now this set is simpler: only rows and columns (no squares).
We have a somewhat complicated parameter that holds the problem data:

The data can be entered as follows:
parameter operation(c,op,i,j) /
cage1 .plus.(r1,r2).c1 11
cage2 .div .r1.(c2,c3) 2
cage3 .min .r2.(c2,c3) 3
cage4 .mul .(r1,r2).c4 20
cage5 .mul .(r1.c5, (r1,r2,r3).c6) 6
cage6 .div .(r2,r3).c5 3
cage7 .mul .(r3,r4).(c1,c2) 240
cage8 .mul .r3.(c3,c4) 6
cage9 .mul .(r4,r5).c3 6
cage10.plus.((r4,r5).c4, r5.c5) 7
cage11.mul .r4.(c5,c6) 30
cage12.mul .r5.(c1,c2) 6
cage13.plus.(r5,r6).c6 9
cage14.plus.r6.(c1*c3) 8
cage15.div .r6.(c4,c5) 2
/; |
We need to extract data from this data structure to make things easier:

The sets \(cells\), \(cellp\) and the parameter \(n\) look like:
| ---- 53 SET cells cells in cage c1 c2 c3 c4 c5 c6 cage1 .r1 YES
cage1 .r2 YES
cage2 .r1 YES YES
cage3 .r2 YES YES
cage4 .r1 YES
cage4 .r2 YES
cage5 .r1 YES YES
cage5 .r2 YES
cage5 .r3 YES
cage6 .r2 YES
cage6 .r3 YES
cage7 .r3 YES YES
cage7 .r4 YES YES
cage8 .r3 YES YES
cage9 .r4 YES
cage9 .r5 YES
cage10.r4 YES
cage10.r5 YES YES
cage11.r4 YES YES
cage12.r5 YES YES
cage13.r5 YES
cage13.r6 YES
cage14.r6 YES YES YES
cage15.r6 YES YES
---- 53 SET cellp ordered cell numbers
cage1 .p1.r1.c1
cage1 .p2.r2.c1
cage2 .p1.r1.c2
cage2 .p2.r1.c3
cage3 .p1.r2.c2
cage3 .p2.r2.c3
cage4 .p1.r1.c4
cage4 .p2.r2.c4
cage5 .p1.r1.c5
cage5 .p2.r1.c6
cage5 .p3.r2.c6
cage5 .p4.r3.c6
cage6 .p1.r2.c5
cage6 .p2.r3.c5
cage7 .p1.r3.c1
cage7 .p2.r3.c2
cage7 .p3.r4.c1
cage7 .p4.r4.c2
cage8 .p1.r3.c3
cage8 .p2.r3.c4
cage9 .p1.r4.c3
cage9 .p2.r5.c3
cage10.p1.r4.c4
cage10.p2.r5.c4
cage10.p3.r5.c5
cage11.p1.r4.c5
cage11.p2.r4.c6
cage12.p1.r5.c1
cage12.p2.r5.c2
cage13.p1.r5.c6
cage13.p2.r6.c6
cage14.p1.r6.c1
cage14.p2.r6.c2
cage14.p3.r6.c3
cage15.p1.r6.c4
cage15.p2.r6.c5
---- 53 PARAMETER n value for each cage
cage1 11.000, cage2 2.000, cage3 3.000, cage4 20.000, cage5 6.000, cage6 3.000
cage7 240.000, cage8 6.000, cage9 6.000, cage10 7.000, cage11 30.000, cage12 6.000
cage13 9.000, cage14 8.000, cage15 2.000 |
The variables in the model are as follows:

The loop to fix some cells is not used in this data set as we don’t have fixed values in the data. The rest of the model looks like:

The summations in the subtraction and divisions are a little bit misleading. These just pick the value of the first (p1) and second (p2) cell in the cage c. In the division equation we pick up the logarithm of the value. Here are the actually generated MIP rows:
| ---- subtraction =E= cages with subtraction subtraction(cage3).. v(r2,c2) - v(r2,c3) + 6*delta(cage3) =E= 3 ; (LHS = 0, INFES = 3 ****)
---- division =E= cages with division division(cage2).. logv(r1,c2) - logv(r1,c3) + 1.38629436111989*delta(cage2) =E= 0.693147180559945 ;
(LHS = 0, INFES = 0.693147180559945 ****)
division(cage6).. logv(r2,c5) - logv(r3,c5) + 2.19722457733622*delta(cage6) =E= 1.09861228866811 ;
(LHS = 0, INFES = 1.09861228866811 ****)
division(cage15).. logv(r6,c4) - logv(r6,c5) + 1.38629436111989*delta(cage15) =E= 0.693147180559945 ;
(LHS = 0, INFES = 0.693147180559945 ****) |
In equations \(calclogv\) we could restrict the calculation of \(logv\) only for those cells \((i,j)\) where we have a multiplication or division. Similarly, we can calculate \(v_{i,j}\) only for cells where we do addition or subtraction. Now we calculate too many \(logv\)’s and \(v\)'s. For this small case this is not an issue. Furthermore a good LP/MIP presolver will probably detect a variable that is not used anywhere else, and will remove the variable and the accompanying equation.
The final result looks like:
| ---- 101 VARIABLE v.L value c1 c2 c3 c4 c5 c6 r1 5.000 6.000 3.000 4.000 1.000 2.000
r2 6.000 1.000 4.000 5.000 2.000 3.000
r3 4.000 5.000 2.000 3.000 6.000 1.000
r4 3.000 4.000 1.000 2.000 5.000 6.000
r5 2.000 3.000 6.000 1.000 4.000 5.000
r6 1.000 2.000 5.000 6.000 3.000 4.000
|
Conclusion
To solve the KenKen puzzle as a Mixed Integer Program, we can start with a data structure similar as used in the Sodoku formulation: \(x_{i,j,k}\in\{0,1\}\). Using different linearizations from the ones shown in (6) we can solve then KenKen problem easily with a MIP solver.
References
- All-different and Mixed Integer Programming, http://yetanothermathprogrammingconsultant.blogspot.com/2016/05/all-different-and-mixed-integer.html
- Sudoku, https://en.wikipedia.org/wiki/Sudoku
- Sudoku Puzzle, http://www.nytimes.com/crosswords/game/sudoku/hard
- KenKen, https://en.wikipedia.org/wiki/KenKen
- KenKen Puzzle, http://www.nytimes.com/ref/crosswords/kenken.html
- Vardges Melkonian, “An Integer Programming Model for the KenKen Problem”, American Journal of Operations Research, 2016, 6, 213-225. [link] Contains a complete AMPL model.
- Andrew C. Bartlett, Timothy P. Chartier, Amy N. Langville, Timothy D. Rankin, “An Integer Programming Model for the Sudoku Problem”, The Journal of Online Mathematics and Its Applications, Vol.8, 2008, [link]