Typically income data is presented in income classes:
| Income Class | Number of Observations |
| 0-$20000 | 1036 |
| $20000-$40000 | 495 |
| $40000-$60000 | 201 |
| $60000-$80000 | 102 |
| $80000+ | 38 |
In order to find the mean income based on such data we can fit e.g. a Pareto Distribution. One way of doing this is with a max likelihood estimation procedure. From http://www.math.uconn.edu/~valdez/math3632s10/M3632Week10-S2010.pdf we have:
This is easy to code in GAMS, using a Pareto distribution:
| |
We use here that F(0) = 0 and F(INF) = 1 for the CDF of the Pareto distribution.
Note this approach can be also used to estimate the number of millionaires (ie income > 1e6) even though this number is hidden in the last income class.
Looking at http://www.jstor.org/stable/1914015 I was a little bit confused by
however I think we can arrive at the earlier likelihood function. The factor n! can be dropped as it is constant. Taking logs we see:
The last sum can be dropped as it is also constant. (Of course this can also be deducted directly from the product in EQ2).

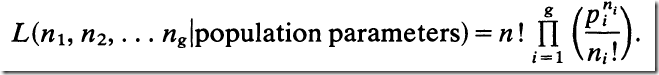

No comments:
Post a Comment