Implied Multiple Objectives

In [1] a simple problem was posed:

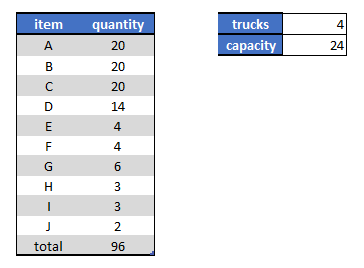
Given data:

try to load the trucks such that they have as few different items as possible. It is noted that our total truck capacity is exactly equal to the total quantity.

This looks like a simple, well-stated problem. We can minimize the maximum of the count of different items, or the sum. Here are a few solutions to illustrate this:

If we minimize the max count we can find the first or second solution: both have an optimal max count of 3. If we only focus on the sum, we can find the first or the last solution, both with a sum count of 11. The conclusion is: if we use min max count or min sum count as objective, we may see undesirable outcomes. So, if we want to develop a model that has a preference for solutions like the first one, we actually have to look at both, and use a multiple objective problem:

1. Minimize the max count
2. Minimize the sum count

(It is noted that here we have a case where there is a solution with optimal max count and optimal sum count. Often this is not the case: there may be trade-offs between the different objectives.)

A model using this approach can look like:

Weighted sum multi-objective model

\[\begin{align} \min \> & \color{DarkRed}{\mathit{MaxCount}} + \color{DarkBlue} w\cdot \color{DarkRed}{\mathit{SumCount}}\\ & \sum_j \color{DarkRed} x_{i,j} = \color{DarkBlue}{\mathit{Quantity}_i} & \forall i \\ & \sum_i \color{DarkRed} x_{i,j} \le \color{DarkBlue}{\mathit{Capacity}} & \forall j \\ & \color{DarkRed} x_{i,j} \le \min(\color{DarkBlue}{\mathit{Quantity}_i},\color{DarkBlue}{\mathit{Capacity}}) \cdot \color{DarkRed} y_{i,j} & \forall i,j \\ & \color{DarkRed}{\mathit{MaxCount}} \ge \sum_i \color{DarkRed} y_{i,j} & \forall j \\ & \color{DarkRed}{\mathit{SumCount}} = \sum_{i,j} \color{DarkRed} y_{i,j} \\ & \color{DarkRed} x_{i,j} \ge 0 \\ & \color{DarkRed} y_{i,j} \in \{0,1\} \end{align}\]

The scalar \(w>0\) indicates the trade-off between MaxCount and SumCount.

Special Case

If we want to first optimize for MaxCount and then for SumCount, we can choose a small value for \(w\), e.g. \(w=0.01\). An alternative approach for this case would be:

1. Solve with objective: \(\min \mathit{MaxCount}\)
2. Fix MaxCount to its optimal value
3. Solve with objective: \(\min \mathit{SumCount}\)

Quadratic Objective

Interestingly, there is a single objective that is an alternative for our multi-objective model:

Quadratic model

\[\begin{align} \min \> & \sum_j \left( \sum_i \color{DarkRed} y_{i,j} \right)^2 \\ & \sum_j \color{DarkRed} x_{i,j} = \color{DarkBlue}{\mathit{Quantity}_i} & \forall i \\ & \sum_i \color{DarkRed} x_{i,j} \le \color{DarkBlue}{\mathit{Capacity}} & \forall j \\ & \color{DarkRed} x_{i,j} \le \min(\color{DarkBlue}{\mathit{Quantity}_i},\color{DarkBlue}{\mathit{Capacity}}) \cdot \color{DarkRed} y_{i,j} & \forall i,j \\ & \color{DarkRed} x_{i,j} \ge 0 \\ & \color{DarkRed} y_{i,j} \in \{0,1\} \end{align}\]

This objective will automatically put more emphasis on the larger column count values \( \sum_i y_{i,j} \) but still considers the small values. In essence, this is in-between a min max count and min sum count objective. In the picture with the solutions, you can see this objective denoted by sumsq count. This objective can properly distinguish between solution 1 and the other ones.

MIQP models are often more difficult to solve than linear MIP models. For large models, we often prefer the linear formulations.

Conclusion

Even what looks like a simple problem statement can have some wrinkles. It is not unusual that a problem ends up with a model with multiple objectives. This can guide the model to better behaved solutions essentially by using more complex incentives. 

References

1. Smart grouping of item, item quantity, https://stackoverflow.com/questions/53990308/smart-grouping-of-item-item-quantity