In this post another tennis-scheduling problem is posted. In this case we deal with 20 players doing doubles in 5 rounds. That means teams of 2 players, 4 players per game, and 5 games per round.
Restriction 1
The first restriction is that a player \(i\) and player \(j\) can be team-members only once. I.e. they can play together zero or one time. There is no restriction on how many times player \(i\) can meet player \(j\) as opponent.
Restriction 2
Each player has a rating or level between 1 and 5. The level of a team is the sum of the ratings of the two players. We don’t want the level of two opposing teams to differ by more than 1.5.
The Model
The main variable is \(x_{i,r,g,t}\) which indicates if player \(i\) is playing in round \(r\), game \(g\) in team \(t\).
The level difference restriction:\[\max_{i<j} \sum_{r,g,t} x_{i,r,g,t} x_{j,r,g,t} \le 1\] is not completely trivial to linearize. The idea is to linearize the inner product by introducing additional variables \(cnt_{i,j,r,g,t}\). Then we just sum these. Note that \(cnt_{i,j,r,g,t}\) can be considered a binary variable. I relaxed that here to a positive continuous variable (you may verify this is allowed here).
The difference in level of two opposing teams is implemented using a standard variable splitting technique. We used random player levels.
The final solution is:
It is noted that instead of a bound on the level difference, we also could minimize this quantity (allowing for even better matchups where possible).
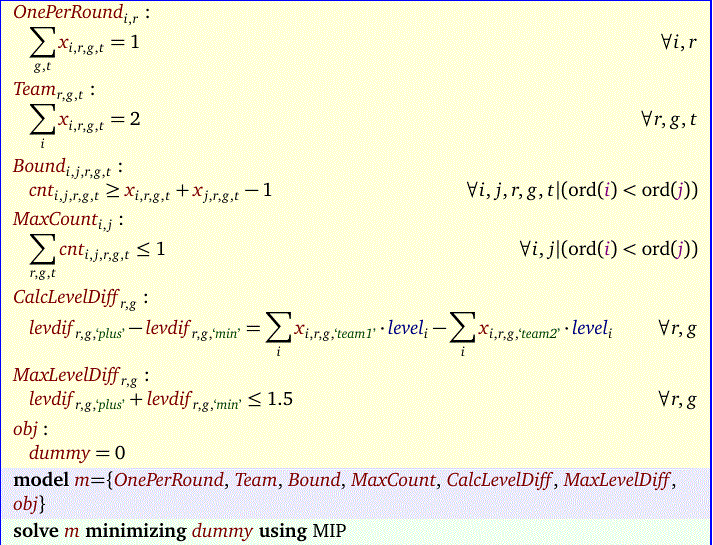
No comments:
Post a Comment