A well-known example data set for Generator Maintenance Scheduling (GMS) is the basis for quite a few computational studies using meta-heuristics. The data sets has 21 units, has time-periods of a week and asks for a yearly schedule. This note is actually a follow up to http://yetanothermathprogrammingconsultant.blogspot.com/2013/02/meta-heuristics-or-math-programming.html. To my knowledge the data sets used in the references were not solved to optimality before. So it is time to see if we can do something about that. There are a few good linear approximations that can be used to create good schedules, but here we will use the identical quadratic objective used in the other studies. This means we are dealing with an MIQP (Mixed Integer Quadratic Programming) model. Solvers like Cplex and Gurobi offer MIQP capabilities, although in general MIQPs are more difficult to solve than comparable MIP problems.
From the thesis “Decision Support for Generator Maintenance Scheduling in the Energy Sector”, Evert Barend Schlünz, Stellenbosch University, Dec 2011:
Actually, using a careful implementation of the MIQP formulation I was able to prove global optimality, with an objective of:
---- 220 PARAMETER TotalSumSquares = 1.361890E+7
This was with Gurobi on a laptop using 4 threads in 47 minutes (most of the time was spent in proving optimality – in practice we could have stopped much earlier).
Indeed the meta-heuristics are a little bit off:
Some heuristics claim better results than I have been able to verify:
But that turns out to be an infeasible solution:
Others are not as good:
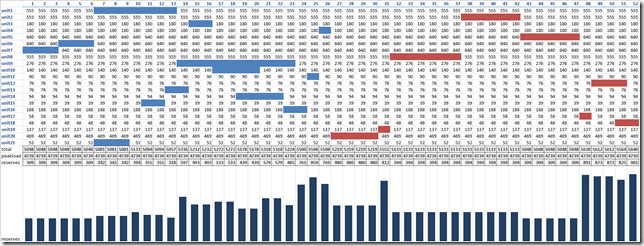
My solution is shown below:






No comments:
Post a Comment