This is a modeling construct I see re-occurring at regular intervals. One formulation is given here:
http://www.princeton.edu/~rvdb/542/lectures/lec9.pdf
I would typically write this slightly differently:
- declare t as a positive variable (this is implied by equations lower_bound and upper_bound; I prefer this to be explicit)
- add extra variable and constraint to prevent the duplicate expression (this will add rows and columns to the model but reduces the number of nonzero elements)
Another formulation I often propose is using variable splitting:
One of the pair d(i,plus),d(i,minus) will be zero. Two arguments:
- If both nonzero then not optimal: we can decrease the objective
- For Simplex methods: the basis matrix will becomes singular (not invertible) when both are in the basis. I.e. one of the pair will be non-basic, and thus zero.
Currently I am working on an application where we want to have a different weight for positive and negative deviations. This can directly be applied to the last formulation.
To back this up I generated a ridiculously large problem (although I have seen models of this size in practice!): 10000 observations and 100 independent variables. This leads to:
I ran with default settings for the solvers.
Some conclusions:
- Interior point codes do very well on some large instances
- Our improvements help (only really matters for these crazy large instances)
- Variable splitting is actually pretty good on this particular problem
- Speed improvements are similar for different solution methods (simplex, barrier)
- I also ran the problems with Gurobi’s barrier solver: almost as fast as Mosek
Update: I should have added that I have not looked at dual formulations as my main interest was a more complex model than a pure L1 regression model. We want to keep the formulation close to the problem and an explicit dual formulation makes the model much more difficult to understand and maintain.

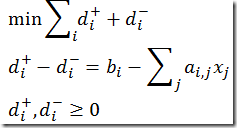

If the number variables is much smaller than the number of observations the it is normally better to solve the dual. Many optimizers including MOSEK usually figures this out automatically for you. Therefore, the best formulation is likely to depend on what dualize best.
ReplyDelete