Here is an example how to do probit estimation with GAMS. We use the dataset Table F21.1 from Greene. We estimate by forming a likelihood function which we can maximize using a standard NLP solver. First we do OLS to get a good starting point for the NLP. The OLS estimation is done through the specialized LS solver.
The reason to use a specialized least squares solver is twofold: (1) it is not easy to do least squares reliably using standard (linear) optimization tools. The normal equations allow for using an LP but in forming the normal equations you may create numerical difficulties. Of course one could solve a QP. (2) Some of the statistics useful in reporting OLS results are not trivial to compute in GAMS. A specialized solver can solve LS problems quickly and reliably with linear technology and in additional produce all kind of statistics useful in assessing the quality of the fit.
The max likelihood estimation problem is to maximize:
Here y is the dependent (binary) variable, and x are the independent variables (note: the variables are data in the optimization problem). β is the vector of coefficients to estimate (these are the decision variables in the optimization problem). Φ is the CDF of the standard normal distribution. This expression is reformulated into:
$ontext
Probit Estimation
We use OLS to get a good starting point
Erwin Kalvelagen, Amsterdam Optimization, 2009
Data:
http://pages.stern.nyu.edu/~wgreene/Text/tables/TableF21-1.txt
$offtext
set i /1*32/;
table data(i,*)
GPA TUCE PSI GRADE
1 2.66 20 0 0
2 2.89 22 0 0
3 3.28 24 0 0
4 2.92 12 0 0
5 4.00 21 0 1
6 2.86 17 0 0
7 2.76 17 0 0
8 2.87 21 0 0
9 3.03 25 0 0
10 3.92 29 0 1
11 2.63 20 0 0
12 3.32 23 0 0
13 3.57 23 0 0
14 3.26 25 0 1
15 3.53 26 0 0
16 2.74 19 0 0
17 2.75 25 0 0
18 2.83 19 0 0
19 3.12 23 1 0
20 3.16 25 1 1
21 2.06 22 1 0
22 3.62 28 1 1
23 2.89 14 1 0
24 3.51 26 1 0
25 3.54 24 1 1
26 2.83 27 1 1
27 3.39 17 1 1
28 2.67 24 1 0
29 3.65 21 1 1
30 4.00 23 1 1
31 3.10 21 1 0
32 2.39 19 1 1
;
set k 'independent variables' /constant,gpa,tuce,psi/;
parameters
y(i) 'grade'
x(k,i) 'independent variables'
;
y(i) = data(i,'grade');
x('constant',i) = 1;
x(k,i)$(not sameas(k,'constant')) = data(i,k);
parameter estimate(k,*);
*-----------------------------------------------------------
* O L S
*-----------------------------------------------------------
variable sse,coeff(k);
equation obj,fit(i);
obj.. sse =n= 0;
fit(i).. y(i) =e= sum(k, coeff(k)*x(k,i));
model ols /obj,fit/;
option lp=ls;
solve ols using lp minimizing sse;
estimate(k,'OLS') = coeff.l(k);
*-----------------------------------------------------------
* P R O B I T
*-----------------------------------------------------------
variable logl;
equation like;
like.. logl =e= sum(i$(y(i)=1), log(errorf(sum(k,coeff(k)*x(k,i)))))
+sum(i$(y(i)=0), log(1-errorf(sum(k,coeff(k)*x(k,i)))));
model mle /like/;
solve mle using nlp maximizing logl;
estimate(k,'Probit') = coeff.l(k);
display estimate;
The results are identical to the numbers published in Greene.
---- 99 PARAMETER estimate
OLS Probit
GPA 0.464 1.626
TUCE 0.010 0.052
PSI 0.379 1.426
constant -1.498 -7.452
This model looks much simpler than what is discussed here.
Updated the LS solver docs to include this example.
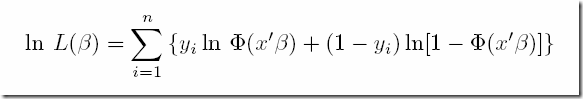

No comments:
Post a Comment