Sparse data in MSF OML

The modeling language of the Microsoft Solver Foundation does not support sparse data. I.e. if you have a parameter a[i,j] you need to have values for all a[i,j]’s and you cannot skip the zero’s. In some cases this is a little bit of problem. Adding all zero records may be a lot of work and may take a large amount of space in your spreadsheet. Sometimes it is possible to work around this problem by adding extra sets and columns. Probably the easiest way to explain this is with a small example. A network optimization problem is a good example where a sparse data structure can help. In this case we have a max flow model with a small but sparse network. In GAMS we can write:

$ontext
 
   max flow network example
 
   Data from example in
     Mitsuo Gen, Runwei Cheng, Lin Lin
     Network Models and Optimization: Multiobjective Genetic Algorithm Approach
     Springer, 2008
 
   Erwin Kalvelagen, Amsterdam Optimization, May 2008
 
$offtext
 
 
sets
   i 'nodes' /node1*node11/
   source(i)   /node1/
   sink(i)    /node11/
;
 
alias(i,j);
 
parameter capacity(i,j) /
   node1.node2   60
   node1.node3   60
   node1.node4   60
   node2.node3   30
   node2.node5   40
   node2.node6   30
   node3.node4   30
   node3.node6   50
   node3.node7   30
   node4.node7   40
   node5.node8   60
   node6.node5   20
   node6.node8   30
   node6.node9   40
   node6.node10  30
   node7.node6   20
   node7.node10  40
   node8.node9   30
   node8.node11  60
   node9.node10  30
   node9.node11  50
   node10.node11 50
/;
 
 
 
set arcs(i,j);
arcs(i,j)$capacity(i,j) = yes;
display arcs;
 
parameter rhs(i);
rhs(source) = -1;
rhs(sink) = 1;
 
variables
   x(i,j) 'flow along arcs'
   f      'total flow'
;
 
positive variables x;
x.up(i,j) = capacity(i,j);
 
equations
   flowbal(i)  'flow balance'
;
 
flowbal(i)..   sum(arcs(j,i), x(j,i)) - sum(arcs(i,j), x(i,j)) =e= f*rhs(i);
 
model m/flowbal/;
 
solve m maximizing f using lp;

The parameter capacity defines the network: where there is no capacity, we assume there no arc. We can calculate two-dimensional set arcs(i,j) to indicate which arcs exist. This can be used to simplify the flow-balance equations. Note that in GAMS only the variables that appear in the equations are actually part of the model. I.e. although we declare x(i,j), in the equations we only have x(arcs). This means we only have 22 variables x(i,j).

In OML we cannot use a sparse table for the capacities: we would need a complete table with 11x11=121 records. That would also mean that we have 121 variables. The trick is to have an explicit set arcs in the data table. As OML does not have 2-dimensional sets, I used parameters From[.], To[.] to describe the network. The complete data is below:

 
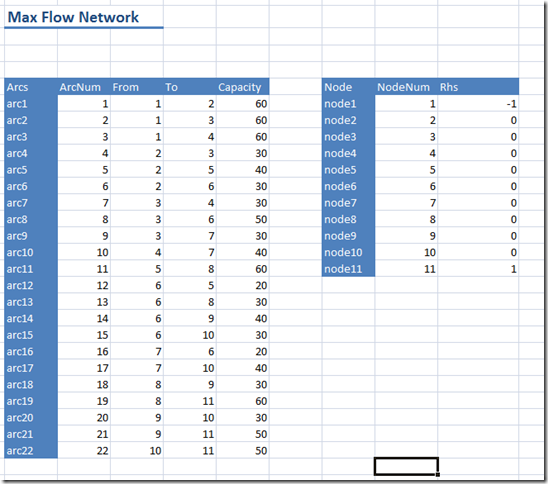
The OML model can now look like:


 
The node balance equation becomes a little bit unwieldy and less readable with this approach. This is a small, artificial example but note that quite a few models have some network component. It illustrates that leaving out sparse data handling and multidimensional sets to simplify a modeling language, although not a show stopper, comes with a cost in the form of additional complexity for the modeler. Note that in this model we still have a possibly large node table to maintain (the GAMS model handles this sparse).