In this post I displayed a CSP model for Microsoft Solver Foundation that solves the Tiling Squares problem. It was observed that a symmetry breaking constraint was really helpful. Basically it forced similar squares to be number in the x-axis direction. Of course a small extension would be to say: if same squares have the same x-coordinate, number them in the y direction. The symmetry breaking constraints can look like:
// this is to reduce some symmetry
Foreach[{i,T},{j,i+1,T},Implies[b[i]&b[j]&(Side[i]==Side[j]),x[j]>=x[i]]],
Foreach[{i,T},{j,i+1,T},Implies[
b[i]&b[j]&(Side[i]==Side[j])&(x[j]==x[i]),
y[j]>=y[i]]]
This reduces the calculation time further:
A bigger improvement can be achieved by observing that we can force lower numbered squares to be added first.
E.g. squares 9,10 and 11 have size 4. If we turn on square 10 we want to require that square 9 is also used. This can be implemented with the constraint:
FilteredForeach[{i,1,T},Side[i]==Side[i-1],Implies[b[i],b[i-1]]]
This has much effect on the computation time:
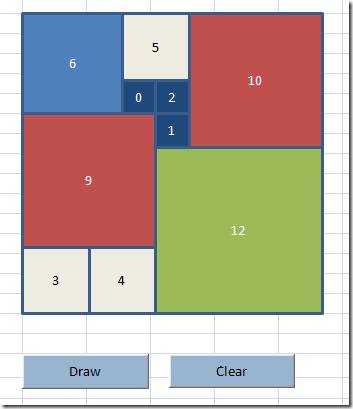
If we add numbers to the squares we see how the numbering follows these rules:
The reference sequence A036444 shows a(19)=2. I.e. we can use just a set with a maximum of two identical tiles to cover an area of (19 × 19). Indeed we can verify this with this model. The data and results are:
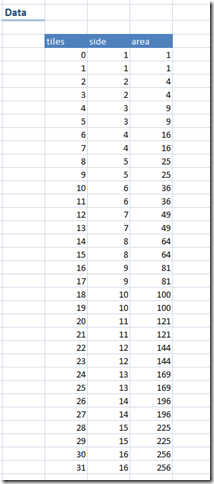 |  |



No comments:
Post a Comment