Ranking using numpy.argsort

I needed to find a ranking of a large data set. Using Python, it makes sense to look at the numpy library for this. 

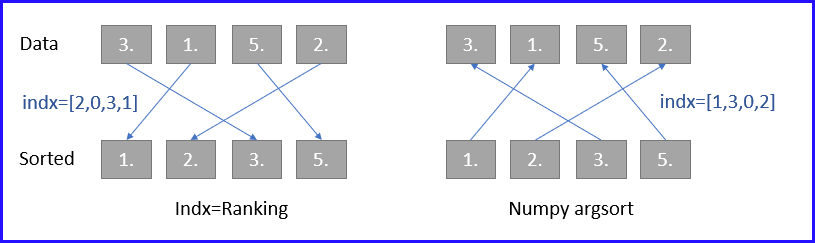
Numpy has the function argsort, which returns index positions [1]. One would think these are exactly the ranks we are after. Unfortunately, this is not the case.

>>> import numpy as np
>>> a = [3.0, 1.0, 5.0, 2.0]
>>> indx = np.argsort(a)
>>> indx
array([1, 3, 0, 2], dtype=int64)

I would expect:

 

     indx = [2, 0, 3, 1]

Actually, the reported indices are for a reversed mapping: from the (unknown) sorted vector to the original unsorted vector.

On the left is what I was after, and on the right is what argsort returns.

It is not very difficult to get the inverse mapping. Here are a few ways to do this:

1. Using loops. Use the simple fact that for an index \(p\) and its inverse mapping \(p'\), we have: \[p_i=j \iff p'_j=i\]

   >>> rank = np.empty_like(indx)
   >>> for i,j in enumerate(indx):
   ...     rank[j]=i
   ...
   >>> rank
   array([2, 0, 3, 1], dtype=int64)
   

   Looping is in general quite slow in Python. So we may want to look into some alternatives.
2. Fancy indexing[2]. Here we use the array indx to permute the values [0,1,2,3].

   >>> rank = np.empty_like(indx)
   >>> rank[indx] = np.arange(len(indx))
   >>> rank
   array([2, 0, 3, 1], dtype=int64)
   

3. Applying argsort twice[2]. This is a bit of a surprise, but it does exactly what we want.

   >>> rank=np.argsort(indx)
   >>> rank
   array([2, 0, 3, 1], dtype=int64)
   

   This one is the most intriguing of course: argsort(argsort(a)) gives the ranking.

An alternative is to use scipy.stats.rankdata. The above ranking can be replicated with:

>>> import scipy.stats as stats
>>> rank = stats.rankdata(a,method='ordinal')-1
>>> rank
array([2, 0, 3, 1], dtype=int64)

  

References

1. Numpy.argsort, https://numpy.org/doc/stable/reference/generated/numpy.argsort.html
2. Rank Values in Numpy Array, https://www.delftstack.com/howto/numpy/python-numpy-rank/