Problem
We have \(N\) jobs to schedule. Each job has a given processing time. In addition we have a setup time for the machine in between jobs. The twist is that the required setup time depends on how two consecutive jobs differ. If two jobs in a row are very similar, the intermediate setup time is small, while if they are very different, the setup time increases. An example of such a problem is running some kind of printing jobs. Changing from a black job to a white job requires extensive cleaning, while white followed by black does not require much cleaning at all. See e.g. [1].
Some extra things to think about:
- The last job performed (called initial below) may be important, as we may need to do a setup from the initial state to whatever the selected first job is.
- The setup times are organized as an \((N+1) \times N\) matrix (one extra row for the initial job).
- We can have due dates and release dates on the jobs. We need to finish a job before the due date and cannot start a job before its release date.
- We may have some precedence relations: some jobs must be finished before another.
- We want to sequence the jobs such that the completion time of the last job is minimized (of course subject to due date, release date and precedence constraints).
Example data
Some random data can help to understand the problem a bit better.
---- 26 PARAMETER proctime processing time job1 2.546, job2 8.589, job3 5.953, job4 3.710, job5 3.630, job6 3.016, job7 4.148 job8 8.706, job9 1.604, job10 5.502, job11 9.983, job12 6.209, job13 9.920, job14 7.860 job15 2.176 ---- 26 PARAMETER setup setup time job1 job2 job3 job4 job5 job6 job7 job8 job9 initial 3.559 1.638 2.000 3.676 2.741 2.439 2.406 1.526 1.600 job1 3.010 1.641 4.490 2.060 2.143 3.376 3.891 3.513 job2 1.728 3.243 4.080 2.191 3.644 4.023 3.510 2.135 job3 1.291 1.703 4.001 1.712 1.137 3.341 3.485 2.557 job4 4.134 2.200 1.502 1.277 1.808 1.020 2.078 2.999 job5 4.974 2.480 2.492 4.088 4.652 1.478 3.942 1.222 job6 1.903 2.584 2.104 1.609 4.745 1.539 2.544 2.499 job7 1.407 2.536 2.296 1.769 1.449 3.386 1.180 4.132 job8 3.026 1.637 3.628 3.096 1.498 4.947 1.912 4.107 job9 3.940 1.342 1.601 2.737 1.748 3.771 4.052 1.619 job10 1.348 3.162 1.507 3.936 1.453 2.953 4.182 2.968 3.134 job11 1.099 1.711 1.245 1.067 4.343 3.407 1.108 1.784 4.803 job12 2.573 4.222 3.164 2.563 3.231 4.731 2.395 1.033 4.795 job13 3.321 1.666 3.573 2.377 4.649 4.600 1.065 2.475 3.658 job14 2.986 1.180 4.095 3.132 3.987 3.880 3.526 1.460 4.885 job15 4.163 3.441 1.217 2.941 1.210 3.794 1.779 1.904 4.255 + job10 job11 job12 job13 job14 job15 initial 3.356 4.324 1.923 3.663 4.103 2.215 job1 2.855 2.653 1.471 2.257 1.186 2.354 job2 1.346 1.410 3.565 3.181 1.126 4.169 job3 2.435 1.972 1.986 1.522 4.734 2.520 job4 1.605 1.697 2.323 2.268 2.288 4.856 job5 3.305 1.206 1.024 2.605 3.080 3.516 job6 2.074 4.793 1.756 2.190 1.298 2.605 job7 4.783 3.386 3.429 2.450 3.376 3.719 job8 4.730 1.805 2.189 1.789 1.985 3.586 job9 3.782 4.383 3.451 4.904 1.108 1.750 job10 3.175 2.805 4.901 1.735 1.654 job11 2.342 2.037 3.563 1.621 2.840 job12 3.288 2.335 4.066 1.440 4.979 job13 3.374 1.138 4.367 3.032 2.198 job14 3.827 4.945 4.419 3.486 3.804 job15 4.967 4.003 3.873 1.002 2.055 ---- 26 PARAMETER due due date job3 28.569, job5 98.104, job6 27.644, job7 55.274, job8 57.364, job11 60.875, job12 96.637 job13 77.888 ---- 26 PARAMETER release release time job5 19.380, job8 48.657, job10 27.932, job13 24.876 ---- 26 SET prec precedence restrictions job3 job1 YES job2 YES
Some jobs have release and due dates. The precedence restrictions say we need to do job 1 and 2 before job 3. The setup times are displayed as a matrix: \(\mathit{setup}_{i,j}\) is the setup time between jobs \(i\) and \(j\). Notice the extra row "initial" which is the last job from the previous planning period. The diagonal elements \(\mathit{setup}_{i,i}\) are not used.
Model
To model this, I use five sets of variables:
| Variable | Description |
|---|---|
| \(\color{DarkRed}{\mathit{First}}_j \in \{0,1\}\) | indicates the first job |
| \(\color{DarkRed}{\mathit{Last}}_j \in \{0,1\}\) | the last job |
| \(\color{DarkRed}{X}_{i,j} \in \{0,1\}\) | job \(j\) immediately follows job \(i\) |
| \(\color{DarkRed}{\mathit{StartTime}}_j \ge 0\) | the start time (after setup) of job \(j\) |
| \(\color{DarkRed}{\mathit{LastTime}}\) | Objective variable: completion time of last job |
The idea is that a job sequence \(1-2-3\) is encoded as:
- \(\color{DarkRed}{\mathit{First}}_1=1\)
- \(\color{DarkRed}{X}_{1,2}=\color{DarkRed}{X}_{2,3}=1\)
- \(\color{DarkRed}{\mathit{Last}}_3=1\)
The model itself looks like:
| No | Equation | Description |
|---|---|---|
| 1 | \[\min \color{DarkRed}{\mathit{LastTime}}\] | objective |
| 2 | \[\sum_j \color{DarkRed}{\mathit{First}}_j = 1\] | exactly one first job |
| 3 | \[\sum_j \color{DarkRed}{\mathit{Last}}_j = 1\] | exactly one last job |
| 4 | \[\color{DarkRed}{\mathit{Last}}_i+\sum_{j\ne i} \color{DarkRed}{X}_{i,j} = 1\>\>\forall i\] | job \(i\) is the last job or it has a successor \(j\) |
| 5 | \[\color{DarkRed}{\mathit{First}}_j+\sum_{i\ne j} \color{DarkRed}{X}_{i,j} = 1\>\>\forall j\] | job \(j\) is the first job or it has a predecessor \(i\) |
| 6 | \[\color{DarkRed}{\mathit{StartTime}}_j \ge \color{DarkBlue}{\mathit{setup}}_{\text{initial},j} \color{DarkRed}{\mathit{First}}_j \>\>\forall j\] | calculate start time of first job |
| 7 | \[\color{DarkRed}{\mathit{StartTime}}_j \ge \color{DarkRed}{\mathit{StartTime}}_i + \color{DarkBlue}{\mathit{proctime}}_i + \color{DarkBlue}{\mathit{setup}}_{i,j} - M(1-\color{DarkRed}{X}_{i,j})\>\>\forall i\ne j\] | calculate start time of job \(j\) with predecessor \(i\) |
| 8 | \[\color{DarkRed}{\mathit{LastTime}} \ge \color{DarkRed}{\mathit{StartTime}}_j + \color{DarkBlue}{\mathit{proctime}}_j\>\>\forall j\] | calculate completion time of last job |
| 9 | \[\color{DarkRed}{\mathit{StartTime}}_j \ge \color{DarkBlue}{\mathit{release}}_j \>\>\forall j \] | lower bound on start time |
| 10 | \[\color{DarkRed}{\mathit{StartTime}}_j \le \color{DarkBlue}{\mathit{due}}_j - \color{DarkBlue}{\mathit{proctime}}_j \>\>\forall j|\color{DarkBlue}{\mathit{due}}_j>0 \] | upper bound on start time |
| 11 | \[ \color{DarkRed}{\mathit{StartTime}}_j \ge \color{DarkRed}{\mathit{StartTime}}_i + \color{DarkBlue}{\mathit{proctime}}_i \>\> \forall \color{DarkBlue}{\mathit{prec}}_{i,j}\] | precedence constraints |
In the above model I have color coded the identifiers: the variables are in red and the parameters are blue.
The big-M constant in constraint 7 was estimated by taking all processing times and adding up the largest setup times. This gives a bound on the total time we need.
Although a bit hidden from sight, this is essentially a Traveling Salesman Problem (TSP). The main issue with TSP formulations is to prevent subtours. A well-known form of subtour-elimination constraints is the Miller, Tucker, Zemlin approach [3]:
| TSP Model using MTZ formulation |
|---|
| \[\begin{align}\min & \sum_{i\ne j} c_{i,j} x_{i,j}\\ & \sum_{j\ne i} x_{i,j} = 1 &&\forall i\\ & \sum_{i\ne j} x_{i,j} = 1 &&\forall j\\ & u_i -u_j + n x_{i,j}\le n-1 && i\ne j, i,j>1\\& x_{i,j} \in \{0,1\}, u_i \ge 0 \end{align}\] |
The subtour elimination constraints can be rearranged as \[ u_j \ge u_i + 1 - n(1-x_{i,j}) \] This is now very much like equation 7.
Having explained why our formulation works, it is also clear we should not expect stellar performance. The MTZ formulation for the TSP problem is known to be rather weak. It is not surprising that scheduling models with complicated setup times are often approached with (meta) heuristics to find good solutions instead of aiming for some form of optimality.
Solution
The example data set with just \(N=15\) jobs is difficult to solve to proven optimality (takes about 3000 seconds). As usual the MIP solver finds good solutions quickly, so we can stop early if we want.
The problem itself is very small:
MODEL STATISTICS BLOCKS OF EQUATIONS 9 SINGLE EQUATIONS 275 BLOCKS OF VARIABLES 6 SINGLE VARIABLES 257 4 projected NON ZERO ELEMENTS 1,176 DISCRETE VARIABLES 240
Models of this size usually solve to optimality within minutes. Clearly MIP solvers perform quite poorly here. The solution looks like:
---- 79 VARIABLE first.L first job job6 1.000 ---- 79 VARIABLE last.L last job job14 1.000 ---- 79 VARIABLE x.L sequencing job1 job2 job3 job4 job5 job7 job8 job9 job10 job1 1.000 job2 1.000 job4 1.000 job6 1.000 job7 1.000 job10 1.000 job11 1.000 job12 1.000 job15 1.000 + job11 job12 job13 job14 job15 job3 1.000 job5 1.000 job8 1.000 job9 1.000 job13 1.000 ---- 79 VARIABLE starttime.L start of job (after setup) job1 18.430, job2 8.112, job3 22.616, job4 88.083, job5 74.658, job6 2.511 job7 43.329, job8 48.657, job9 102.035, job10 93.399, job11 32.238, job12 79.312 job13 59.153, job14 104.746, job15 71.271 ---- 79 VARIABLE lasttime.L = 112.607 last completion time
We can depict the solution as:
 |
| Setup and processing for each job |
Each bar has two parts: the orange part indicates setup and the grey section is processing. Note again that the processing time is constant but the setup times depend on what has happened before. We see that jobs 1 and 2 are indeed processed before job 3. Jobs 3 and 6 have early due dates and we see they are processed early.
The MIP bounds are:
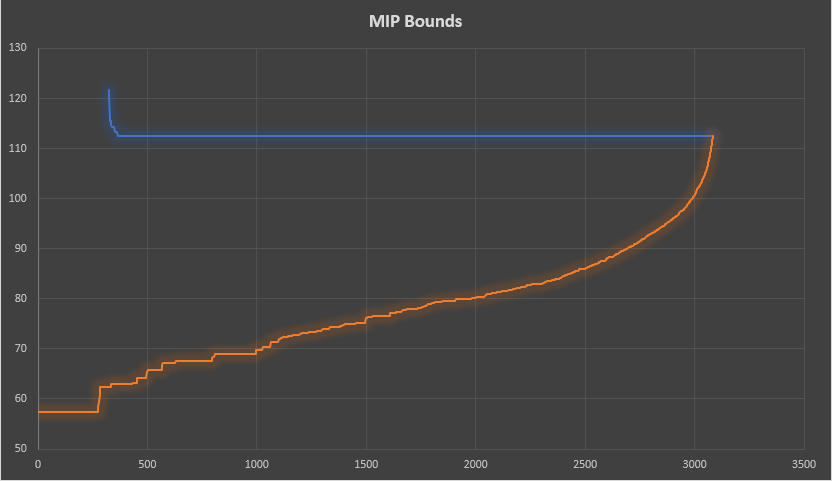 |
| Lower and upper bound. The upper bound is the best found solution. |
When we look at the blue line (best solution so far) we see that the solver had to do a bit of work to find a feasible integer solution. The first feasible solution was found after about 300 seconds. After that the objective quickly improved. After about 500 seconds not much was happening anymore: the solver just worked on tightening the lower bound (the best possible integer solution).
TSP relaxation
Note that if we drop the bounds related to the due and release dates and also ignore the precedence constraints, we end up with a pure TSP model. The TSP cost matrix looks like: \(c_{i,j} = \mathit{setup}_{i,j} + \mathit{proctime}_j\). The cost from the last job back to the initial job is set to zero. As expected this leads to a shorter makespan of 102.595:
 |
| Relaxed TSP solution |
The orange setup times are shorter than for the original model. Of course, as the processing times are constant, we might as well use for TSP costs: \(c_{i,j} = \mathit{setup}_{i,j}\). The optimal objective value will no longer be the total makespan but the optimal sequencing will be the same.
Solving this pure TSP model with TMZ formulation is very difficult and takes much more time than the 3000 seconds we needed for the scheduling model with the additional due date, release date and precedence constraints. These extra constraints make the problem easier (which is not that surprising). To be complete: I solved the TSP model using a very different formulation from [4] (this solved very quickly for this size).
Or-tools
A very fast way of solving this model is presented in [5]. Some notes:
- The fractional values have been scaled to make them integers. In most cases constraint solvers do not like floating point numbers. We may need to watch out for the integer range (some solver may support bigints).
- Preprocessing has been done to move parts of the setup time into the processing time. I.e. \[\begin{align} &\mathit{fixed}_j := \min_i \mathit{setup}_{i,j} \\ & \mathit{proctime}_j := \mathit{proctime}_j + {fixed}_j \\ & \mathit{setup}_{i,j} := \mathit{setup}_{i,j} - {fixed}_j\end{align}\]
References
- A. P. Burger, C. G. Jacobs, J. H. Vuuren, S. E. Visagie, Scheduling Multi-colour Print Jobs with Sequence-dependent Setup Times, J. of Scheduling, vol. 18, no. 2, 2015, pp. 131-14
- Orman, A. J. and Williams, H. Paul (2004) A survey of different integer programming formulations of the travelling salesman problem. Operational Research working papers, LSEOR 04.67
- Miller C.E., A.W. Tucker and R.A. Zemlin (1960) Integer programming formulation of travelling salesman problems, J. ACM, 3, 326–329.
- Unjust benchmark: TSP MIP/Gurobi vs GA/Octave, https://yetanothermathprogrammingconsultant.blogspot.com/2009/04/unjust-benchmark-tsp-mipgurobi-vs.html
- https://github.com/google/or-tools/blob/master/examples/python/single_machine_scheduling_with_setup_release_due_dates_sat.py
Hi Erwin, thank you for your formulation. I have a quastion about sequence dependency. Why did you use TSP formulation. Does not a formulation as below work? SETUP_ij + START_j + PROCESSTİME_j <= M*Xij or SETUP_ij + START_j + PROCESSTİME_j <= M*(1-Xij).
ReplyDeleteThat does not look correct at all.
DeleteSorry, I made a mistake. It is exactly as follows.
DeleteSETUP_ij + START_j + PROCESSTİME_j <= START_i + M*Xij or SETUP_ij + START_j + PROCESSTİME_j <= START_i + M*(1-Xij).
Sorry again, correct formulation is as follows. Let's say setup times are symetric.
DeleteSETUP_ij + START_j + PROCESSTİME_j <= START_i + M*Xij or SETUP_ij + START_i + PROCESSTİME_i <= START_j + M*(1-Xij).
Is'nt this formulation sufficient? Why did you use TSP formulation for setup times?
Dear Erwin, do you have any example for solving similar problem on multiple machine with job exclusions?
ReplyDeleteOur problem is just like the combination of this and another problem you have shared in another article. (https://yetanothermathprogrammingconsultant.blogspot.com/2019/06/machine-scheduling.html)
constraints:
Not all machines can do all jobs
Sequence Dependent Setup Times
object: minimize makespan or overall setup time
thank you so much.